-
Notifications
You must be signed in to change notification settings - Fork 15
Basic workflow
[See associated video]
This will take you through the standard way that the along-tract-stats tools are linked together. This page is an online version of the TrackVis/MATLAB Integration Demo that is included in the html directory when you download along-tract-stats.
Point MATLAB to the directory where the example data are stored. Replace the path here according to your own setup.
exDir = '/path/to/along-tract-stats/example';Set paths to the .trk tract group file and the .nii.gz scalar MRI volume (e.g. FA map).
subDir = fullfile(exDir, 'subject1');
trkPath = fullfile(subDir, 'CST_L.trk');
volPath = fullfile(subDir, 'dti_fa.nii.gz');Read in the scalar FA map with FSL tools. (See $FSLDIR/etc/matlab)
volume = read_avw(volPath);Read in the .trk file. You will get a header structure with fields from the .trk header, and a tracks structure array with an element for each streamline in the tract group.
[header tracks] = trk_read(trkPath)Output:
header =
id_string: 'TRACK '
dim: [192 192 55]
voxel_size: [1.2500 1.2500 2.5000]
origin: [0 0 0]
n_scalars: 0
scalar_name: [10x20 char]
n_properties: 0
property_name: [10x20 char]
reserved: [508x1 char]
voxel_order: 'LPS '
pad2: 'LAS '
image_orientation_patient: [1 0 0 0 -1 0]
pad1: ' '
invert_x: 0
invert_y: 1
invert_z: 0
swap_xy: 0
swap_yz: 0
swap_zx: 0
n_count: 734
version: 2
hdr_size: 1000
tracks =
1x734 struct array with fields:
nPoints
matrixEach structure in the tracks array contains fields for the number of points in that particular streamline, and the raw matrix of those points in mm coordinates [nPoints x 3]. If there were any whole-tract properties associated with the tract group, those would be listed here too.
tracks(1)
tracks(1).matrixOutput:
ans =
nPoints: 73
matrix: [73x3 double]
ans =
120.6250 105.6250 1.2500
120.7721 105.9612 2.6684
120.9682 106.2587 4.0910
121.3031 106.5639 5.8192
121.6318 106.9971 7.5074
121.8181 107.5721 8.8092
121.9920 108.3112 10.0386
122.5117 109.9120 12.1337
123.0796 111.1412 13.5634
123.6738 112.3017 15.0360
124.0613 113.0783 16.2544
124.4113 113.7492 17.5483
125.1193 114.7262 20.0167
126.0355 115.4616 22.5005
126.4101 115.7442 23.7574
126.7523 116.0492 25.0180
...Even though these tools are designed for looking at along-tract statistics, functions are stil included for determining the mean values of scalars, like FA, averaged across the whole tract. When setting up your workflow, it is useful to check these values to make sure they agree with what is reported in the tracking program (e.g. TrackVis). If they aren’t close, there is likely some orientation or related issue that needs to be worked out.
Determine traditional statistics collapsed across the whole tract.
[meanInt stdInt nVox] = trk_stats(header, tracks, volume, 'nearest')Output:
Warning: Tracks don't have same length; padded with NaNs.
meanInt =
0.5863
stdInt =
0.1370
nVox =
1777You can also look at streamline length.
lengths = trk_length(tracks);
mean(lengths)
std(lengths)Output:
ans =
121.7951
ans =
13.1734In order to look at FA along the tract, we first resample the streamlines so that they all have the same number of vertices spread evenly along their lengths. (However, see tie-at-center for a slightly more complex option that is usually preferable.) Here we use cubic B-spline interpolation and prescribe that we want 100 vertices in each streamline:
tracks_interp = trk_interp(tracks, 100);Since the output of trk_interp is in matrix form (type help trk_interp to see this), we reformat the tracks back into a structure form.
tracks_interp_str = trk_restruc(tracks_interp);Now we plot the tract group. The last input argument indicates the slice planes for volume overlays. Red markers indicate starting points. Note the random ordering of tracks, with some “starting” in the cortex and some in the brainstem.
figure, trk_plot(header, tracks_interp_str, volume, [95 78 4])
view([30 30])
Since the default ordering of vertices within streamlines is arbitrary, we must flip some of the streamlines so that they all “start” at the same end of the tract. For some tracts, it is sufficient to specify a coordinate near the desired origin. For others (e.g. arcuate fasciculus, forceps major/minor, etc.), it is better to pick the origin manually for each subject. Since the corticospinal tract is pretty long, here we’ll specify a point near the brainstem. If we don’t provide a coordinate, the origin will be determined interactively [See video].
tracks_interp = trk_flip(header, tracks_interp, [97 110 4]);
tracks_interp_str = trk_restruc(tracks_interp);Plot the streamlines again to see that they have all been reordered.
figure, trk_plot(header, tracks_interp_str, volume, [95 78 4])
view([30 30])
For each point along the streamlines in tracks_interp_str, we extract the corresponding voxel intensity from volume.
[header_sc tracks_sc] = trk_add_sc(header, tracks_interp_str, volume, 'FA');Obtain the mean FA at the different “cross-sections” along the curving tract spine.
[scalar_mean scalar_sd] = trk_mean_sc(header_sc, tracks_sc);Finally, make a basic MATLAB plot of the mean FA value ± SD along the tract.
figure, hold on
plot(scalar_mean, 'k')
plot(scalar_mean+scalar_sd, 'k--')
plot(scalar_mean-scalar_sd, 'k--')
% Make the plot prettier
hold off, box off
xlim([0 100]), ylim([0 1])
title('\bf{Mean FA along track}')
xlabel('Distance along track (%)')
ylabel('Fractional Anisotropy (FA)')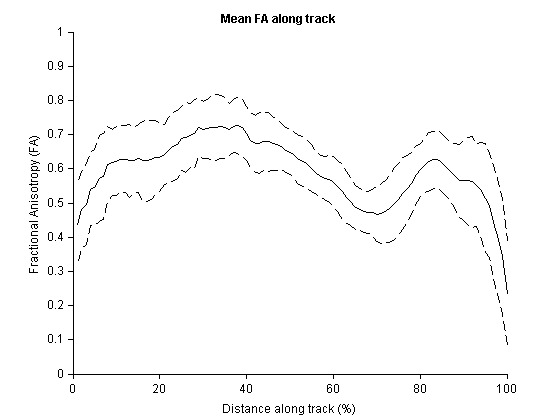
The mean streamline geometry (i.e. one streamline that represents the mean of all the original streamlines) can also be calculated.
track_mean = mean(tracks_interp, 3);This average geometry can now be packaged up with the mean scalar values.
- Multiple scalars are allowed by the .trk format, which is very nice because it means we can also tag the vertices with other data like statistical significance values.
- A dummy streamline should be added with the desired display ranges for the scalars, if these exceed the ranges in the data (e.g. if you want the color bar for FA to be [0,1] even though the real data doesn’t fill that range).
track_mean_sc = [track_mean scalar_mean];
% x y z sc1
track_mean_sc(1:2,:,2) = [0 0 0 0; %min
0 0 0.1 1]; %max
track_mean_sc_str = trk_restruc(track_mean_sc);The header must be updated because now we only have 1 streamline (plus the 1 dummy range streamline) instead of many.
header_mean_sc = header_sc;
header_mean_sc.n_count = 2;Lastly, our results can be exported back out to a .trk file for visualization in TrackVis (this output is included in the example folder).
savePath = fullfile(exDir, 'CST_L_mean.trk');
trk_write(header_mean_sc, track_mean_sc_str, savePath)Here we display the mean corticospinal tract geometry from the example subject, overlaid with the along-tract variation in FA [See video].
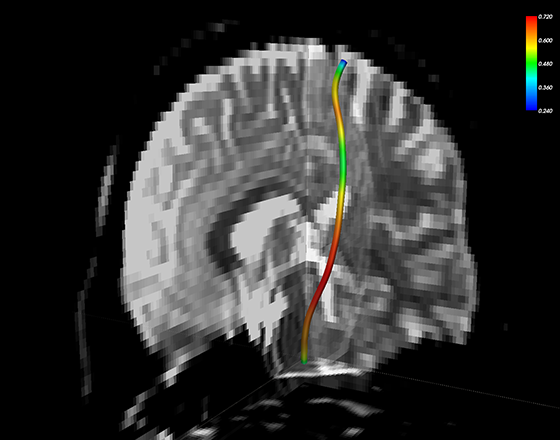
Back to Wiki Home