Skip to content

LIP0015

Jump to bottom Edit New page
Jos van de Wolfshaar edited this page Apr 12, 2018 · 2 revisions

LIP 15 - Dynamic SPNs

LIP 15
Title Dynamic SPNs
Author J. van de Wolfshaar
Status Draft
Type Standard
Discussion Issue #47
PR
Created April 12, 2018

Introduction

Dynamic SPNs were introduced as a way to learn tractable probabilistic models on sequential data. They extend on single-step SPNs similar to the way dynamic Bayesian nets are a sequence-aware extension of Bayesian nets. For further reference, one can consult Dynamic Sum Product Networks for Tractable Inference on Sequence Data by Melibari, Poupart, Doshi and Trimponias (2016), available here. An extended version of the paper can be found here.

Branch devoted to this LIP can be found here.

Technical Background

In the case of a dynamic SPN, we repeat the set of input variables multiple times, i.e.:

{[X_1,...,X_N]^1,[X_1,...,X_N]^2,...,[X_1,...,X_N]^T}

where N is the total number of variables per step and T is the total number of steps.

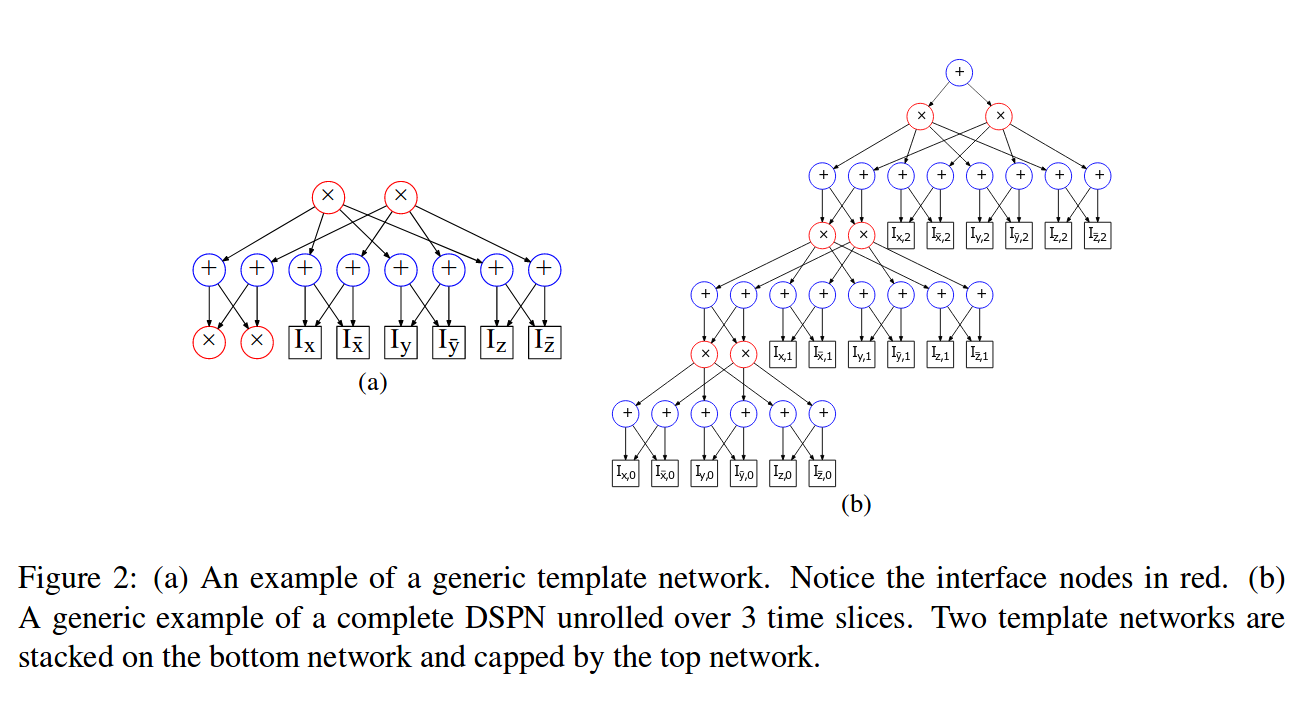
Dynamic SPNs are valid by inducing the following restriction on their structure. I.e. they are built up out of three components:

  1. A template network for a slice of N variables at time t, a directed acyclic graph with k roots and k + 2n leaf nodes (if binary variables). The 2n variables are given by [X_1,~X_1,...,X_N,~X_N]^t, while the remaining k leaves are interface nodes. The interface nodes are used to pass on information from previous time steps.
  2. A bottom network for the first slice of variables (t==1). This also as k roots, but only 2n leafs. The k roots are interface nodes to the template network for the next slice
  3. A top network, again a directed acyclic graph composed of sums and products. Has k leafs that are interfaces to the template network applied to the last time slice.

For more information on the exact restrictions for each of these components, one can refer to the paper.

Proposal

Ideally, LibSPN supports building dynamic SPNs with little intervention of dynamic components during graph definition. One occasion where we at least have to make a difference is when defining the input to the graph, e.g. a VarNode. When building dynamic SPNs the VarNodes should have tf.placeholder with rank 3, instead of rank 2. For reasons of simplicity and efficiency, the first axis 0 will represent time (commonly referred to as time-major). Having the first axis as time allows us to unstack the tensor into a TensorArray and start querying the array accordingly for different moments in time.

Note that the core operations are built through traversing the graph either with compute_graph_up or compute_graph_up_down in algorithms.py. The least intrusive way to enable dynamic SPN construction is to provide dynamic counterparts of these functions as well as explicitly defining DynamicVarNodes that handle the time dimension properly. Put briefly, this LIP involves:

  • Defining compute_graph_up_dynamic and compute_graph_up_down_dynamic that are sequence-aware.
  • Defining DynamicVarNode and its dynamic descendants DynamicIVs and DynamicContVars.
  • Defining an DynamicInterface (inherits from Node) of which the value at time t is given by some source node at time t-1.
  • Value and LogValue should be aware of time
  • MPE path construction should be aware of time
  • MPE state construction should be aware of time
  • For ease of use and development, we'll assume that the bottom network has the same structure as the template network. The information coming from the previous time step for the bottom network (from time t == -1) will then be 'marginalized' out by setting the output of any interface_head to be 1 when t == 0.

Usage example

Currently, the implementation provides the following semantics:

max_steps = 4

# Define sequence-aware inputs
ix = spn.DynamicIVs(name="iv_x", num_vars=1, num_vals=2, max_steps=max_steps)
iy = spn.DynamicIVs(name="iv_y", num_vars=1, num_vals=2, max_steps=max_steps)
iz = spn.DynamicIVs(name="iv_z", num_vars=1, num_vals=2, max_steps=max_steps)

# First define template network
mix_x0 = spn.Sum(ix, name="mixture_x0")
mix_x1 = spn.Sum(ix, name="mixture_x1")
mix_y0 = spn.Sum(iy, name="mixture_y0")
mix_y1 = spn.Sum(iy, name="mixture_y1")
mix_z0 = spn.Sum(iz, name="mixture_z0")
mix_z1 = spn.Sum(iz, name="mixture_z1")

# Define interface network
intf0 = spn.DynamicInterface(name="interface0")
intf1 = spn.DynamicInterface(name="interface1")

mix_int0 = spn.Sum(intf0, intf1, name="mixture_intf0", interface_head=True)
mix_int1 = spn.Sum(intf0, intf1, name="mixture_intf1", interface_head=True)

# Define template heads
prod0 = spn.Product(mix_x0, mix_y0, mix_z0, mix_int0, name="prod0")
prod1 = spn.Product(mix_x1, mix_y1, mix_z1, mix_int1, name="prod1")

# Register sources for interface nodes
intf0.set_source(prod0)
intf1.set_source(prod1)

# Define top network
top_net = spn.Sum(prod0, prod1, name="top")

spn.generate_weights(root=top_net, init_value=1)

dval = spn.DynamicValue(spn.InferenceType.MARGINAL)
val_op, val_per_step = dval.get_value(top_net, return_sequence=True)

dlogval = spn.DynamicLogValue(spn.InferenceType.MARGINAL)
val_op, val_per_step = dlogval.get_value(top_net, return_sequence=True)

init = spn.initialize_weights(top_net)

This implementation realizes 4 steps of the network displayed in the image below, which is taken from the paper.

Dynamic SPN

As you can see, these semantics don't alter the behavior for Sum and Product nodes in any way. However, each node has some additional properties, such as interface_head that are set at instantiation. At the current setup, it is not inferred automatically when a node is the 'head' of an interface, but this might be inferred automatically in a future implementation.

Other than that, the DynamicInterface has been added. As you can see, it is defined before its source can be set. Usually that is because the head of the template network also needs to have information from the interface. In this example, the nodes prod0 and prod1 are sources for intf0 and intf1, respectively.

The flag return_sequences can be set to also provide an outcome per step if desired, similar to the way tf.nn.dynamic_rnn provides a return_sequences flag.

A more advanced example combines the dense generator with the dynamic semantics for binarized MNIST generative training on two different digits, where each row of the image is seen as a time slice.

ivs = spn.DynamicIVs(num_vars=14, num_vals=2, max_steps=14)
dense_gen = spn.DenseSPNGenerator(num_decomps=num_decomps, num_subsets=num_subsets, num_mixtures=num_mixtures, 
                                  input_dist=input_dist, 
                                  num_input_mixtures=num_input_mixtures)

# Generate a dense template network
dense0 = dense_gen.generate(ivs)
interface0 = spn.DynamicInterface(name="interface0", interface_head=True)
prod0 = spn.Product(dense0, interface0, name="Prod0")
interface0.set_source(prod0)

# Generate another dense template network
dense1 = dense_gen.generate(ivs)
interface1 = spn.DynamicInterface(name="interface1")
prod1 = spn.Product(dense1, interface1, name="Prod1", interface_head=True)
interface1.set_source(prod1)

# Finally combine the two dynamic SPNs in top network
root = spn.Sum(prod0, prod1)

spn.generate_weights(root, init_value=weight_init_value)
latent = root.generate_ivs()

Although the above architecture isn't effective for modeling the two digits, it nicely demonstrates the flexibility of the proposed approach.

Extensions

  • Determine automatically when a node is an interface_head.
  • Add flag to support both time major and batch major to conf.

Decision

Add a custom footer
Add a custom sidebar
Clone this wiki locally