LIP0008

LIP 8 - Revising the IV value construction

LIP	8
Title	Revising the IV value construction
Author	J. van de Wolfshaar
Status	Draft
Type	Standard
Discussion	Issue #38
PR
Created	Feb 22, 2018

Introduction

As became apparent during several performance tests, the value of IVs nodes can take a considerable amount of wall time compared to other parts of graph. In this LIP, we will propose an alternative implementation of the sub graph that computes the value of the IVs from the sparse input representation.

Technical Background

At this point, the value of an IV is computed as follows:

def _compute_value(self):
    """Assemble the TF operations computing the output value of the node
    for a normal upwards pass.

    This function converts the integer inputs to indicators.

    Returns:
        Tensor: A tensor of shape ``[None, num_vars*num_vals]``, where the
        first dimension corresponds to the batch size.
    """
    # The output type has to be conf.dtype otherwise MatMul will
    # complain about being unable to mix types
    oh = tf.one_hot(self._feed, self._num_vals, dtype=conf.dtype)
    # Detect negative input values and convert them to all IVs equal to 1
    neg = tf.expand_dims(tf.cast(tf.less(self._feed, 0), dtype=conf.dtype), dim=-1)
    oh = tf.add(oh, neg)
    # Reshape
    return tf.reshape(oh, [-1, self._num_vars * self._num_vals])

And its log value (in VarNode) is defined as:

def _compute_log_value(self):
    """Assemble TF operations computing the marginal log value of this node.

    Returns:
        Tensor: A tensor of shape ``[None, out_size]``, where the first
        dimension corresponds to the batch size.
    """
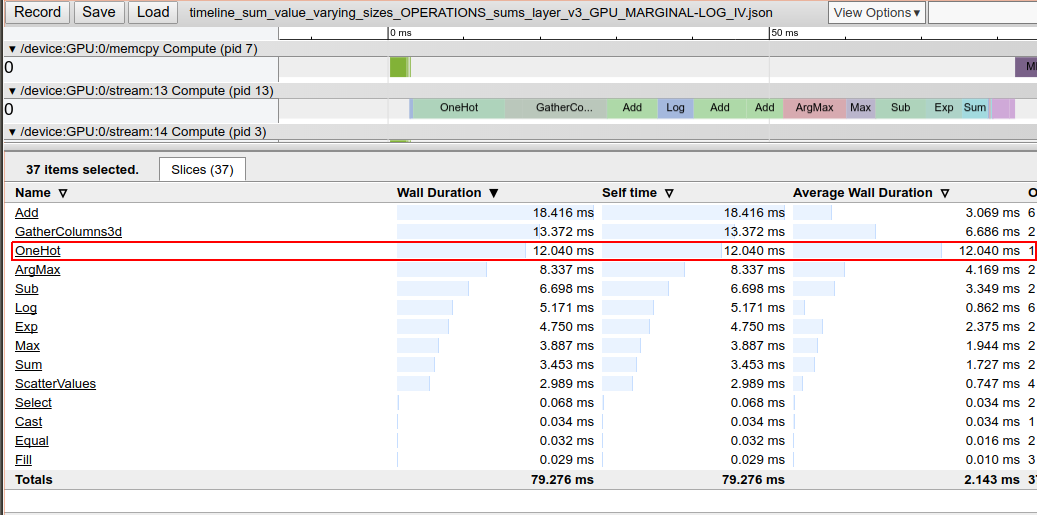
    return tf.log(self._compute_value())

When using IVs with a large number of sums, this part of the code can become one of the most expensive to compute as can be seen in the image below (taken from a performance test profiling of a SumsLayer):

Proposal

We could actually reduce the graph size and simplify the implementation of the _compute_value by storing every possible row of the resulting tensor in advance and then gathering the correct indices. If our _feed is actually a sparse representation of IVs then we might just use the value of _feed as row indices of an identity matrix as large as self._num_vals. We could even reuse a single identity matrix for any IV in our graph. This would then be an identity matrix of the maximum self._num_vals size over all IVs instances. The value of the IV can then be found using tf.gather on the identity matrix.

Of course, we need to take care of the inputs with the value -1. We could realize that by adding another row to the top of the matrix and the adding 1 to the values before calling tf.gather.

Lastly, for the _compute_log_value we should predefine the log of the matrix described above, so that we don't need to perform tf.log afterwards and simply gather instead.

Performance comparison

The overview below displays the performance differences when using gather vs. one_hot. There is a marginal speed up in the case of the gather alternatives. The gather_v1 implementation uses a tf.constant to store the identity matrix and the gather_v2 implementation uses a tf.Variable to store the matrix. Finally, the gather_v3 uses a single matrix to store identity matrix for all IVs in the graph (in this case we model the value computation of 10 IV nodes with a batch size of 60000 and 200 values each).

#-----------------------#
IVs value
#-----------------------#
CPU          op    dt:  size  setup_time  first_run_time  rest_run_time    correct
GPU          op    dt:  size  setup_time  first_run_time  rest_run_time    correct
      gather_v1 int32:    54       19.03            5.77           1.00       True
      gather_v2 int32:    69       26.48            3.65           1.06       True
      gather_v3 int32:    34       13.74            5.41           0.96       True
        one_hot int32:    64       21.73           13.52           1.26       True

#-----------------------#
IVs log value
#-----------------------#
CPU          op    dt:  size  setup_time  first_run_time  rest_run_time    correct
GPU          op    dt:  size  setup_time  first_run_time  rest_run_time    correct
      gather_v1 int32:    59       29.34            7.78           1.04       True
      gather_v2 int32:    74       34.57            4.50           1.08       True
      gather_v3 int32:    35       15.40            5.67           1.06       True
        one_hot int32:    69       22.38            6.47           1.22       True

Decision

In principle, constructing a dense one-hot representation should still be faster than simply gathering from an identity matrix as this requires full memory copying per row, instead of just initializing memory at 0 and inserting 1 at a limited set of rows.

This suggests that the TF implementation is not implemented efficiently. Another LIP will propose a custom TF operation for IVs that deals with the dense representation.