Home

HAllA Overview

Given two high-dimensional 'omics datasets X and Y (continuous and/or categorical features) from the same n biosamples, HAllA (Hierarchical All-against-All Association Testing) discovers densely-associated blocks of features in the X vs. Y association matrix where:

• each block is defined as all associations between features in a subtree of X hierarchy and features in a subtree of Y hierarchy,
• and a block is densely associated if (1 - FNR)% of pairwise associations are FDR significant (FNR is the pre-defined expected false negative rate)

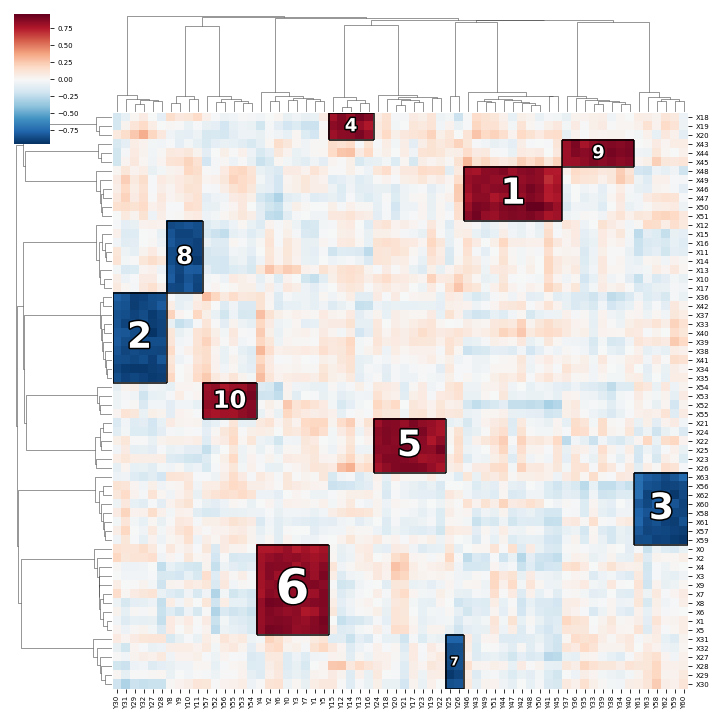
There are three steps in HAllA:

1. Computing pairwise similarity matrix between all features in X and Y
2. Hierarchical clustering of features in X and Y separately
3. Finding densely-associated blocks iteratively

1. Pairwise similarity matrix computation

The pairwise similarity matrix between all features in X and Y is computed with a specified similarity measure, such as Spearman correlation and normalized mutual information (NMI). This step then generates the p-value and q-value tables.

Note that for handling heterogeneous data, all continuous features are first discretized into bins using a specified binning method.

2. Hierarchical clustering

Hierarchical clustering on the features in each dataset is performed using the converted similarity measure used in step 1. It produces a tree for each dataset.

3. Finding densely-associated blocks

This recursive step is described in the pseudocode below:

def find_densely_associated_blocks(x, y):
    x_features = all features in x
    y_features = all features in y
    if is_densely_associated(x_features, y_features):
        report block and terminate
    else:
        # bifurcate one according to Gini impurities of the splits
        x_branches, y_branches = bifurcate_one_of(x, y)
        if both x and y are leaves:
            terminate
        for each x_branch and y_branch in x_branches and y_branches:
            find_densely_associated_blocks(x_branch, y_branch)

initial function call: find_densely_associated_blocks(X_root, Y_root)

For example, given two datasets of X (features: X1, X2, X3, X4, X5) and Y (features: Y1, Y2, Y3, Y4) both hierarchically clustered in X tree and Y tree, the algorithm first evaluates the roots of both trees and checks if the block consisting of all features of X and Y are densely-associated (if %significance (%reject) >= (1 - FNR)%).

If the block is not densely-associated, the algorithm would bifurcate one of the trees. It would pick one of:

• [X1 X2][X3 X4 X5] >< [Y1 Y2 Y3 Y4] or
• [X1 X2 X3 X4 X5] >< [Y1 Y2 Y3][Y4]

based on the Gini impurity of the splits (pick the split that produces a lower weighted Gini impurity),

Once it picks the split with the lower impurity (let's say the first split), it will iteratively evaluate the branches:

• find densely-associated blocks in [X1 X2] vs [Y1 Y2 Y3 Y4], and
• find densely-associated blocks in [X3 X4 X5] vs [Y1 Y2 Y3 Y4]

and keep going until it terminates.