Short Truth Table Rules
Short Truth Table is a visual representation of logic expressions for which you need to assign values in the Short Truth Table Method.
The Short Truth Table Method assigns truth values to the involved atomic and complex statements in order to obtain a desired combination of truth values. The Short Truth Table Method thus tries to generate one row of the truth table that has the combination of truth values in which you are interested. The Truth Table Method systematically exhausts all possible truth value combinations of the involved statements. In the truth table, we look for a row that reflects a certain possibility, and that will tell us the answer to whatever question we had. The Short Truth Table Method shortens this process by focusing the search.
As you assign truth values to certain statements, the truth values of other statements can be forced. For example, if you are forced to make a statement both true and false, then you know that the combination of truth values you are looking for does not exist (this is called Contradiction, and you can see its rules in later sections, as well as other rules that will help you solve given exercises). The Short Truth Table Method is therefore often a kind of proof by contradiction or indirect proof.
There are different final evaluations of logical arguments (collections of premises and conclusions) that you can reach as a result of the Short Truth Table Method:
- Valid Argument: It is not possible to have true premises and a false conclusion. To prove this, you can suppose the premises of an argument are true and the conclusion is false, and derive a contradiction.
- Invalid Argument: It is possible to have true premises and a false conclusion. To prove this, you can suppose the premises of an argument are true and the conclusion is false, and that all statements can be evaluated in that case with no contradictions.
- Tautology: It is not possible for the statement in question to be false. To prove this, you can suppose the statement in question is false and derive a contradiction.
- Contradiction: It is not possible for the statement to be true. To prove this, you can suppose the statement in question is true and derive a contradiction (which, in this sense, means that if the statement is true then some other statement or variable is assigned both true and false according to the Contradiction Rules later on).
In LEGUP Short Truth Table, rather than annotating statements with truth values, we’ll turn the statements green (True) or red (False). The truth value of a statement is indicated by the truth value of its outermost operator. The truth values of operators and variables are linked to one another according to the rules in the following sections.
In order to complete a proof in this Puzzle, you will change the undetermined truth values of each block in each statement in a systematic way, supporting each change with a logical rule from the list below. The truth values of the blocks can be changed in the following ways:
- Clicking on a gray block will color it green (True).
- Clicking on a green block will color it red (False).
- Clicking on a red block will color it gray (Undetermined).
For each change in truth value, you will back up your reasoning with one of LEGUP's defined rules, as defined below. At every stage of your solution, LEGUP will keep a visual representation of the proof in the Proof Tree window, with circles representing the stages of the proof. The proof moves along from left to right, with Case Rules causing splits in the tree represented by diverging arrows toward new levels of circles, and with green arrows representing changes that have been supported by a Rule. In order to support a change, you can ensure that you have the correct stage in the Proof Tree selected (the block in question will be bordered in green), and then select the Rule in the Rules window that corresponds to the change you made at that stage.
If you reach a Contradiction in your proof, you can close a Tree branch by selecting the correct Contradiction Rule from the Rules window. Once all branches are closed, or all possible truth values for all blocks have been explored, you can select the Check or Check All buttons to have LEGUP check that your solution and reasoning are correct.
Use this case on a unknown variable to create a split in the branch where the variable is true in one branch, and false in another
Use this case on a known 'Biconditional' to create a split in the branch where the surronding expressions will satisfy the condition
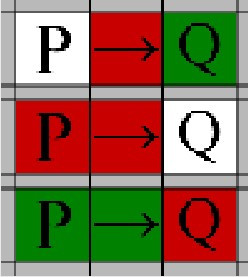
Use this case on a known 'Conditional' to create a split in the branch where the surronding expressions will satisfy the condition
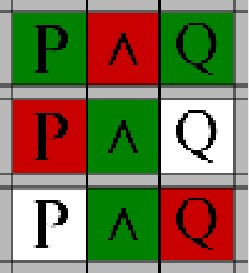
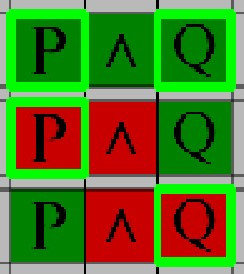
Use this case on a known 'And' to create a split in the branch where the surronding expressions will satisfy the condition
Use this case on a known 'Or' to create a split in the branch where the surronding expressions will satisfy the condition
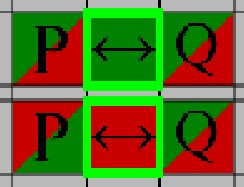
Use this rule to end a line of reasoning if the value of the 'Bicondtional' is incorrect based on the surronding expressions
Use this rule to end a line of reasoning if the value of the 'Condtional' is incorrect based on the surronding expressions
Use this rule to end a line of reasoning if the value of the 'And' is incorrect based on the surronding expressions
Use this rule to end a line of reasoning if the value of the 'Or' is incorrect based on the surronding expressions
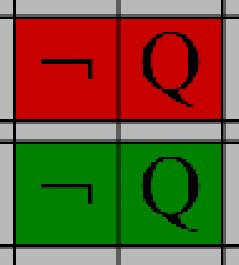
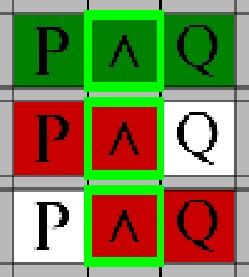
Use this rule to end a line of reasoning if the value of the 'Not' is incorrect based on the surronding expression
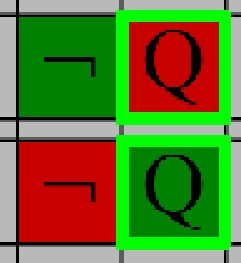
Use this rule to end a line of reasoning if the value a variable in two locations has two different states
The same variable must hold it's truth value in all cases, Use this rule to assign all of a given variable the same value
Use this rule to assign an expression a truth value depending on the 'Biconditional' State
Use this rule to assign an expression a truth value depending on the 'Conditional' State
Use this rule to assign an expression a truth value depending on the 'And' State
Use this rule to color an expression green or red depending on the 'conditional' State
Use this rule to assign an expression a truth value depending on the 'Not' State
Use this rule to Assign the 'Bicontional' a truth value on the the surronding expressions
Use this rule to Assign the 'Condtional' a truth value on the the surronding expressions
Use this rule to Assign the 'And' a truth value on the the surronding expressions
Use this rule to Assign the 'Or' a truth value on the the surronding expressions
Use this rule to Assign the 'Not' a truth value on the the surronding expressions
These are the truth table configurations on which the LEGUP Rules are founded. Every LEGUP Rule logically follows from one or more of these truth tables.
Biconditional (<-->) Expression Truth Table
| Left Expression | Right Expression | Truth State |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | T |
Conditional (-->) Expression Truth Table
| Left Expression | Right Expression | Truth State |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
Conjunction (AND) Expression Truth Table
| Left Expression | Right Expression | Truth State |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
Disjunction (OR) Expression Truth Table
| Left Expression | Right Expression | Truth State |
|---|---|---|
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
Negation (NOT) Expression Truth Table
| Expression | Truth State |
|---|---|
| T | F |
| F | T |