-
Notifications
You must be signed in to change notification settings - Fork 82
Short Truth Table Rules
Short Truth Table is a visual representation of logic expressions for which you need to assign values in the Short Truth Table Method.
The Short Truth Table Method assigns truth values to the involved atomic and complex statements in order to obtain a desired combination of truth values. The Short Truth Table Method thus tries to generate one row of the truth table that has the combination of truth values in which you are interested. The Truth Table Method systematically exhausts all possible truth value combinations of the involved statements. In the truth table, we look for a row that reflects a certain possibility, and that will tell us the answer to whatever question we had. The Short Truth Table Method shortens this process by focusing the search.
As you assign truth values to certain statements, the truth values of other statements can be forced. For example, if you are forced to make a statement both true and false, then you know that the combination of truth values you are looking for does not exist (this is called Contradiction, and you can see its rules in later sections, as well as other rules that will help you solve given exercises). The Short Truth Table Method is therefore often a kind of proof by contradiction or indirect proof.
There are different final evaluations of logical arguments (collections of premises and conclusions) that you can reach as a result of the Short Truth Table Method:
- Valid Argument: It is not possible to have true premises and a false conclusion. To prove this, you can suppose the premises of an argument are true and the conclusion is false, and derive a contradiction.
- Invalid Argument: It is possible to have true premises and a false conclusion. To prove this, you can suppose the premises of an argument are true and the conclusion is false, and that all statements can be evaluated in that case with no contradictions.
- Tautology: It is not possible for the statement in question to be false. To prove this, you can suppose the statement in question is false and derive a contradiction.
- Contradiction: It is not possible for the statement to be true. To prove this, you can suppose the statement in question is true and derive a contradiction (which, in this sense, means that if the statement is true then some other statement or variable is assigned both true and false according to the Contradiction Rules later on).
In LEGUP Short Truth Table, rather than annotating statements with truth values, we’ll turn the statements green (True) or red (False). The truth value of a statement is indicated by the truth value of its outermost operator. The truth values of operators and variables are linked to one another according to the rules in the following sections.
In order to complete a proof in this Puzzle, you will change the undetermined truth values of each block in each statement in a systematic way, supporting each change with a logical rule from the list below. The truth values of the blocks can be changed in the following ways:
- Clicking on a gray block will color it green (True).
- Clicking on a green block will color it red (False).
- Clicking on a red block will color it gray (Undetermined).
For each change in truth value, you will back up your reasoning with one of LEGUP's defined rules, as defined below. At every stage of your solution, LEGUP will keep a visual representation of the proof in the Proof Tree window, with circles representing the stages of the proof. The proof moves along from left to right, with Case Rules causing splits in the tree represented by diverging arrows toward new levels of circles, and with green arrows representing changes that have been supported by a Rule. In order to support a change, you can ensure that you have the correct stage in the Proof Tree selected (the block in question will be bordered in green), and then select the Rule in the Rules window that corresponds to the change you made at that stage. Alternatively, you can select a Rule and then a corresponding block in the statements to automatically create a new node or nodes with that Rule as its foundation.
If you reach a Contradiction in your proof, you can close a Tree branch by selecting the correct Contradiction Rule from the Rules window. Once all branches are closed, or all possible truth values for all blocks have been explored, you can select the Check or Check All buttons to have LEGUP check that your solution and reasoning are correct.
Use this case on a variable of Undetermined truth value to create a split in the current branch of the Tree where the variable is True in one branch, and False in another.
Use this case on a Biconditional operator of known truth value to create a split in the current branch of the Tree where the surrounding expressions will satisfy the condition in different ways in the two new branches.
Use this case on a Conditional operator of known truth value to create a split in the current branch of the Tree where the surrounding expressions will satisfy the condition in different ways in the two new branches.
Use this case on a an AND operator that is known to be False to create a split in the current branch of the Tree where the surrounding expressions will satisfy the condition in different ways in the two new branches.
Use this case on an OR operator that is known to be True to create a split in the current branch of the Tree where the surrounding expressions will satisfy the condition in different ways in the two new branches.
Use this rule to end a line of reasoning if the value of the Biconditional operator is incorrect based on the surrounding expressions. Specifically:
- If both sides of the Biconditional statement are True or False, the Biconditional cannot be False
- If one side of the Biconditional statement is False while the other is True, the Biconditional itself cannot be True
Use this rule to end a line of reasoning if the value of the Conditional operator is incorrect based on the surrounding expressions. Specifically:
- If the right side of the Conditional statement is True, the Conditional cannot be False
- If the left side of the Conditional statement is False, the Conditional cannot be False
- If the right side of the Conditional statement is False while the left side is True, the Conditional itself cannot be True
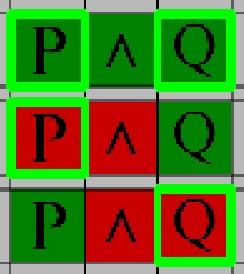
Use this rule to end a line of reasoning if the value of the AND operator is incorrect based on the surrounding expressions. Specifically:
- If both sides of the AND statement are True, the AND itself cannot be False
- If either side of the AND statement is False, the AND itself cannot be True
Use this rule to end a line of reasoning if the value of the OR operator is incorrect based on the surrounding expressions. Specifically:
- If either side of the OR statement is True, the OR itself cannot be False
- If both sides of the OR statement are False, the OR itself cannot be True
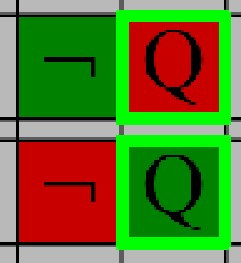
Use this rule to end a line of reasoning if the value of the NOT operator is incorrect based on the surrounding expression. Specifically:
- If the negated variable is False, the NOT cannot be False
- If the negated variable is True, the NOT cannot be True
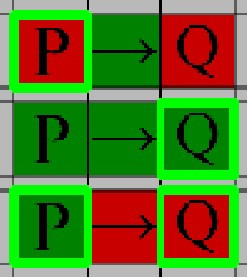
Use this rule to end a line of reasoning if the value a variable in two locations has two different truth values.
The same variable must hold its truth value in all cases. Use this rule to assign all instances of a given variable the same value.
Use this rule to assign an expression in a Biconditional statement a truth value depending on the known truth value of the Biconditional operator. Specifically:
- If the Biconditional is True, the statements on either side must have the same truth value
- If the Biconditional is False, the statements on either side must have different truth values
Use this rule to assign a truth value to an expression in a Conditional statement depending on the truth value of the Conditional operator. Specifically:
- If the Conditional is True and the right side is False, the left side must be False
- If the Conditional is True and the left side is True, the right side must be True
- If the Conditional is False then the left side must be True and the right side must be False
Use this rule to assign a truth value to an expression in an AND statement depending on the truth value of the AND operator. Specifically:
- If the AND is True, both sides must be True
- If the AND is False and the right side is True, the left side must be False, and vice versa
- If the AND is False and the left side is True, the right side must be False, and vice versa
Use this rule to assign a truth value to an expression in an OR statement depending on the truth value of the OR operator. Specifically:
- If the OR is True and the right side is False, the left side must be True, and vice versa
- If the OR is True and the left side is False, the right side must be True, and vice versa
Use this rule to assign a truth value to an expression in a NOT statement depending on the truth value of the NOT operator. Specifically:
- If the NOT is True, the negated expression must be False
- If the NOT is False, the negated expression must be True
Use this rule to assign a truth value to a Biconditional operator depending on the truth value of the surrounding expressions. Specifically:
- If both expressions are either True or False, the Biconditional is True
- If the expressions have different truth values, the Biconditional is False
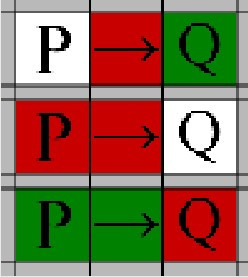
Use this rule to assign a truth value to a Conditional operator depending on the truth value of the surrounding expressions. Specifically:
- If the left side is False, the Conditional is True
- If the right side is True, the Conditional is False
- If the left side is True and the right side is False, the Conditional is False
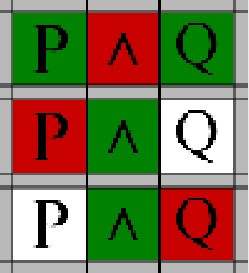
Use this rule to assign a truth value to an AND operator depending on the truth value of the surrounding expressions. Specifically:
- If both expressions are True, the AND is True
- If either expression is False, the AND is False
Use this rule to assign a truth value to an OR operator depending on the truth value of the surrounding expressions. Specifically:
- If either expression is True, the OR is True
- If both expressions are False, the OR is False
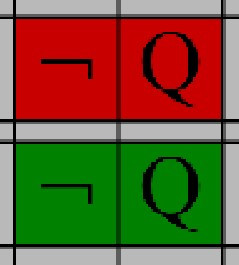
Use this rule to assign a truth value to a NOT operator depending on the truth value of the negated expression. Specifically:
- If the negated expression is False, the NOT is True
- If the negated expression is True, the NOT is False
These are the truth table configurations on which the LEGUP Rules are founded. Every LEGUP Rule logically follows from one or more of these truth tables.
Biconditional (<-->) Expression Truth Table
| Left Expression | Right Expression | Truth State |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | T |
Conditional (-->) Expression Truth Table
| Left Expression | Right Expression | Truth State |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
Conjunction (AND) Expression Truth Table
| Left Expression | Right Expression | Truth State |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
Disjunction (OR) Expression Truth Table
| Left Expression | Right Expression | Truth State |
|---|---|---|
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
Negation (NOT) Expression Truth Table
| Expression | Truth State |
|---|---|
| T | F |
| F | T |
- Home
-
For Developers
- Programming Standards
- Developer Setup Guide
- Alternative Developer Setup Guide (linux)
- Pointers for Getting Started
- Guide to Implementing Puzzles
- Guide to Implementing the Puzzle Editor Functionality for a Puzzle
- Native Binary Compilation Information for Windows
- Test Suite Documentation
- Notes for a Future Rewrite
- For End Users