forked from youngyangyang04/leetcode-master
-
Notifications
You must be signed in to change notification settings - Fork 0
Commit
This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.
- Loading branch information
1 parent
2b86b9f
commit b808b4b
Showing
26 changed files
with
3,053 additions
and
35 deletions.
There are no files selected for viewing
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,134 @@ | ||
|
|
||
|
|
||
| > 相对于[贪心算法:跳跃游戏](https://mp.weixin.qq.com/s/606_N9j8ACKCODoCbV1lSA)难了不少,做好心里准备! | ||
| ## 45.跳跃游戏II | ||
|
|
||
| 题目地址:https://leetcode-cn.com/problems/jump-game-ii/ | ||
|
|
||
| 给定一个非负整数数组,你最初位于数组的第一个位置。 | ||
|
|
||
| 数组中的每个元素代表你在该位置可以跳跃的最大长度。 | ||
|
|
||
| 你的目标是使用最少的跳跃次数到达数组的最后一个位置。 | ||
|
|
||
| 示例: | ||
| 输入: [2,3,1,1,4] | ||
| 输出: 2 | ||
| 解释: 跳到最后一个位置的最小跳跃数是 2。从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。 | ||
|
|
||
| 说明: | ||
| 假设你总是可以到达数组的最后一个位置。 | ||
|
|
||
|
|
||
| ## 思路 | ||
|
|
||
| 本题相对于[贪心算法:跳跃游戏](https://mp.weixin.qq.com/s/606_N9j8ACKCODoCbV1lSA)还是难了不少。 | ||
|
|
||
| 但思路是相似的,还是要看最大覆盖范围。 | ||
|
|
||
| 本题要计算最小步数,那么就要想清楚什么时候步数才一定要加一呢? | ||
|
|
||
| 贪心的思路,局部最优:当前可移动距离尽可能多走,如果还没到终点,步数再加一。整体最优:一步尽可能多走,从而达到最小步数。 | ||
|
|
||
| 思路虽然是这样,但在写代码的时候还不能真的就能跳多远跳远,那样就不知道下一步最远能跳到哪里了。 | ||
|
|
||
| **所以真正解题的时候,要从覆盖范围出发,不管怎么跳,覆盖范围内一定是可以跳到的,以最小的步数增加覆盖范围,覆盖范围一旦覆盖了终点,得到的就是最小步数!** | ||
|
|
||
| **这里需要统计两个覆盖范围,当前这一步的最大覆盖和下一步最大覆盖**。 | ||
|
|
||
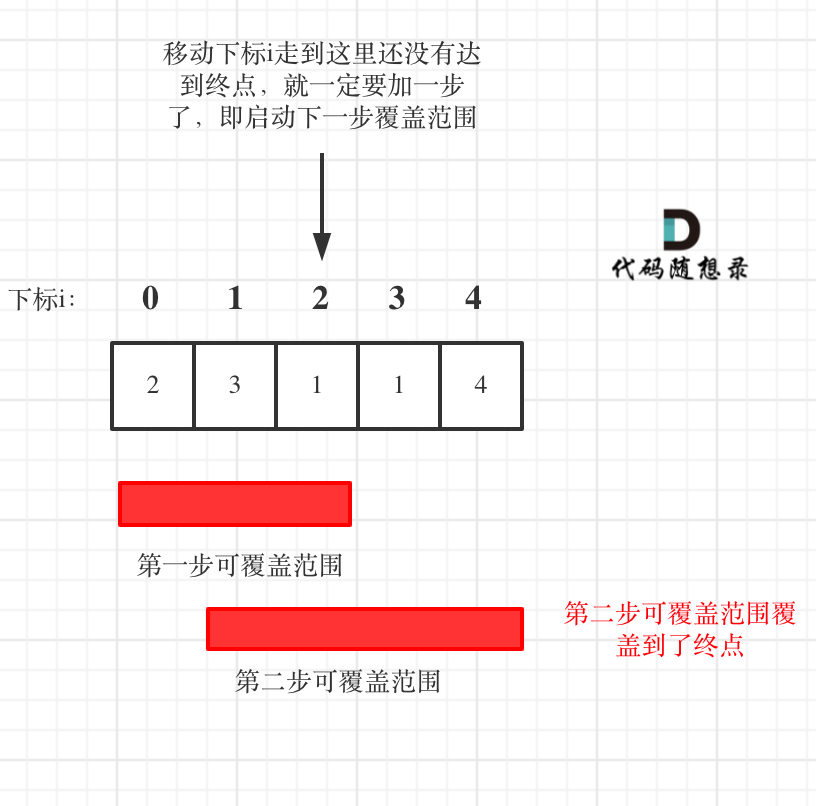
| 如果移动下标达到了当前这一步的最大覆盖最远距离了,还没有到终点的话,那么就必须再走一步来增加覆盖范围,直到覆盖范围覆盖了终点。 | ||
|
|
||
| 如图: | ||
|
|
||
|  | ||
|
|
||
| **图中覆盖范围的意义在于,只要红色的区域,最多两步一定可以到!(不用管具体怎么跳,反正一定可以跳到)** | ||
|
|
||
| ## 方法一 | ||
|
|
||
| 从图中可以看出来,就是移动下标达到了当前覆盖的最远距离下标时,步数就要加一,来增加覆盖距离。最后的步数就是最少步数。 | ||
|
|
||
| 这里还是有个特殊情况需要考虑,当移动下标达到了当前覆盖的最远距离下标时 | ||
|
|
||
| * 如果当前覆盖最远距离下标不是是集合终点,步数就加一,还需要继续走。 | ||
| * 如果当前覆盖最远距离下标就是是集合终点,步数不用加一,因为不能再往后走了。 | ||
|
|
||
| C++代码如下:(详细注释) | ||
|
|
||
| ```C++ | ||
| // 版本一 | ||
| class Solution { | ||
| public: | ||
| int jump(vector<int>& nums) { | ||
| if (nums.size() == 1) return 0; | ||
| int curDistance = 0; // 当前覆盖最远距离下标 | ||
| int ans = 0; // 记录走的最大步数 | ||
| int nextDistance = 0; // 下一步覆盖最远距离下标 | ||
| for (int i = 0; i < nums.size(); i++) { | ||
| nextDistance = max(nums[i] + i, nextDistance); // 更新下一步覆盖最远距离下标 | ||
| if (i == curDistance) { // 遇到当前覆盖最远距离下标 | ||
| if (curDistance != nums.size() - 1) { // 如果当前覆盖最远距离下标不是终点 | ||
| ans++; // 需要走下一步 | ||
| curDistance = nextDistance; // 更新当前覆盖最远距离下标(相当于加油了) | ||
| if (nextDistance >= nums.size() - 1) break; // 下一步的覆盖范围已经可以达到终点,结束循环 | ||
| } else break; // 当前覆盖最远距离下标是集合终点,不用做ans++操作了,直接结束 | ||
| } | ||
| } | ||
| return ans; | ||
| } | ||
| }; | ||
| ``` | ||
| ## 方法二 | ||
| 依然是贪心,思路和方法一差不多,代码可以简洁一些。 | ||
| **针对于方法一的特殊情况,可以统一处理**,即:移动下标只要遇到当前覆盖最远距离的下标,直接步数加一,不考虑是不是终点的情况。 | ||
| 想要达到这样的效果,只要让移动下标,最大只能移动到nums.size - 2的地方就可以了。 | ||
| 因为当移动下标指向nums.size - 2时: | ||
| * 如果移动下标等于当前覆盖最大距离下标, 需要再走一步(即ans++),因为最后一步一定是可以到的终点。(题目假设总是可以到达数组的最后一个位置),如图: | ||
| 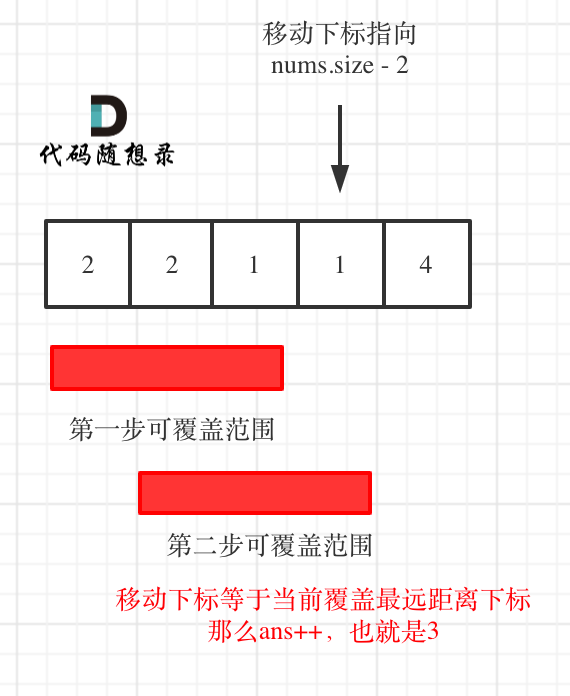 | ||
| * 如果移动下标不等于当前覆盖最大距离下标,说明当前覆盖最远距离就可以直接达到终点了,不需要再走一步。如图: | ||
| 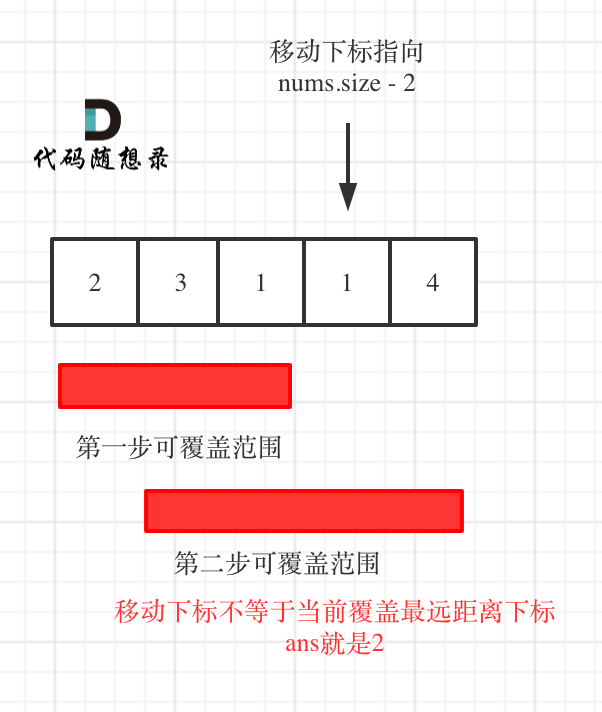 | ||
| 代码如下: | ||
| ```C++ | ||
| // 版本二 | ||
| class Solution { | ||
| public: | ||
| int jump(vector<int>& nums) { | ||
| int curDistance = 0; // 当前覆盖的最远距离下标 | ||
| int ans = 0; // 记录走的最大步数 | ||
| int nextDistance = 0; // 下一步覆盖的最远距离下标 | ||
| for (int i = 0; i < nums.size() - 1; i++) { // 注意这里是小于nums.size() - 1,这是关键所在 | ||
| nextDistance = max(nums[i] + i, nextDistance); // 更新下一步覆盖的最远距离下标 | ||
| if (i == curDistance) { // 遇到当前覆盖的最远距离下标 | ||
| curDistance = nextDistance; // 更新当前覆盖的最远距离下标 | ||
| ans++; | ||
| } | ||
| } | ||
| return ans; | ||
| } | ||
| }; | ||
| ``` | ||
|
|
||
| 可以看出版本二的代码相对于版本一简化了不少! | ||
|
|
||
| 其精髓在于控制移动下标i只移动到nums.size() - 2的位置,所以移动下标只要遇到当前覆盖最远距离的下标,直接步数加一,不用考虑别的了。 | ||
|
|
||
| ## 总结 | ||
|
|
||
| 相信大家可以发现,这道题目相当于[贪心算法:跳跃游戏](https://mp.weixin.qq.com/s/606_N9j8ACKCODoCbV1lSA)难了不止一点。 | ||
|
|
||
| 但代码又十分简单,贪心就是这么巧妙。 | ||
|
|
||
| 理解本题的关键在于:**以最小的步数增加最大的覆盖范围,直到覆盖范围覆盖了终点**,这个范围内最小步数一定可以跳到,不用管具体是怎么跳的,不纠结于一步究竟跳一个单位还是两个单位。 | ||
|
|
||
|
|
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,130 @@ | ||
|
|
||
|
|
||
| ## 53. 最大子序和 | ||
|
|
||
| 题目地址:https://leetcode-cn.com/problems/maximum-subarray/ | ||
|
|
||
| 给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。 | ||
|
|
||
| 示例: | ||
| 输入: [-2,1,-3,4,-1,2,1,-5,4] | ||
| 输出: 6 | ||
| 解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。 | ||
|
|
||
|
|
||
| ## 暴力解法 | ||
|
|
||
| 暴力解法的思路,第一层for 就是设置起始位置,第二层for循环遍历数组寻找最大值 | ||
|
|
||
| 时间复杂度:O(n^2) | ||
| 空间复杂度:O(1) | ||
| ```C++ | ||
| class Solution { | ||
| public: | ||
| int maxSubArray(vector<int>& nums) { | ||
| int result = INT32_MIN; | ||
| int count = 0; | ||
| for (int i = 0; i < nums.size(); i++) { // 设置起始位置 | ||
| count = 0; | ||
| for (int j = i; j < nums.size(); j++) { // 每次从起始位置i开始遍历寻找最大值 | ||
| count += nums[j]; | ||
| result = count > result ? count : result; | ||
| } | ||
| } | ||
| return result; | ||
| } | ||
| }; | ||
| ``` | ||
| 以上暴力的解法C++勉强可以过,其他语言就不确定了。 | ||
| ## 贪心解法 | ||
| **贪心贪的是哪里呢?** | ||
| 如果 -2 1 在一起,计算起点的时候,一定是从1开始计算,因为负数只会拉低总和,这就是贪心贪的地方! | ||
| 局部最优:当前“连续和”为负数的时候立刻放弃,从下一个元素重新计算“连续和”,因为负数加上下一个元素 “连续和”只会越来越小。 | ||
| 全局最优:选取最大“连续和” | ||
| **局部最优的情况下,并记录最大的“连续和”,可以推出全局最优**。 | ||
| 从代码角度上来讲:遍历nums,从头开始用count累积,如果count一旦加上nums[i]变为负数,那么就应该从nums[i+1]开始从0累积count了,因为已经变为负数的count,只会拖累总和。 | ||
| **这相当于是暴力解法中的不断调整最大子序和区间的起始位置**。 | ||
| **那有同学问了,区间终止位置不用调整么? 如何才能得到最大“连续和”呢?** | ||
| 区间的终止位置,其实就是如果count取到最大值了,及时记录下来了。例如如下代码: | ||
| ``` | ||
| if (count > result) result = count; | ||
| ``` | ||
| **这样相当于是用result记录最大子序和区间和(变相的算是调整了终止位置)**。 | ||
| 如动画所示: | ||
| <img src='https://tva1.sinaimg.cn/large/0081Kckwly1gmbec53gn8g30bk08ynpd.gif' width=600 alt='53.最大子序和'> </img></div> | ||
| 红色的起始位置就是贪心每次取count为正数的时候,开始一个区间的统计。 | ||
| 那么不难写出如下C++代码(关键地方已经注释) | ||
| ```C++ | ||
| class Solution { | ||
| public: | ||
| int maxSubArray(vector<int>& nums) { | ||
| int result = INT32_MIN; | ||
| int count = 0; | ||
| for (int i = 0; i < nums.size(); i++) { | ||
| count += nums[i]; | ||
| if (count > result) { // 取区间累计的最大值(相当于不断确定最大子序终止位置) | ||
| result = count; | ||
| } | ||
| if (count <= 0) count = 0; // 相当于重置最大子序起始位置,因为遇到负数一定是拉低总和 | ||
| } | ||
| return result; | ||
| } | ||
| }; | ||
| ``` | ||
| 时间复杂度:O(n) | ||
| 空间复杂度:O(1) | ||
|
|
||
| 当然题目没有说如果数组为空,应该返回什么,所以数组为空的话返回啥都可以了。 | ||
|
|
||
| ## 动态规划 | ||
|
|
||
| 当然本题还可以用动态规划来做,当前[「代码随想录」](https://img-blog.csdnimg.cn/20201124161234338.png)主要讲解贪心系列,后续到动态规划系列的时候会详细讲解本题的dp方法。 | ||
|
|
||
| 那么先给出我的dp代码如下,有时间的录友可以提前做一做: | ||
|
|
||
| ```C++ | ||
| class Solution { | ||
| public: | ||
| int maxSubArray(vector<int>& nums) { | ||
| if (nums.size() == 0) return 0; | ||
| vector<int> dp(nums.size(), 0); // dp[i]表示包括i之前的最大连续子序列和 | ||
| dp[0] = nums[0]; | ||
| int result = dp[0]; | ||
| for (int i = 1; i < nums.size(); i++) { | ||
| dp[i] = max(dp[i - 1] + nums[i], nums[i]); // 状态转移公式 | ||
| if (dp[i] > result) result = dp[i]; // result 保存dp[i]的最大值 | ||
| } | ||
| return result; | ||
| } | ||
| }; | ||
| ``` | ||
| 时间复杂度:O(n) | ||
| 空间复杂度:O(n) | ||
| ## 总结 | ||
| 本题的贪心思路其实并不好想,这也进一步验证了,别看贪心理论很直白,有时候看似是常识,但贪心的题目一点都不简单! | ||
| 后续将介绍的贪心题目都挺难的,哈哈,所以贪心很有意思,别小看贪心! | ||
Oops, something went wrong.