更新回溯算法Markdown

nowsoar · Apr 30, 2021 · 895196b · 895196b
1 parent 9a24bd3
commit 895196b
Show file tree

Hide file tree

Showing 14 changed files with 2,495 additions and 23 deletions.
diff --git a/README.md b/README.md
@@ -225,23 +225,20 @@
 7. [回溯算法：求组合总和（二）](./problems/0039.组合总和.md)
 8. [回溯算法：求组合总和（三）](./problems/0040.组合总和II.md)
 9. [回溯算法：分割回文串](./problems/0131.分割回文串.md)
-10. [回溯算法：复原IP地址](https://mp.weixin.qq.com/s/v--VmA8tp9vs4bXCqHhBuA)
-11. [回溯算法：求子集问题！](https://mp.weixin.qq.com/s/NNRzX-vJ_pjK4qxohd_LtA)
-12. [本周小结！（回溯算法系列二）](https://mp.weixin.qq.com/s/uzDpjrrMCO8DOf-Tl5oBGw)
-13. [回溯算法：求子集问题（二）](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ)
-14. [回溯算法：递增子序列](https://mp.weixin.qq.com/s/ePxOtX1ATRYJb2Jq7urzHQ)
-15. [回溯算法：排列问题！](https://mp.weixin.qq.com/s/SCOjeMX1t41wcvJq49GhMw)
-16. [回溯算法：排列问题（二）](https://mp.weixin.qq.com/s/9L8h3WqRP_h8LLWNT34YlA)
-17. [本周小结！（回溯算法系列三）](https://mp.weixin.qq.com/s/tLkt9PSo42X60w8i94ViiA)
-18. [本周小结！（回溯算法系列三）续集](https://mp.weixin.qq.com/s/kSMGHc_YpsqL2j-jb_E_Ag)
-19. [视频来了！！带你学透回溯算法（理论篇）](https://www.bilibili.com/video/BV1cy4y167mM)
-20. [视频来了！！回溯算法（力扣题目：77.组合）](https://www.bilibili.com/video/BV1ti4y1L7cv)
-21. [视频来了！！回溯算法剪枝操作（力扣题目：77.组合）](https://www.bilibili.com/video/BV1wi4y157er)
-22. [视频来了！！回溯算法（力扣题目：39.组合总和）](https://www.bilibili.com/video/BV1KT4y1M7HJ/)
-23. [回溯算法：重新安排行程](https://mp.weixin.qq.com/s/3kmbS4qDsa6bkyxR92XCTA)
-24. [回溯算法：N皇后问题](https://mp.weixin.qq.com/s/lU_QwCMj6g60nh8m98GAWg)
-25. [回溯算法：解数独](https://mp.weixin.qq.com/s/eWE9TapVwm77yW9Q81xSZQ)
-26. [一篇总结带你彻底搞透回溯算法！](https://mp.weixin.qq.com/s/r73thpBnK1tXndFDtlsdCQ)
+10. [回溯算法：复原IP地址](./problems/0093.复原IP地址.md)
+11. [回溯算法：求子集问题！](./problems/0078.子集.md)
+12. [本周小结！（回溯算法系列二）](./problems/周总结/20201107回溯周末总结.md)
+13. [回溯算法：求子集问题（二）](./problems/0090.子集II.md)
+14. [回溯算法：递增子序列](./problems/0491.递增子序列.md)
+15. [回溯算法：排列问题！](./problems/0046.全排列.md)
+16. [回溯算法：排列问题（二）](./problems/0047.全排列II.md)
+17. [本周小结！（回溯算法系列三）](./problems/周总结/20201112回溯周末总结.md)
+18. [回溯算法去重问题的另一种写法](./problems/回溯算法去重问题的另一种写法.md)
+
+23. [回溯算法：重新安排行程](./problems/0332.重新安排行程.md)
+24. [回溯算法：N皇后问题](./problems/0051.N皇后.md)
+25. [回溯算法：解数独](./problems/0037.解数独.md)
+26. [一篇总结带你彻底搞透回溯算法！](./problems/回溯总结.md)
 
 ## 贪心算法 
 

diff --git a/problems/0037.解数独.md b/problems/0037.解数独.md
@@ -0,0 +1,210 @@
+
+
+如果对回溯法理论还不清楚的同学，可以先看这个视频[视频来了！！带你学透回溯算法（理论篇）](https://mp.weixin.qq.com/s/wDd5azGIYWjbU0fdua_qBg)
+
+## 37. 解数独
+
+题目地址：https://leetcode-cn.com/problems/sudoku-solver/
+
+编写一个程序，通过填充空格来解决数独问题。
+
+一个数独的解法需遵循如下规则：
+数字 1-9 在每一行只能出现一次。
+数字 1-9 在每一列只能出现一次。
+数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。
+空白格用 '.' 表示。
+
+![解数独](https://img-blog.csdnimg.cn/202011171912586.png)
+
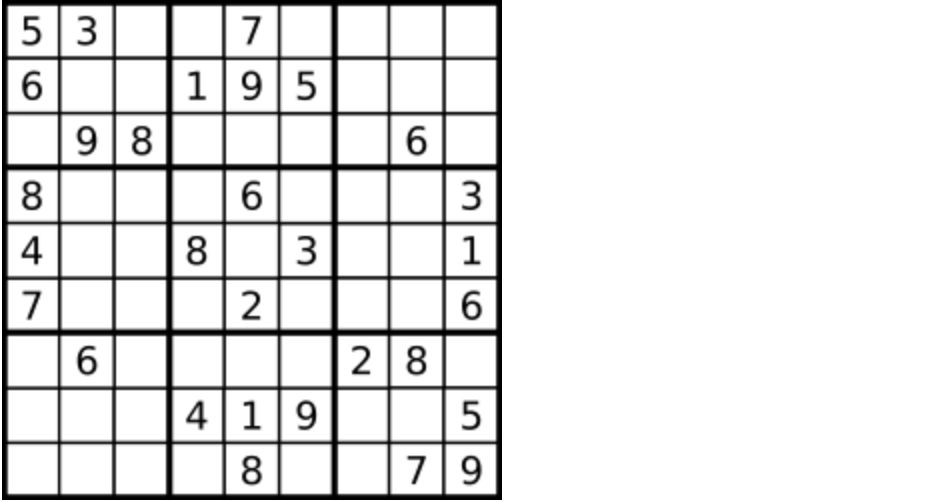+一个数独。
+
+![解数独](https://img-blog.csdnimg.cn/20201117191340669.png)
+
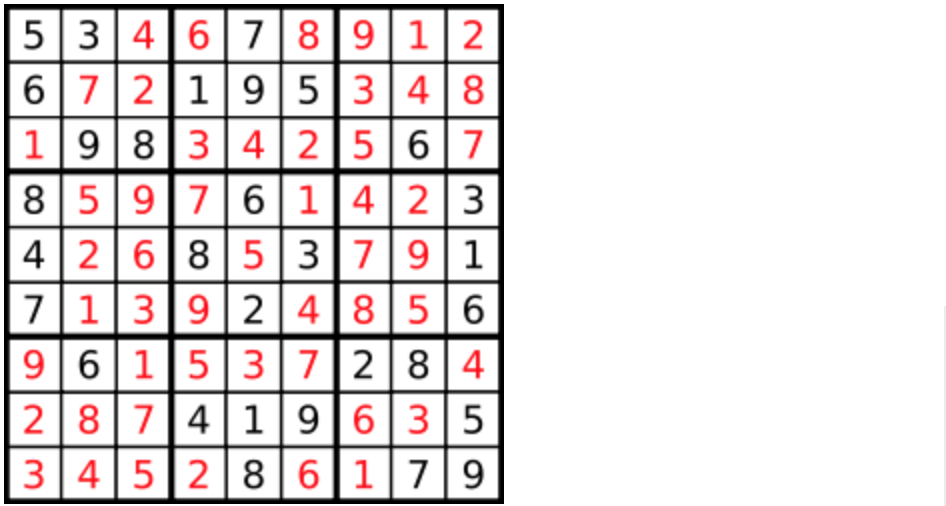+答案被标成红色。
+
+提示：
+* 给定的数独序列只包含数字 1-9 和字符 '.' 。
+* 你可以假设给定的数独只有唯一解。
+* 给定数独永远是 9x9 形式的。
+
+## 思路
+
+棋盘搜索问题可以使用回溯法暴力搜索，只不过这次我们要做的是**二维递归**。
+
+怎么做二维递归呢？
+
+大家已经跟着「代码随想录」刷过了如下回溯法题目，例如：[77.组合（组合问题）](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)，[131.分割回文串（分割问题）](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)，[78.子集（子集问题）](https://mp.weixin.qq.com/s/NNRzX-vJ_pjK4qxohd_LtA)，[46.全排列（排列问题）](https://mp.weixin.qq.com/s/SCOjeMX1t41wcvJq49GhMw)，以及[51.N皇后（N皇后问题）](https://mp.weixin.qq.com/s/lU_QwCMj6g60nh8m98GAWg)，其实这些题目都是一维递归。
+
+**如果以上这几道题目没有做过的话，不建议上来就做这道题哈！**
+
+[N皇后问题](https://mp.weixin.qq.com/s/lU_QwCMj6g60nh8m98GAWg)是因为每一行每一列只放一个皇后，只需要一层for循环遍历一行，递归来来遍历列，然后一行一列确定皇后的唯一位置。
+
+本题就不一样了，**本题中棋盘的每一个位置都要放一个数字，并检查数字是否合法，解数独的树形结构要比N皇后更宽更深**。
+
+因为这个树形结构太大了，我抽取一部分，如图所示：
+
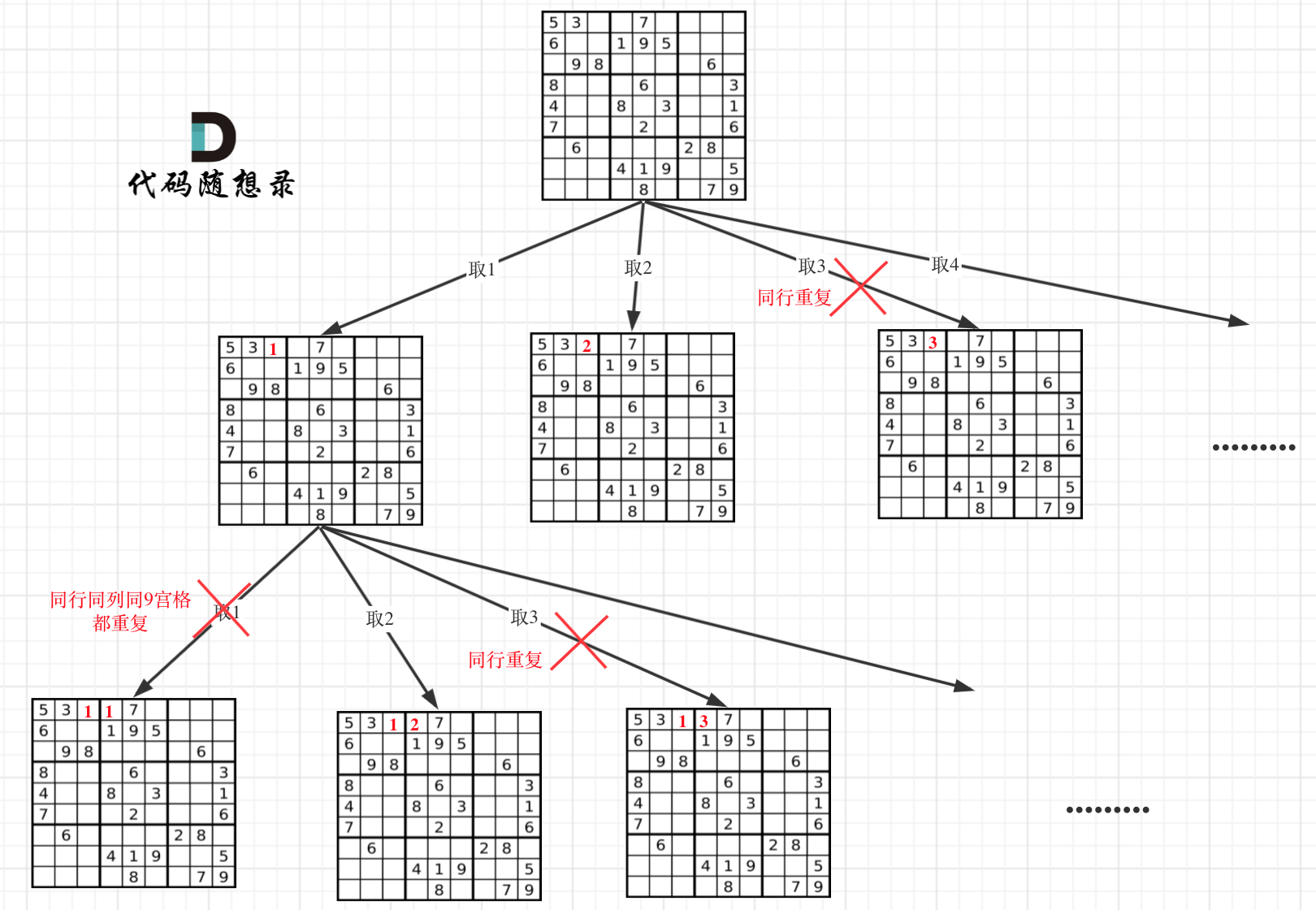+![37.解数独](https://img-blog.csdnimg.cn/2020111720451790.png)
+
+
+## 回溯三部曲
+
+* 递归函数以及参数
+
+**递归函数的返回值需要是bool类型，为什么呢？**
+
+因为解数独找到一个符合的条件（就在树的叶子节点上）立刻就返回，相当于找从根节点到叶子节点一条唯一路径，所以需要使用bool返回值，这一点在[回溯算法：N皇后问题](https://mp.weixin.qq.com/s/lU_QwCMj6g60nh8m98GAWg)中已经介绍过了，一样的道理。
+
+代码如下：
+
+```
+bool backtracking(vector<vector<char>>& board)
+```
+
+* 递归终止条件
+
+本题递归不用终止条件，解数独是要遍历整个树形结构寻找可能的叶子节点就立刻返回。
+
+**不用终止条件会不会死循环？**
+
+递归的下一层的棋盘一定比上一层的棋盘多一个数，等数填满了棋盘自然就终止（填满当然好了，说明找到结果了），所以不需要终止条件！
+
+**那么有没有永远填不满的情况呢？**
+
+这个问题我在递归单层搜索逻辑里在来讲！
+
+* 递归单层搜索逻辑
+
+![37.解数独](https://img-blog.csdnimg.cn/2020111720451790.png)
+
+在树形图中可以看出我们需要的是一个二维的递归（也就是两个for循环嵌套着递归）
+
+**一个for循环遍历棋盘的行，一个for循环遍历棋盘的列，一行一列确定下来之后，递归遍历这个位置放9个数字的可能性！**
+
+
+代码如下：（**详细看注释**）
+
+```C++
+bool backtracking(vector<vector<char>>& board) {
+    for (int i = 0; i < board.size(); i++) {        // 遍历行
+        for (int j = 0; j < board[0].size(); j++) { // 遍历列
+            if (board[i][j] != '.') continue;
+            for (char k = '1'; k <= '9'; k++) {     // (i, j) 这个位置放k是否合适
+                if (isValid(i, j, k, board)) {
+                    board[i][j] = k;                // 放置k
+                    if (backtracking(board)) return true; // 如果找到合适一组立刻返回
+                    board[i][j] = '.';              // 回溯，撤销k
+                }
+            }
+            return false;                           // 9个数都试完了，都不行，那么就返回false
+        }
+    }
+    return true; // 遍历完没有返回false，说明找到了合适棋盘位置了
+}
+```
+
+**注意这里return false的地方，这里放return false 是有讲究的**。
+
+因为如果一行一列确定下来了，这里尝试了9个数都不行，说明这个棋盘找不到解决数独问题的解！
+
+那么会直接返回， **这也就是为什么没有终止条件也不会永远填不满棋盘而无限递归下去！**
+
+## 判断棋盘是否合法
+
+判断棋盘是否合法有如下三个维度：
+
+* 同行是否重复
+* 同列是否重复
+* 9宫格里是否重复
+
+代码如下：
+
+```C++
+bool isValid(int row, int col, char val, vector<vector<char>>& board) {
+    for (int i = 0; i < 9; i++) { // 判断行里是否重复
+        if (board[row][i] == val) {
+            return false;
+        }
+    }
+    for (int j = 0; j < 9; j++) { // 判断列里是否重复
+        if (board[j][col] == val) {
+            return false;
+        }
+    }
+    int startRow = (row / 3) * 3;
+    int startCol = (col / 3) * 3;
+    for (int i = startRow; i < startRow + 3; i++) { // 判断9方格里是否重复
+        for (int j = startCol; j < startCol + 3; j++) {
+            if (board[i][j] == val ) {
+                return false;
+            }
+        }
+    }
+    return true;
+}
+```
+
+最后整体代码如下：
+
+## C++代码
+
+```C++
+class Solution {
+private:
+bool backtracking(vector<vector<char>>& board) {
+    for (int i = 0; i < board.size(); i++) {        // 遍历行
+        for (int j = 0; j < board[0].size(); j++) { // 遍历列
+            if (board[i][j] != '.') continue;
+            for (char k = '1'; k <= '9'; k++) {     // (i, j) 这个位置放k是否合适
+                if (isValid(i, j, k, board)) {
+                    board[i][j] = k;                // 放置k
+                    if (backtracking(board)) return true; // 如果找到合适一组立刻返回
+                    board[i][j] = '.';              // 回溯，撤销k
+                }
+            }
+            return false;                           // 9个数都试完了，都不行，那么就返回false
+        }
+    }
+    return true; // 遍历完没有返回false，说明找到了合适棋盘位置了
+}
+bool isValid(int row, int col, char val, vector<vector<char>>& board) {
+    for (int i = 0; i < 9; i++) { // 判断行里是否重复
+        if (board[row][i] == val) {
+            return false;
+        }
+    }
+    for (int j = 0; j < 9; j++) { // 判断列里是否重复
+        if (board[j][col] == val) {
+            return false;
+        }
+    }
+    int startRow = (row / 3) * 3;
+    int startCol = (col / 3) * 3;
+    for (int i = startRow; i < startRow + 3; i++) { // 判断9方格里是否重复
+        for (int j = startCol; j < startCol + 3; j++) {
+            if (board[i][j] == val ) {
+                return false;
+            }
+        }
+    }
+    return true;
+}
+public:
+    void solveSudoku(vector<vector<char>>& board) {
+        backtracking(board);
+    }
+};
+```
+
+## 总结
+
+解数独可以说是非常难的题目了，如果还一直停留在单层递归的逻辑中，这道题目可以让大家瞬间崩溃。
+
+所以我在开篇就提到了**二维递归**，这也是我自创词汇，希望可以帮助大家理解解数独的搜索过程。
+
+一波分析之后，在看代码会发现其实也不难，唯一难点就是理解**二维递归**的思维逻辑。
+
+**这样，解数独这么难的问题，也被我们攻克了**。
+
+**恭喜一路上坚持打卡的录友们，回溯算法已经接近尾声了，接下来就是要一波总结了**。
+
+
diff --git a/problems/0046.全排列.md b/problems/0046.全排列.md
@@ -0,0 +1,138 @@
+
+
+## 46.全排列
+
+题目链接：https://leetcode-cn.com/problems/permutations/
+
+给定一个 没有重复 数字的序列，返回其所有可能的全排列。
+
+示例:
+输入: [1,2,3]
+输出:
+[
+  [1,2,3],
+  [1,3,2],
+  [2,1,3],
+  [2,3,1],
+  [3,1,2],
+  [3,2,1]
+]
+
+## 思路
+
+此时我们已经学习了[组合问题](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)、[切割问题](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)和[子集问题](https://mp.weixin.qq.com/s/NNRzX-vJ_pjK4qxohd_LtA)，接下来看一看排列问题。
+
+相信这个排列问题就算是让你用for循环暴力把结果搜索出来，这个暴力也不是很好写。
+
+所以正如我们在[关于回溯算法，你该了解这些！](https://mp.weixin.qq.com/s/gjSgJbNbd1eAA5WkA-HeWw)所讲的为什么回溯法是暴力搜索，效率这么低，还要用它？
+
+**因为一些问题能暴力搜出来就已经很不错了！**
+
+我以[1,2,3]为例，抽象成树形结构如下：
+
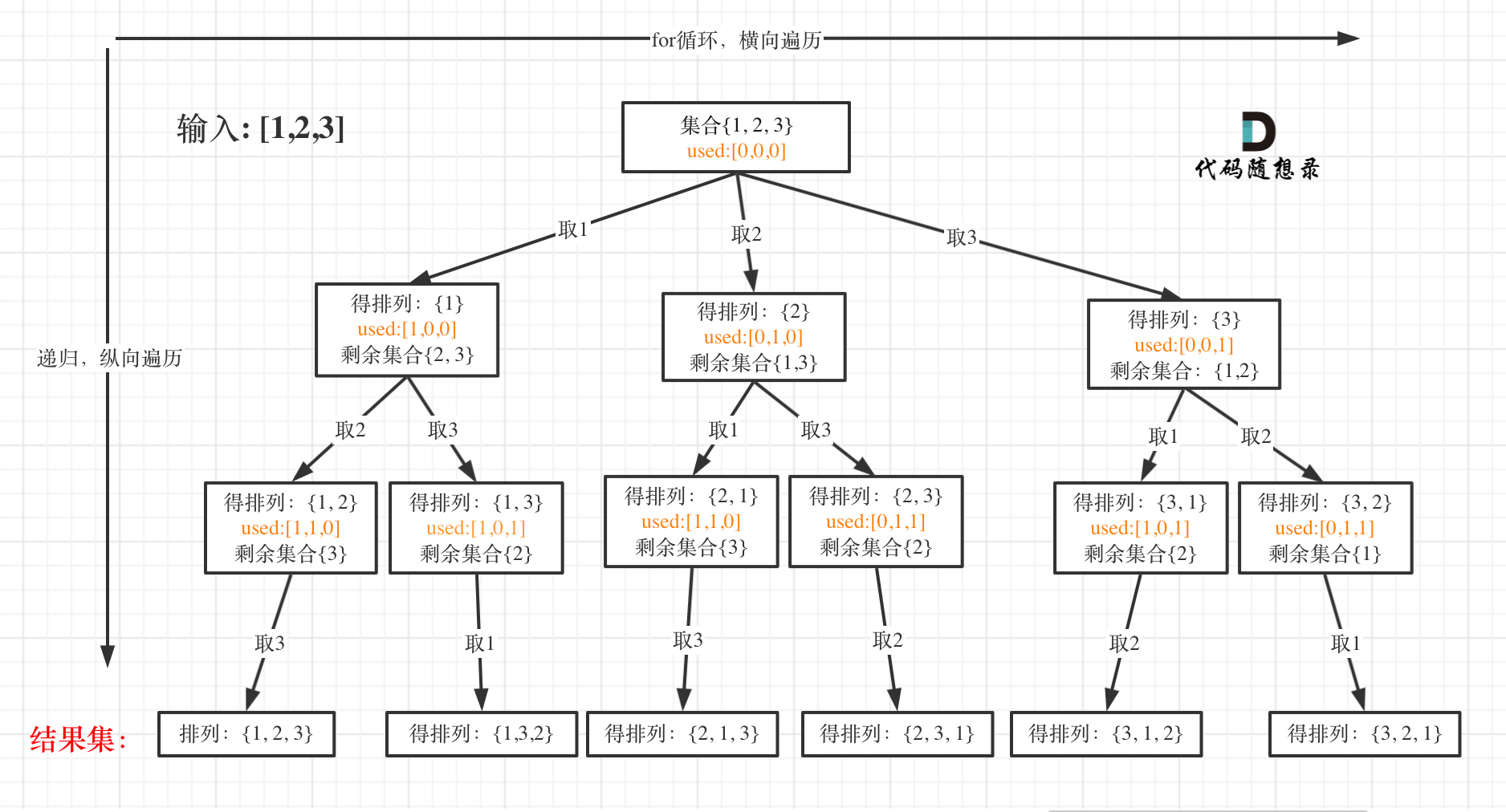+![46.全排列](https://img-blog.csdnimg.cn/20201209174225145.png)
+
+## 回溯三部曲
+
+* 递归函数参数
+
+**首先排列是有序的，也就是说[1,2] 和[2,1] 是两个集合，这和之前分析的子集以及组合所不同的地方**。
+
+可以看出元素1在[1,2]中已经使用过了，但是在[2,1]中还要在使用一次1，所以处理排列问题就不用使用startIndex了。
+
+但排列问题需要一个used数组，标记已经选择的元素，如图橘黄色部分所示:
+
+![46.全排列](https://img-blog.csdnimg.cn/20201209174225145.png)
+
+代码如下：
+
+```
+vector<vector<int>> result;
+vector<int> path;
+void backtracking (vector<int>& nums, vector<bool>& used)
+```
+
+* 递归终止条件
+
+![46.全排列](https://img-blog.csdnimg.cn/20201209174225145.png)
+
+可以看出叶子节点，就是收割结果的地方。
+
+那么什么时候，算是到达叶子节点呢？
+
+当收集元素的数组path的大小达到和nums数组一样大的时候，说明找到了一个全排列，也表示到达了叶子节点。
+
+代码如下：
+
+```
+// 此时说明找到了一组
+if (path.size() == nums.size()) {
+    result.push_back(path);
+    return;
+}
+```
+
+* 单层搜索的逻辑
+
+这里和[组合问题](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)、[切割问题](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)和[子集问题](https://mp.weixin.qq.com/s/NNRzX-vJ_pjK4qxohd_LtA)最大的不同就是for循环里不用startIndex了。
+
+因为排列问题，每次都要从头开始搜索，例如元素1在[1,2]中已经使用过了，但是在[2,1]中还要再使用一次1。
+
+**而used数组，其实就是记录此时path里都有哪些元素使用了，一个排列里一个元素只能使用一次**。
+
+代码如下：
+
+```
+for (int i = 0; i < nums.size(); i++) {
+    if (used[i] == true) continue; // path里已经收录的元素，直接跳过
+    used[i] = true;
+    path.push_back(nums[i]);
+    backtracking(nums, used);
+    path.pop_back();
+    used[i] = false;
+}
+```
+
+整体C++代码如下：
+
+
+```C++
+class Solution {
+public:
+    vector<vector<int>> result;
+    vector<int> path;
+    void backtracking (vector<int>& nums, vector<bool>& used) {
+        // 此时说明找到了一组
+        if (path.size() == nums.size()) {
+            result.push_back(path);
+            return;
+        }
+        for (int i = 0; i < nums.size(); i++) {
+            if (used[i] == true) continue; // path里已经收录的元素，直接跳过
+            used[i] = true;
+            path.push_back(nums[i]);
+            backtracking(nums, used);
+            path.pop_back();
+            used[i] = false;
+        }
+    }
+    vector<vector<int>> permute(vector<int>& nums) {
+        result.clear();
+        path.clear();
+        vector<bool> used(nums.size(), false);
+        backtracking(nums, used);
+        return result;
+    }
+};
+```
+
+## 总结
+
+大家此时可以感受出排列问题的不同：
+
+* 每层都是从0开始搜索而不是startIndex
+* 需要used数组记录path里都放了哪些元素了
+
+排列问题是回溯算法解决的经典题目，大家可以好好体会体会。
+
+