更新动态规划专题Markdown文件

README.md

@@ -154,9 +154,10 @@
 4. [字符串：花式反转还不够！](./problems/0151.翻转字符串里的单词.md)
 5. [链表：听说过两天反转链表又写不出来了？](./problems/0206.翻转链表.md)
 6. [链表：环找到了，那入口呢？](./problems/0142.环形链表II.md)
-7. [哈希表：解决了两数之和，那么能解决三数之和么？](./problems/0015.三数之和.md)
-8. [双指针法：一样的道理，能解决四数之和](./problems/0018.四数之和.md)
-9. [双指针法：总结篇！](./problems/双指针总结.md)
+7. [链表：删除链表的倒数第 N 个结点](./problems/0019.删除链表的倒数第N个节点.md)
+8. [哈希表：解决了两数之和，那么能解决三数之和么？](./problems/0015.三数之和.md)
+9. [双指针法：一样的道理，能解决四数之和](./problems/0018.四数之和.md)
+10. [双指针法：总结篇！](./problems/双指针总结.md)
 
 ## 栈与队列
 
@@ -276,77 +277,75 @@
 
 动态规划专题已经开始啦，来不及解释了，小伙伴们上车别掉队！
 
-1. [关于动态规划，你该了解这些！](https://mp.weixin.qq.com/s/ocZwfPlCWrJtVGACqFNAag)
-2. [动态规划：斐波那契数](https://mp.weixin.qq.com/s/ko0zLJplF7n_4TysnPOa_w)
-3. [动态规划：爬楼梯](https://mp.weixin.qq.com/s/Ohop0jApSII9xxOMiFhGIw)
-4. [动态规划：使用最小花费爬楼梯](https://mp.weixin.qq.com/s/djZB9gkyLFAKcQcSvKDorA)
-5. [本周小结！（动态规划系列一）](https://mp.weixin.qq.com/s/95VqGEDhtBBBSb-rM4QSMA)
-6. [动态规划：不同路径](https://mp.weixin.qq.com/s/MGgGIt4QCpFMROE9X9he_A)
-7. [动态规划：不同路径还不够，要有障碍！](https://mp.weixin.qq.com/s/lhqF0O4le9-wvalptOVOww)
-8. [动态规划：整数拆分，你要怎么拆？](https://mp.weixin.qq.com/s/cVbyHrsWH_Rfzlj-ESr01A)
-9. [动态规划：不同的二叉搜索树](https://mp.weixin.qq.com/s/8VE8pDrGxTf8NEVYBDwONw)
-10. [本周小结！（动态规划系列二）](https://mp.weixin.qq.com/s/VVsDwTP57g1f9aVsg6wShw)
+1. [关于动态规划，你该了解这些！](./problems/动态规划理论基础.md)
+2. [动态规划：斐波那契数](./problems/0509.斐波那契数.md)
+3. [动态规划：爬楼梯](./problems/0070.爬楼梯.md)
+4. [动态规划：使用最小花费爬楼梯](./problems/0746.使用最小花费爬楼梯.md)
+5. [本周小结！（动态规划系列一）](./problems/周总结/20210107动规周末总结.md)
+6. [动态规划：不同路径](./problems/0062.不同路径.md)
+7. [动态规划：不同路径还不够，要有障碍！](./problems/0063.不同路径II.md)
+8. [动态规划：整数拆分，你要怎么拆？](./problems/0343.整数拆分.md)
+9. [动态规划：不同的二叉搜索树](./problems/0096.不同的二叉搜索树.md)
+10. [本周小结！（动态规划系列二）](./problems/周总结/20210114动规周末总结.md)
 
 背包问题系列：
 
 <img src='https://img-blog.csdnimg.cn/202102261550480.png' width=500 alt='背包问题大纲'> </img></div>
 
-11. [动态规划：关于01背包问题，你该了解这些！](https://mp.weixin.qq.com/s/FwIiPPmR18_AJO5eiidT6w)
-12. [动态规划：关于01背包问题，你该了解这些！（滚动数组）](https://mp.weixin.qq.com/s/M4uHxNVKRKm5HPjkNZBnFA)
-13. [动态规划：分割等和子集可以用01背包！](https://mp.weixin.qq.com/s/sYw3QtPPQ5HMZCJcT4EaLQ)
-14. [动态规划：最后一块石头的重量 II](https://mp.weixin.qq.com/s/WbwAo3jaUaNJjvhHgq0BGg)
-15. [本周小结！（动态规划系列三）](https://mp.weixin.qq.com/s/7emRqR1O3scH63jbaE678A)
-16. [动态规划：目标和！](https://mp.weixin.qq.com/s/2pWmaohX75gwxvBENS-NCw)
-17. [动态规划：一和零！](https://mp.weixin.qq.com/s/x-u3Dsp76DlYqtCe0xEKJw) 
-18. [动态规划：关于完全背包，你该了解这些！](https://mp.weixin.qq.com/s/akwyxlJ4TLvKcw26KB9uJw)
-19. [动态规划：给你一些零钱，你要怎么凑？](https://mp.weixin.qq.com/s/PlowDsI4WMBOzf3q80AksQ)
-20. [本周小结！（动态规划系列四）](https://mp.weixin.qq.com/s/vfEXwcOlrSBBcv9gg8VDJQ)
-21. [动态规划：Carl称它为排列总和！](https://mp.weixin.qq.com/s/Iixw0nahJWQgbqVNk8k6gA)
-22. [动态规划：以前我没得选，现在我选择再爬一次！](https://mp.weixin.qq.com/s/e_wacnELo-2PG76EjrUakA)
-23. [动态规划： 给我个机会，我再兑换一次零钱](https://mp.weixin.qq.com/s/dyk-xNilHzNtVdPPLObSeQ)
-24. [动态规划：一样的套路，再求一次完全平方数](https://mp.weixin.qq.com/s/VfJT78p7UGpDZsapKF_QJQ)
-25. [本周小结！（动态规划系列五）](https://mp.weixin.qq.com/s/znj-9j8mWymRFaPjJN2Qnw)
-26. [动态规划：单词拆分](https://mp.weixin.qq.com/s/3Spx1B6MbIYjS8YkVbByzA)
-27. [动态规划：关于多重背包，你该了解这些！](https://mp.weixin.qq.com/s/b-UUUmbvG7URWyCjQkiuuQ)
-28. [听说背包问题很难？ 这篇总结篇来拯救你了](https://mp.weixin.qq.com/s/ZOehl3U1mDiyOQjFG1wNJA)
+11. [动态规划：关于01背包问题，你该了解这些！](./problems/背包理论基础01背包-1.md)
+12. [动态规划：关于01背包问题，你该了解这些！（滚动数组）](./problems/背包理论基础01背包-2.md)
+13. [动态规划：分割等和子集可以用01背包！](./problems/0416.分割等和子集.md)
+14. [动态规划：最后一块石头的重量 II](./problems/1049.最后一块石头的重量II.md)
+15. [本周小结！（动态规划系列三）](./problems/周总结/20210121动规周末总结.md)
+16. [动态规划：目标和！](./problems/0494.目标和.md)
+17. [动态规划：一和零！](./problems/0474.一和零.md) 
+18. [动态规划：关于完全背包，你该了解这些！](./problems/背包问题理论基础完全背包.md)
+19. [动态规划：给你一些零钱，你要怎么凑？](./problems/0518.零钱兑换II.md)
+20. [本周小结！（动态规划系列四）](./problems/周总结/20210128动规周末总结.md)
+21. [动态规划：Carl称它为排列总和！](./problems/0377.组合总和Ⅳ.md)
+22. [动态规划：以前我没得选，现在我选择再爬一次！](./problems/0070.爬楼梯完全背包版本.md)
+23. [动态规划： 给我个机会，我再兑换一次零钱](./problems/0322.零钱兑换.md)
+24. [动态规划：一样的套路，再求一次完全平方数](./problems/0279.完全平方数.md)
+25. [本周小结！（动态规划系列五）](./problems/周总结/20210204动规周末总结.md)
+26. [动态规划：单词拆分](./problems/0139.单词拆分.md)
+27. [动态规划：关于多重背包，你该了解这些！](./problems/背包问题理论基础多重背包.md)
+28. [听说背包问题很难？ 这篇总结篇来拯救你了](./problems/背包总结篇.md)
 
 打家劫舍系列：
 
-29. [动态规划：开始打家劫舍！](https://mp.weixin.qq.com/s/UZ31WdLEEFmBegdgLkJ8Dw)
-30. [动态规划：继续打家劫舍！](https://mp.weixin.qq.com/s/kKPx4HpH3RArbRcxAVHbeQ)
-31. [动态规划：还要打家劫舍！](https://mp.weixin.qq.com/s/BOJ1lHsxbQxUZffXlgglEQ)
+29. [动态规划：开始打家劫舍！](./problems/0198.打家劫舍.md)
+30. [动态规划：继续打家劫舍！](./problems/0213.打家劫舍II.md)
+31. [动态规划：还要打家劫舍！](./problems/0337.打家劫舍III.md)
 
 股票系列：
 
 <img src='https://code-thinking.cdn.bcebos.com/pics/%E8%82%A1%E7%A5%A8%E9%97%AE%E9%A2%98%E6%80%BB%E7%BB%93.jpg' width=500 alt='股票问题总结'> </img></div>
 
-32. [动态规划：买卖股票的最佳时机](https://mp.weixin.qq.com/s/keWo5qYJY4zmHn3amfXdfQ)
-33. [动态规划：本周我们都讲了这些（系列六）](https://mp.weixin.qq.com/s/GVu-6eF0iNkpVDKRXTPOTA)
-33. [动态规划：买卖股票的最佳时机II](https://mp.weixin.qq.com/s/d4TRWFuhaY83HPa6t5ZL-w)
-34. [动态规划：买卖股票的最佳时机III](https://mp.weixin.qq.com/s/Sbs157mlVDtAR0gbLpdKzg)
-35. [动态规划：买卖股票的最佳时机IV](https://mp.weixin.qq.com/s/jtxZJWAo2y5sUsW647Z5cw)
-36. [动态规划：最佳买卖股票时机含冷冻期](https://mp.weixin.qq.com/s/TczJGFAPnkjH9ET8kwH1OA)
-37. [动态规划：本周我们都讲了这些（系列七）](https://mp.weixin.qq.com/s/vdzDlrEvhXWRzblTnOnzKg)
-38. [动态规划：买卖股票的最佳时机含手续费](https://mp.weixin.qq.com/s/2Cd_uINjerZ25VHH0K2IBQ)
-39. [动态规划：股票系列总结篇](https://mp.weixin.qq.com/s/sC5XyEtDQWkonKnbCvZhDw)
+32. [动态规划：买卖股票的最佳时机](./problems/0121.买卖股票的最佳时机.md)
+33. [动态规划：本周我们都讲了这些（系列六）](./problems/周总结/20210225动规周末总结.md)
+33. [动态规划：买卖股票的最佳时机II](./problems/0122.买卖股票的最佳时机II（动态规划）.md)
+34. [动态规划：买卖股票的最佳时机III](./problems/0123.买卖股票的最佳时机III.md)
+35. [动态规划：买卖股票的最佳时机IV](./problems/0188.买卖股票的最佳时机IV.md)
+36. [动态规划：最佳买卖股票时机含冷冻期](./problems/0309.最佳买卖股票时机含冷冻期.md)
+37. [动态规划：本周我们都讲了这些（系列七）](./problems/周总结/20210304动规周末总结.md)
+38. [动态规划：买卖股票的最佳时机含手续费](./problems/0714.买卖股票的最佳时机含手续费（动态规划）.md)
+39. [动态规划：股票系列总结篇](./problems/动态规划-股票问题总结篇.md)
 
 子序列系列： 
 
-40. [动态规划：最长递增子序列](https://mp.weixin.qq.com/s/f8nLO3JGfgriXep_gJQpqQ)
-41. [动态规划：最长连续递增序列](https://mp.weixin.qq.com/s/c0Nn0TtjkTISVdqRsyMmyA)
-42. [动态规划：最长重复子数组](https://mp.weixin.qq.com/s/U5WaWqBwdoxzQDotOdWqZg)
-43. [动态规划：最长公共子序列](https://mp.weixin.qq.com/s/Qq0q4HaE4TyasCTj2WGFOg)
-44. [动态规划：本周我们都讲了这些（系列八）](https://mp.weixin.qq.com/s/KJNNOzGxTYhr1ks7tHvk0g)
-45. [动态规划：不相交的线](https://mp.weixin.qq.com/s/krfYzSYEO8jIoVfyHzR0rw)
-46. [动态规划：最大子序和](https://mp.weixin.qq.com/s/2Xtyi2L4r8sM-BcxgUKmcA)
-47. [动态规划：判断子序列](https://mp.weixin.qq.com/s/2pjT4B4fjfOx5iB6N6xyng)
-48. [动态规划：不同的子序列](https://mp.weixin.qq.com/s/1SULY2XVSROtk_hsoVLu8A)
-49. [动态规划：两个字符串的删除操作](https://mp.weixin.qq.com/s/a8BerpqSf76DCqkPDJrpYg)
-50. [动态规划：本周我们都讲了这些（系列十）](https://mp.weixin.qq.com/s/ES1SXf54047496YnNdeirA)
-51. [动态规划：编辑距离](https://mp.weixin.qq.com/s/8aG71XjSgZG6kZbiAdkJnQ)
-52. [为了绝杀编辑距离，我做了三步铺垫，你都知道么？](https://mp.weixin.qq.com/s/kbs4kCUzg8gPFttF9H3Yyw)
-53. [动态规划：回文子串](https://mp.weixin.qq.com/s/2WetyP6IYQ6VotegepVpEw)
-54. [动态规划：最长回文子序列](https://mp.weixin.qq.com/s/jbd3p4QPm5Kh1s2smTzWag)
+40. [动态规划：最长递增子序列](./problems/0300.最长上升子序列.md)
+41. [动态规划：最长连续递增序列](./problems/0674.最长连续递增序列.md)
+42. [动态规划：最长重复子数组](./problems/0718.最长重复子数组.md)
+43. [动态规划：最长公共子序列](./problems/1143.最长公共子序列.md)
+45. [动态规划：不相交的线](./problems/1035.不相交的线.md)
+46. [动态规划：最大子序和](./problems/0053.最大子序和（动态规划）.md)
+47. [动态规划：判断子序列](./problems/0392.判断子序列.md)
+48. [动态规划：不同的子序列](./problems/0115.不同的子序列.md)
+49. [动态规划：两个字符串的删除操作](./problems/0583.两个字符串的删除操作.md)
+51. [动态规划：编辑距离](./problems/0072.编辑距离.md)
+52. [为了绝杀编辑距离，Carl做了三步铺垫，你都知道么？](./problems/为了绝杀编辑距离，卡尔做了三步铺垫.md)
+53. [动态规划：回文子串](./problems/0647.回文子串.md)
+54. [动态规划：最长回文子序列](./problems/0516.最长回文子序列.md)
 
 
 （持续更新中....）
@@ -371,11 +370,12 @@
 
 [各类基础算法模板](https://github.com/youngyangyang04/leetcode/blob/master/problems/算法模板.md)
 
-# 知识星球精选
+# 备战秋招
 
 1. [技术比较弱，也对技术不感兴趣，如何选择方向？](https://mp.weixin.qq.com/s/ZCzFiAHZHLqHPLJQXNm75g)
 2. [刷题就用库函数了，怎么了？](https://mp.weixin.qq.com/s/6K3_OSaudnHGq2Ey8vqYfg)
 3. [关于实习，大家可能有点迷茫！](https://mp.weixin.qq.com/s/xcxzi7c78kQGjvZ8hh7taA)
+4. [马上秋招了，慌得很！](https://mp.weixin.qq.com/s/7q7W8Cb2-a5U5atZdOnOFA)
 
 # B站算法视频讲解 
 

problems/0019.删除链表的倒数第N个节点.md

@@ -7,8 +7,31 @@
 
 
 
+
 ## 19.删除链表的倒数第N个节点
 
+题目链接：https://leetcode-cn.com/problems/remove-nth-node-from-end-of-list/
+
+给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。
+
+进阶：你能尝试使用一趟扫描实现吗？
+
+示例 1：
+
+![19.删除链表的倒数第N个节点](https://img-blog.csdnimg.cn/20210510085957392.png)
+
+输入：head = [1,2,3,4,5], n = 2
+输出：[1,2,3,5]
+示例 2：
+
+输入：head = [1], n = 1
+输出：[]
+示例 3：
+
+输入：head = [1,2], n = 1
+输出：[1]
+
+
 ## 思路
 
 双指针的经典应用，如果要删除倒数第n个节点，让fast移动n步，然后让fast和slow同时移动，直到fast指向链表末尾。删掉slow所指向的节点就可以了。
@@ -17,8 +40,7 @@
 
 分为如下几步：
 
-* 首先这里我推荐大家使用虚拟头结点，这样方面处理删除实际头结点的逻辑，如果虚拟头结点不清楚，可以看这篇： [链表：听说用虚拟头节点会方便很多？](https://mp.weixin.qq.com/s/slM1CH5Ew9XzK93YOQYSjA)
-
+* 首先这里我推荐大家使用虚拟头结点，这样方面处理删除实际头结点的逻辑，如果虚拟头结点不清楚，可以看这篇： [链表：听说用虚拟头节点会方便很多？](https://mp.weixin.qq.com/s/L5aanfALdLEwVWGvyXPDqA)
 
 * 定义fast指针和slow指针，初始值为虚拟头结点，如图：
 
@@ -58,7 +80,7 @@ public:
 ```
 
 
-## 其他语言补充
+## 其他语言版本
 
 java:
 

problems/0053.最大子序和.md

@@ -74,7 +74,7 @@ if (count > result) result = count;
 
 如动画所示：
 
-<img src='https://tva1.sinaimg.cn/large/0081Kckwly1gmbec53gn8g30bk08ynpd.gif' width=600 alt='53.最大子序和'> </img></div>
+![53.最大子序和](https://code-thinking.cdn.bcebos.com/gifs/53.%E6%9C%80%E5%A4%A7%E5%AD%90%E5%BA%8F%E5%92%8C.gif)
 
 红色的起始位置就是贪心每次取count为正数的时候，开始一个区间的统计。
 

problems/0053.最大子序和（动态规划）.md

@@ -0,0 +1,86 @@
+
+## 53. 最大子序和
+
+题目地址：https://leetcode-cn.com/problems/maximum-subarray/
+
+给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。
+
+示例:
+输入: [-2,1,-3,4,-1,2,1,-5,4]
+输出: 6
+解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。
+
+## 思路
+
+这道题之前我们在讲解贪心专题的时候用贪心算法解决过一次，[贪心算法：最大子序和](https://mp.weixin.qq.com/s/DrjIQy6ouKbpletQr0g1Fg)。
+
+这次我们用动态规划的思路再来分析一次。
+
+动规五部曲如下：
+
+1. 确定dp数组（dp table）以及下标的含义
+
+**dp[i]：包括下标i之前的最大连续子序列和为dp[i]**。
+
+2. 确定递推公式
+
+dp[i]只有两个方向可以推出来：
+
+* dp[i - 1] + nums[i]，即：nums[i]加入当前连续子序列和
+* nums[i]，即：从头开始计算当前连续子序列和
+
+一定是取最大的，所以dp[i] = max(dp[i - 1] + nums[i], nums[i]);
+
+3. dp数组如何初始化
+
+从递推公式可以看出来dp[i]是依赖于dp[i - 1]的状态，dp[0]就是递推公式的基础。
+
+dp[0]应该是多少呢?
+
+更具dp[i]的定义，很明显dp[0]因为为nums[0]即dp[0] = nums[0]。
+
+4. 确定遍历顺序
+
+递推公式中dp[i]依赖于dp[i - 1]的状态，需要从前向后遍历。
+
+5. 举例推导dp数组
+
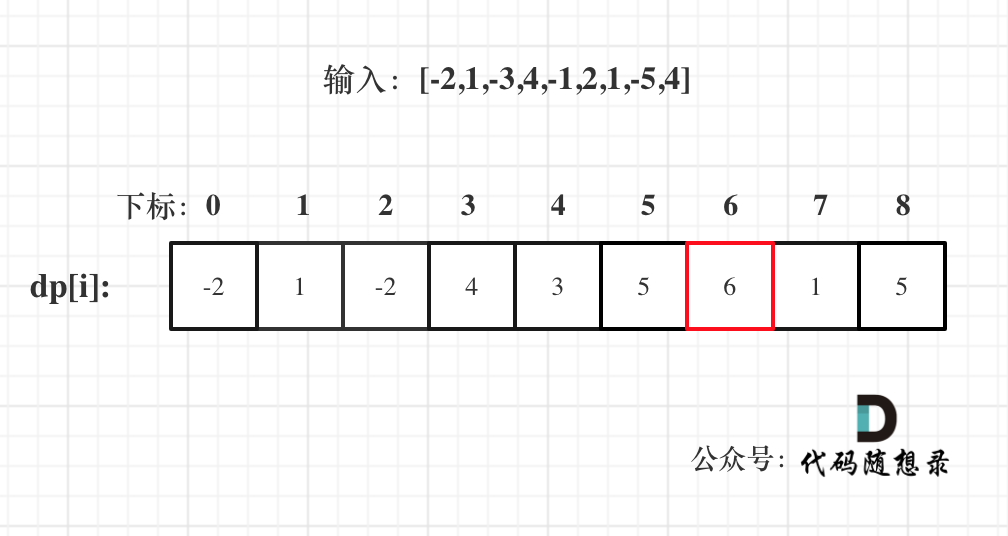
+以示例一为例，输入：nums = [-2,1,-3,4,-1,2,1,-5,4]，对应的dp状态如下：
+![53.最大子序和（动态规划）](https://img-blog.csdnimg.cn/20210303104129101.png)
+
+**注意最后的结果可不是dp[nums.size() - 1]！** ，而是dp[6]。
+
+在回顾一下dp[i]的定义：包括下标i之前的最大连续子序列和为dp[i]。
+
+那么我们要找最大的连续子序列，就应该找每一个i为终点的连续最大子序列。
+
+所以在递推公式的时候，可以直接选出最大的dp[i]。
+
+以上动规五部曲分析完毕，完整代码如下：
+
+```C++
+class Solution {
+public:
+    int maxSubArray(vector<int>& nums) {
+        if (nums.size() == 0) return 0;
+        vector<int> dp(nums.size());
+        dp[0] = nums[0];
+        int result = dp[0];
+        for (int i = 1; i < nums.size(); i++) {
+            dp[i] = max(dp[i - 1] + nums[i], nums[i]); // 状态转移公式
+            if (dp[i] > result) result = dp[i]; // result 保存dp[i]的最大值
+        }
+        return result;
+    }
+};
+```
+* 时间复杂度：O(n)
+* 空间复杂度：O(n)
+
+
+## 总结
+
+这道题目用贪心也很巧妙，但有一点绕，需要仔细想一想，如果想回顾一下贪心就看这里吧：[贪心算法：最大子序和](https://mp.weixin.qq.com/s/DrjIQy6ouKbpletQr0g1Fg)
+
+动规的解法还是很直接的。
+