-
Notifications
You must be signed in to change notification settings - Fork 2
MeshMaps
Navigation is the task of going from A to B. Or, in other words, changing the state of A as long as it reaches B. It historically includes:
- Knowing the state of A: Localization
- Planning a path to B: Path Planning / Global Planning
- Planning and executing commands along the path, i.e. changing A: Controlling / Local Planning
Maps are used to achieve this. Your vacuum cleaner is probably using a 2D occupancy grid for localization and for planning paths to B. It is also possible to use those grids for 3D navigation, by applying steepness information to them. However, there will always be a situation which is not representable, since it is simply not possible to represent a 3D environment by a 2D map. I promise you that I will find a situation where any "enriched" 2D map will break.
Therefore, we tried to find a 3D representation for a map that is computationally efficient for all the operations we need, has a low memory footprint, and is capable of representing even challenging environments. For this guide, we reduce the choice to three potential data structures: point clouds, voxel-based maps, triangle meshes.
In the following guide, we create simple but realistic examples to show how mapping is done using those three representations. We start by creating the following world which resembles a cross-section of a hill next to a valley.
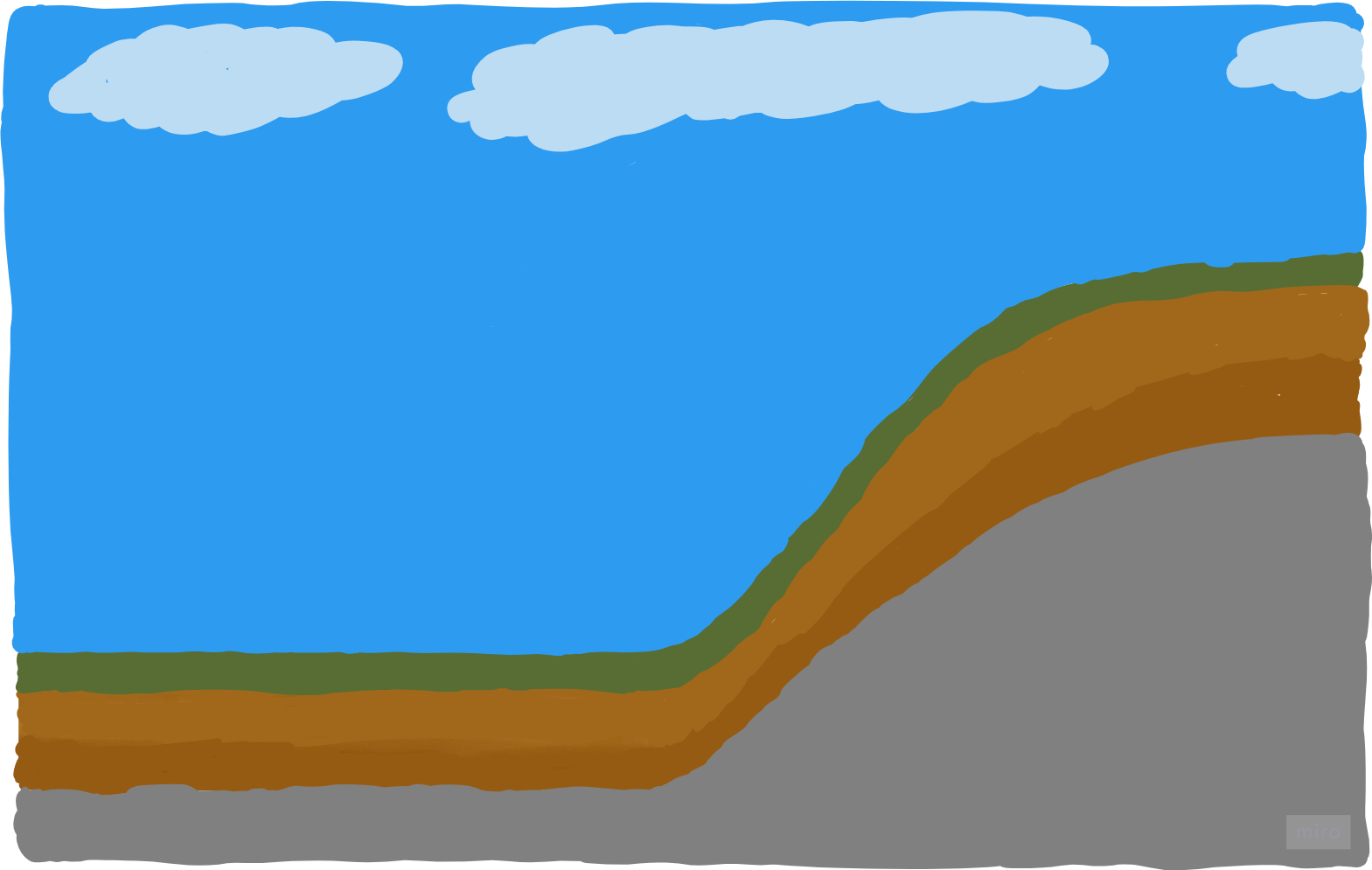
We call this world "Alps-world". Now we make a little mind game for finding a memory-friendly data structure: Represent the surface by 7 primitives. A primitive of a
- point cloud is simply a point.
- voxel-based map is a voxel or in 2D a square.
- triangle mesh is a triangle or in 2D a line.
Representing the Alps-world's surface by a point cloud using 7 primitives, i.e. points, could result in the following map:
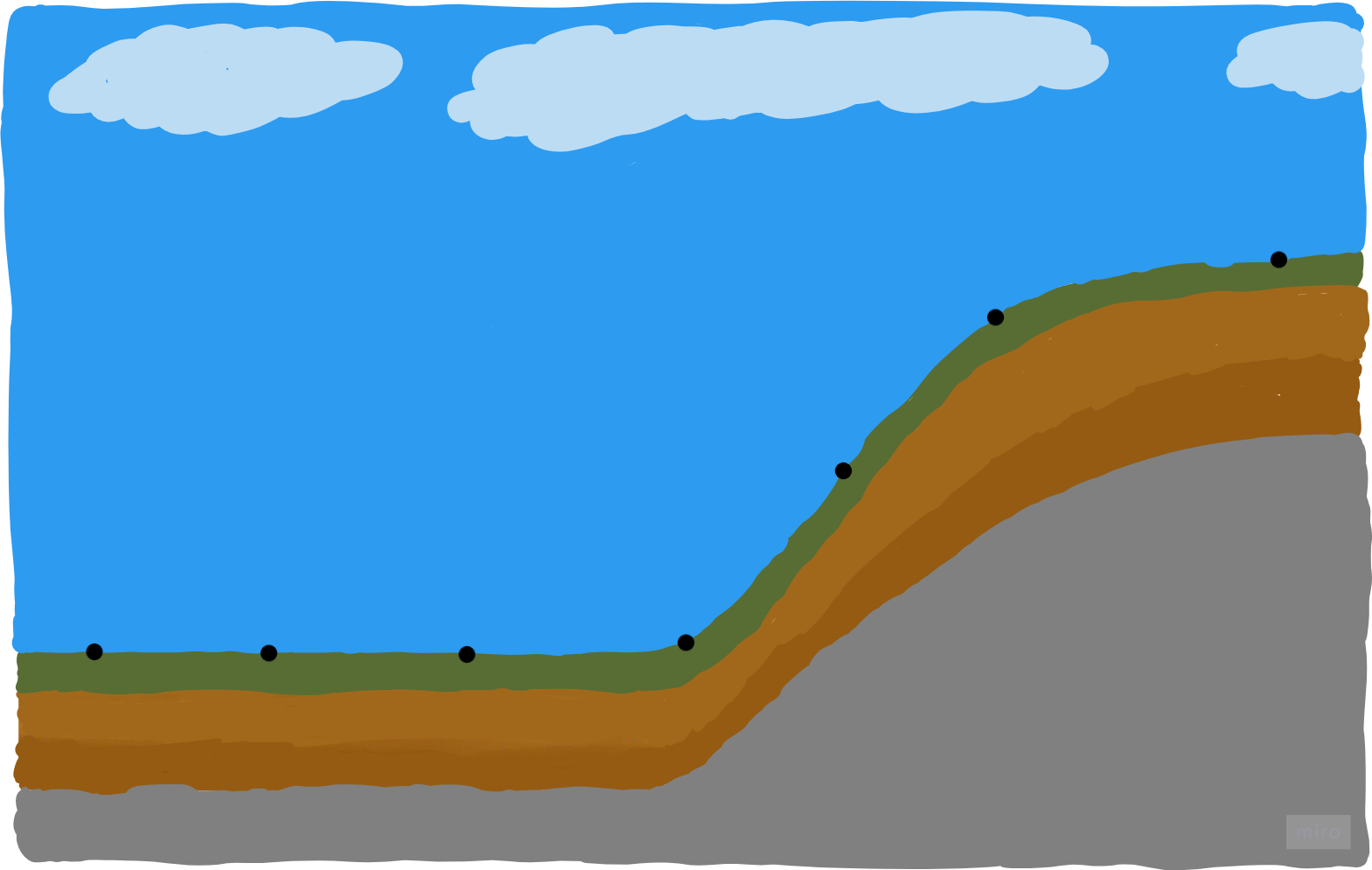
This representation is the most raw form of building a map from range sensor data, e.g. LiDAR, as every point can be an unchanged range measurement. It doesn't contain any interpolation error in between those points, since we are not interpolating inside the map itself.
However, for navigation, the problem is that we don't know what is between those points. For example there can be another world represented by the same point cloud map:
| Alps 1 | Alps 2 |
|---|---|
 |
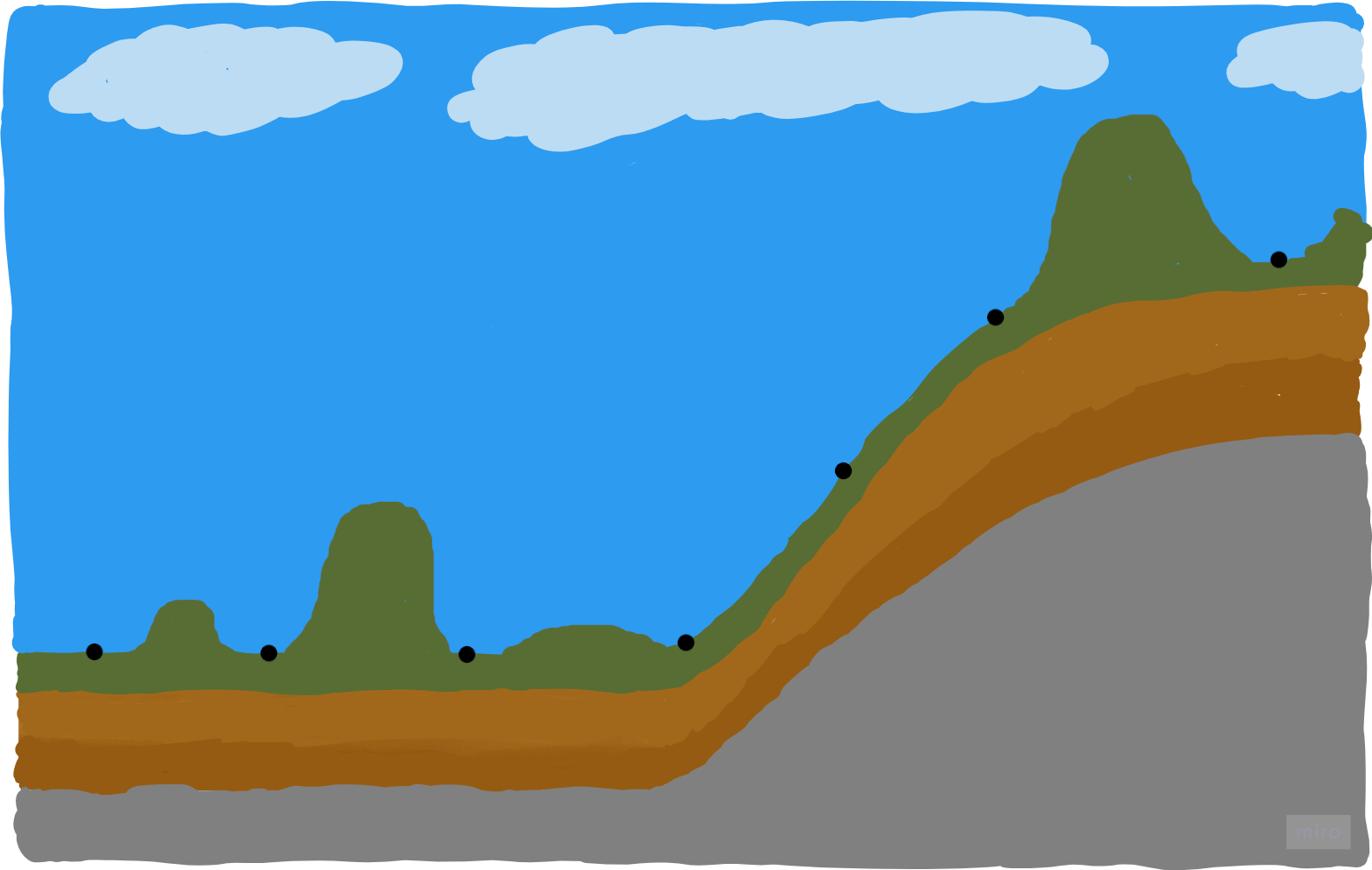 |
Representing the Alps world's surface by a voxel-based map using 7 primitives, i.e. squares, could result in the following map:
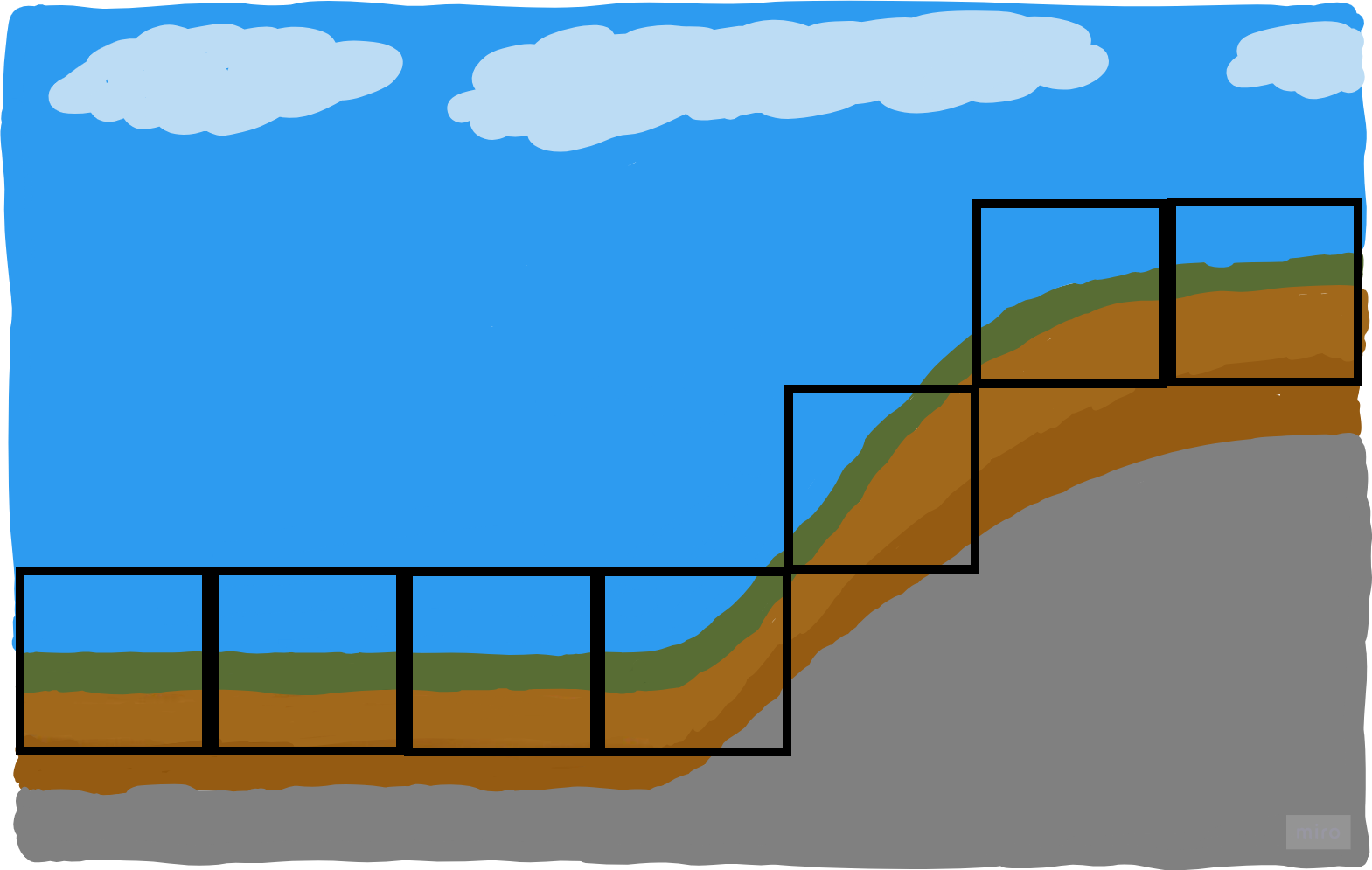
In contrast to the point cloud map, there are no gaps anymore; this representation describes the surface completely. It also means we cannot generate many other worlds anymore that would result in the same map. On the other hand, we have to be more careful in placing such voxels, since they are interpolating the space by design. When we place a 10cm voxel it means 10cm of place is completly occupied by some solid material. So we have to measure this 10cm good enough to be sure about this. Imagine there was a 7cm hole, which we want to avoid since we can get stuck with our small wheels. If we are not careful enough, this would be interpolated by a 10cm voxel.
Representing the Alps world's surface by a triangle mesh using 7 primitives, i.e. lines, could result in the following map:
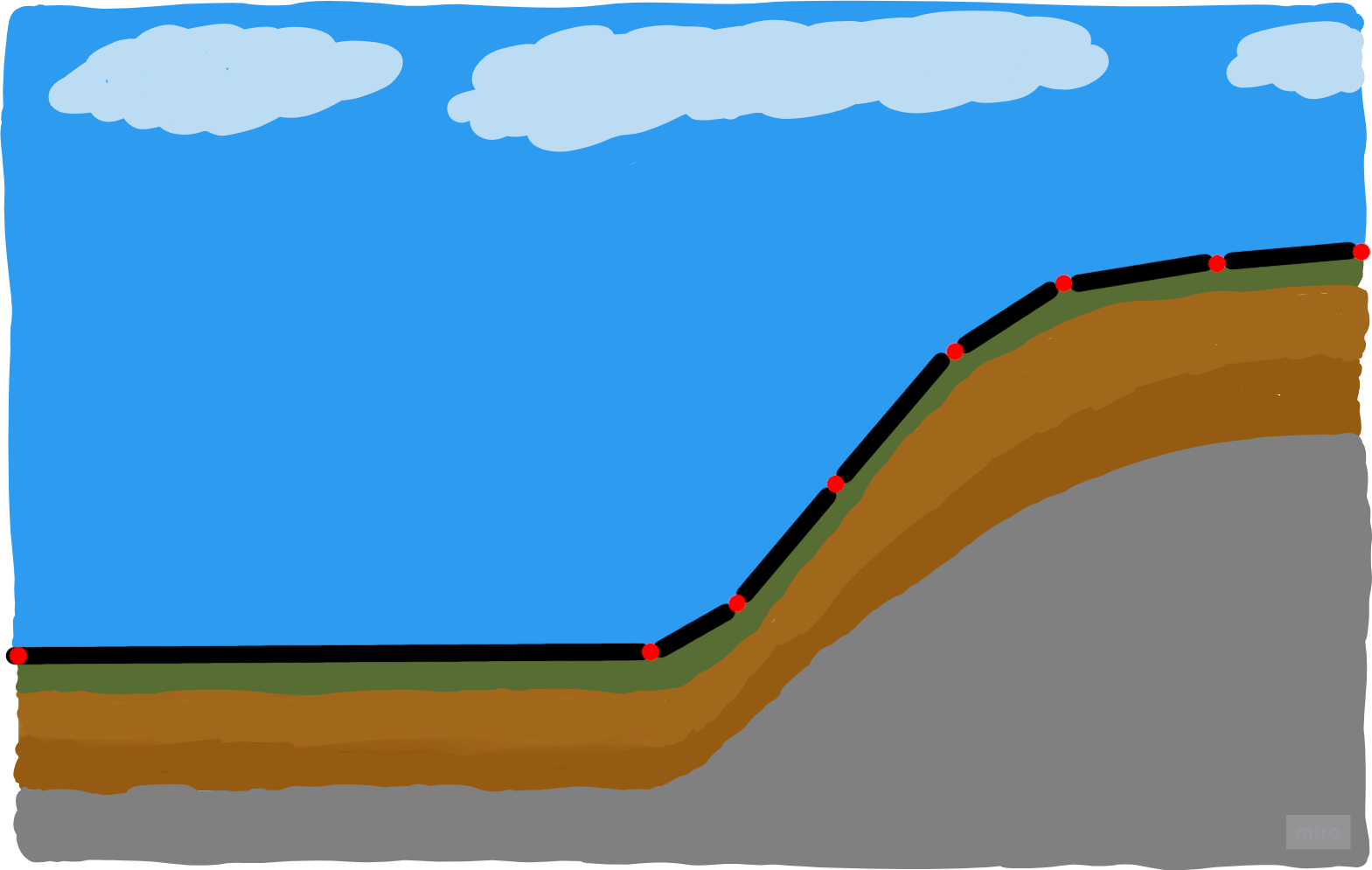
(Red: Vertices, Black: Triangles)
Before giving any explanations: Which of the presented representation would you chose?
In contrast to PCLs, and same as voxel-based maps we can describe the surface completely. Similar to voxel-based approaches we also have to carefully place primitives. An advantage over voxel-based approaches is that we can describe the world more accurately with the same number of primitives. You can see this quality by how the map resembles the real world. Also, consider how many different worlds you can come up with that would result in this map. Not proven, but I guess it's less than for the voxel-based data structure.
The more primitives you "invest", the more accurate a PCL can describe the measured world.
Voxel-based maps accuracy are bound to the minimum voxel size. Normally you choose the voxel resolution application-dependent. The best way of getting the feeling for that is playing Minecraft.
With triangle meshes, we can make use of their inherent adaptive resolution: We can represent planar regions with only a few triangles, and a flat rectangular wall with only two triangles. But for objects or areas with greater detail, we can choose to invest more triangles in order to describe them more accurately.
You can traverse PCLs with some effort. Let's say we want to compute the curvature at a point based on its k-nearest neighbors. Without any prior computation we would first have to figure out all pairwise distances, second sort the points by distance. A smarter option is to construct an additional search structure, e.g. a kd-tree, to accelerate spatial searches. Even after those "smart" changes, the runtime will be not feasible on any robot's hardware. Or in simpler words: When you start to compute the curvature properties for each point of your PCL you will not be able to compute something else during that time. And do not forget: For the additional acceleration structure additional RAM is required. The third option would be to precompute a certain neighborhood for each point. Dependent on the neighborhood size, the required RAM increases exponentially. For the worst-case formula search for "fully-connected graph". In simpler words: If you want to use your RAM for something else, don't do that.
Given a voxel-based map, you can traverse over the neighborhood just by increasing spatial indices, which have a constant runtime or in big-O notation:
Given the same resolution/density, triangle meshes have the same optimal runtime properties as voxel-based maps for neighborhood traversal. However, since in triangle meshes one can skip larger distances over flat regions, you can traverse larger distance in less number of operations.
PCL maps are simpler to handle than voxel-based maps, which are simpler to handle than mesh maps. To handle mesh maps effectively, more knowledge is required. Or in other words, it is easier to handle meshes wrong.
Using triangle meshes we gain more potential advantages:
- We can draw on decades of development in computer graphics; both software and hardware, e.g. RTX units for raycasting or hardware for rendering.
- Textures! We can apply fine-granular information, such as colors, to low-resolution geometries.
Building such maps can be done by many different procedures ranging from hand-modeling, e.g. using CAD programs, to more automatic approaches such as simultaneous localization and mapping (SLAM), photogrammetry, bundle adjustment, .... The next guides give a brief overview how we use software from those categories. However, all methods are very interesting and I strongly recommend to gain deeper knowledge of the actual implementations and the related math.