Building Shapes

Shapes are formed one of four ways within MonkeyCam:

• Basic geometry: given the parameters for a line, arc, ellipse, or Bezier curve generate a path of 2D points.
• Offsetting: given an existing path, grow or shrink the path by a fixed offset.
• Clipping: given two existing paths, apply common boolean operations like and, or, not, xor, etc.
• Deforming: given an existing path in 2D space, define it's Z coordinates based on another path to turn it into a 3D path.

Everything MonkeyCAM does is based on these four simple operations.

Basic Geometry

Let's say we want to generate a arc to represent the sidecut of a snowboard with an effective edge of 136cm and a radius of 10m. How do we generate the points along this arc, and where do we put them?

For now, assume that we'll start the sidecut at (0,0) and end it at (136,0). We know where the center of the board is (in this case, at x=68). There is a simple equation for finding the depth of a chord of a circle: depth = radius - sqrt(radius^2 - (length^2 / 4)) = 2.315 for this case, so the center point of the sidecut of the board is at (68, 2.315). Now we have three points, and we can find the equation of a circle thru three points (see the Circle class), and from there we can find the start and end angles of just the arc we need, and now you have the ArcPath class which creates a ArcPath of 100 Point representing the arc of our sidecut.

An ArcPath object is constructed with three 2D points and a direction (clockwise or counterclockwise). It inherits from Path which is pretty much just a std::vector<Point>, and on construction it sweeps out 100 points to represent the arc thru the three given points, and makes those points available for later use.

The following basic geometry paths are available:

• Path: holds a sequence of any points.
• ArcPath: see above.
• EllipsePath: a half of an ellipse.
• BezierPath: a Bezier Curve between two points, with two control points.

Bezier Curves

Bezier Curves deserve a bit of explanation. MonkeyCam uses them for a wide variety of shapes: nose and tail shapes, smoothing transitions from the sidecut to the inset nose and tail portions of the core, etc. We use simple 4-point Bezier Curves: a start and end point, and two control points. The BezierPath class creates the proper points, making them easy to join up with other paths.

Picking where to put control points can be interesting. Usually the Bezier needs to interface smoothly with other paths around it, and the location of the control points not only control the shape of the curve, but also the angle with which the curve hits it's start/end points. Sometimes we know that the angle has to be 0 or 90 degrees, so we can pick a control point with the same X or Y value as the end point. Other times we have to compute a vector from the start or end point at a specific angle, and use that to constrain where the control points can go. You'll see this considered when we talk about how nose and tail shapes are formed.

Special Paths

There are a few special path types which don't build paths from basic geometry, but build new points from existing points. One is worth calling out now. (The others are very special-purpose and will be discussed with deforming.)

• MirroredPath: a path which mirrors another path across the Y axis, and reverses it. We form our shapes with the Y axis down the center of the long axis of the board, so it's common to, say, form an ArcPath for one side of the board and then mirror it to get the path on the other side.

Forming a Shape

So how do we form the overall shape of a snowboard? We build upon the primitives above. Create two ArcPath for each sidecut. Create two BezierPath for the nose and two for the tail. Ensure the start and end points all line up, then join the paths together into a single path. The joining operation is actually quite easy: create a new Path and call push_back_path(const Path& path) to add the paths in the proper order.

This is a surprisingly simple process repeated many times in MonkeyCAM. See the code to form the Overall Shape for a good example (BoardShape::buildOverallPath()).

Offsetting

Offsetting is the process of growing or shrinking a shape by a fixed amount. Consider a circle of radius 20. If we offset it by 2, we would have a circle at the same center, with a new radius of 22. If we offset if by -2 we would have a circle at the same center with a new radius of 18.

Offsetting is the most important operation needed when building toolpaths. Every shape we build will represent the outline of a final part. But we need to use a CNC machine, likely a CNC router, to cut these parts. Router bits have size... they're not lasers :) We must account for that size by offsetting the actual shape by the radius of the cutter before generating a toolpath.

Many different kinds of cutters can be used, so the radius of each cutter is a parameter to MonkeyCAM.

Offsetting is hard

Offsetting sounds simple, and with the example of a true circle above it is indeed very simple. Just change the radius and you're done. But what about a complex shape, like a snowboard?

There are a number of research papers in the filed of Computational Geometry about offsetting arbitrary polygons. This is something that seems simple on the face of it, but has a number of extremely difficult corner cases. Like many problems in computational geometry even the imprecision of floating point can have drastic effects on the outcome. A great deal of effort was originally spent in MonkeyCAM developing and researching stable offsetting algorithms, but with v4 all of that was tossed aside in favor of Clipper.

Clipper is an open source freeware library for clipping and offsetting lines and polygons, developed by Angus Johnson. It implements a very robust offsetting algorithm which has proven to be significantly more stable than anything previously in MonkeyCAM.

It is worth spending some time looking over Clipper's site. The examples go a long way to showing what can be done with offsetting and clipping.

Offsetting functions

Offsetting is accomplished via a number of helper functions in the PathUtils namespace:

• std::vector<Path> OffsetPath(const Path& path, MCFixed offset): given a Path and an offset value, offset the path and return a collection of new paths.
  • Imagine offsetting an hourglass shape inwards. If you offset it more than the width of the center you'll end up with two separate paths, one for the top and one for the bottom of the hourglass. This happens often with skis and snowboards for the inner-most toolpaths used to profile the top of the core.
• Path OffsetOpenPath(const Path& path, MCFixed offset): given an open Path and an offset value, offset it and return a single new path. This is used for restricted cases where a path is "open" rather than "closed". A closed path is one that starts and ends at the same place, like a circle or a snowboard shape. An open path may be a line, a portion of a circle, a single arc, etc. Offsetting this yields another single open shape.
  • There are obviously cases where an open shape could generate multiple offset paths. However, the specific uses currently in MonkeyCAM do not involve any of these shapes, thus the function returns a single Path. It will assert if this invariant is violated.
• std::vector<Path> OffsetLines(const std::vector<Path>& paths, MCFixed offset): given a set of open paths, and an offset, offset each path and return a set of closed paths. This is used to grow shapes around single lines or simple shapes like arcs. Imagine forming a container for an arc where the sides of the container are all a fixed distance from the arc.

Clipping

"Clipping", in this context, refers to the process of finding the intersection between a subject polygon and a clip polygon, and then applying any one of the common boolean operations on those polygons based on the intersection regions. The Wikipedia page on Boolean operations on polygons is a great reference, and the diagrams down the side will help illustrate.

Other helpful reading about clipping:

• Vatti clipping algorithm
• General clipping in computer graphics
• Constructive geometry: MonkeyCAM uses more primitives, but at it's core it's all constructive geometry.

Why clipping?

Forming the overall shape of a snowboard is easy with the primitives described in Basic Geometry above. Surely it would be easy to form all of the other necessary shapes the same way, and simply offset them when emitting toolpaths. Why not just build the core shape separately from the overall shape?

1. All of the parts of a snowboard must fit together tightly and accurately. Building snowboard parts with a CNC machine is done because of the precision the device brings to the table, not just because of the automation. Building shapes that must fit together well separately is possible, but it is actually surprisingly difficult to do without having lots of subtle errors between the parts. In some cases, these errors don't matter. In other cases, the do quite a lot.
2. A central design principle of MonkeyCAM is that it should be able to operate given a single input shape. Right now (v4.0.3) MonkeyCAM only takes a parametric description of a board. But it generates a single Overall Shape and operates on that for everything else so that in the future we can more easily integrate with other CAD programs to generate the Overall Shape. If MonkeyCAM were to generate the core shape from parameters as well, then it would require a core shape from another CAD program, too, which would be difficult for most people to do due to #1 above.

Thus, all shapes in MonkeyCAM are derived from the Overall Shape via a series of clipping, offsetting, and boolean operations.

Example: Forming the Core Shape

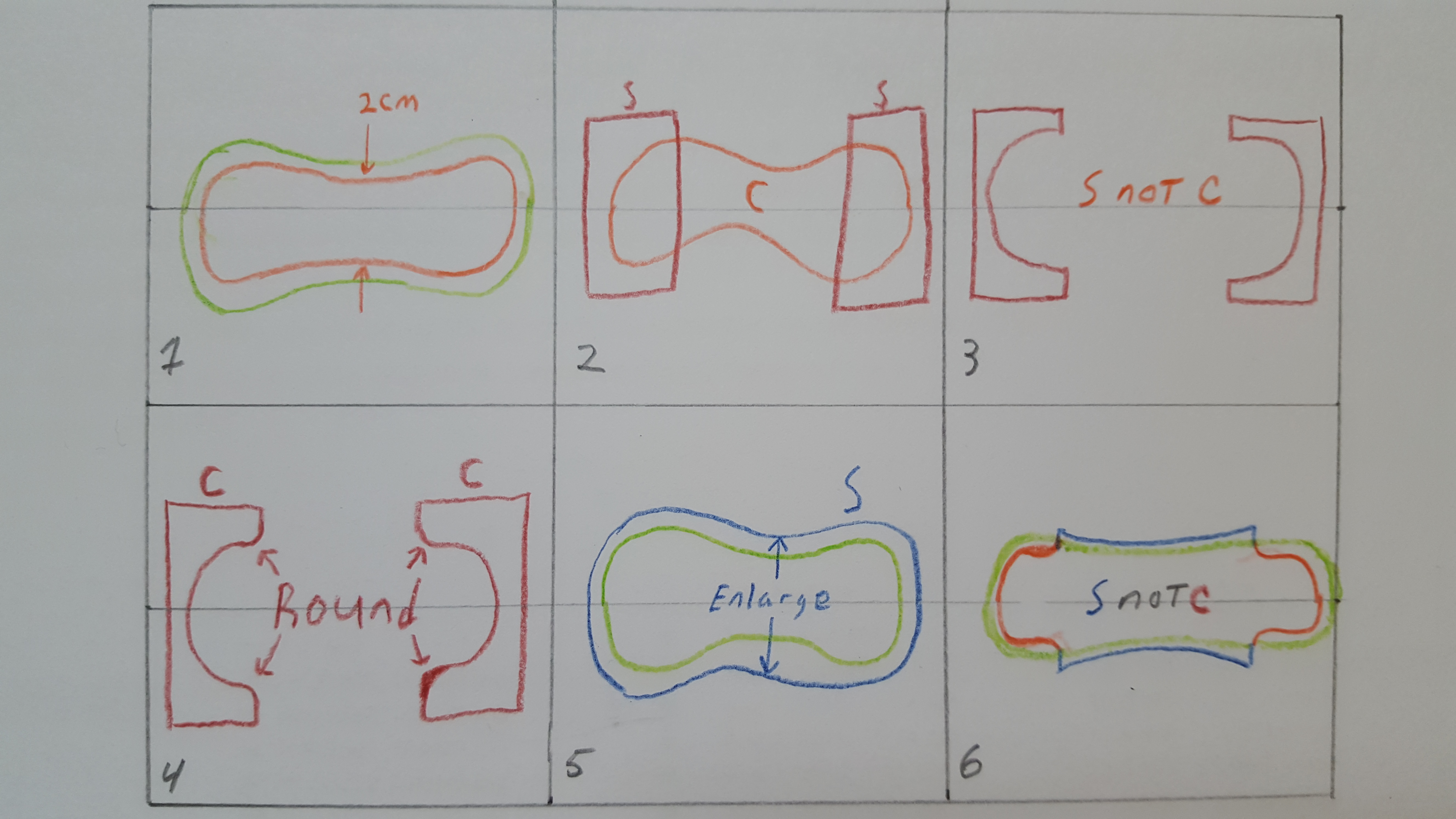
Let's look closely at how the Core Shape is formed from the Overall Shape. This is coded in const Path& BoardShape::buildCorePath(const Machine& machine).

1. Offset the overall path inward (smaller) by the spacer size. The core will have room for nose/tail spacer material at the ends, usually 2cm all the way around, just past the end of the effective edge. Shrinking the overall shape by 2cm shows us exactly what the nose and tail should look like. But the center is useless.
2. Form two squares, one for the nose and one for the tail, which enclose just the nose and tail respectively. These squares are wider than the overall width of the nose and tail, and longer than the nose and tail. They intersect the path from #1 exactly at the ends of the effective edge.
3. Clip the squares from #2 with the area defined by #1. The two squares are the subject polygons (S) and the shrunken snowboard shape from #1 is the clip polygon (C). This leaves us with two polygons, one at the nose and one at the tail, which are the result of the boolean operation S not C. These are the squares formed in #2 with the shrunken snowboard removed. (These actually represent what the nose and tail spacer material would really look like during construction.)
4. Round off the inner corners of each polygon from #3. This rounds off the portions of the spacer at the ends of the effective edge, ensuring a smoother transition which is easier to cut and work with. This is not done via a clipping operation (though it likely should be) though it is done with constructive geometry. See the code in roundSpacerEnds().
5. Offset the Overall Shape outwards by the amount the sidewalls should overhand the edge. This is done to give some alignment tolerance during layup, and is a configurable paramter.
6. Finally, clip the larger snowboard shape from #5 with the spacer paths from #4. The enlarged snowboard shape from #5 is the subject (S) and the two spacer shapes are the clips (C). The result of the boolean operation S not C is a core shape where the sidecut overhangs the base of the board and the nose and tail are inset (with rounded transitions) to allow for room for the nose and tail spacers.

A ghetto illustration of the process:

Deforming

Deforming a path is one of the ways that MonkeyCAM turns a 2D path into a 3D path suitable for machining.

The simplest form of this is a constant adjustment to Z. The Z value of every point in a path is set to a constant value, such as a depth deep enough to cut thru a material on the table without marring the table too badly. This is rarely done to a path ahead of time, and is instead typically applied when actually emitting a G-Code file with GCodeWriter::emitPath(Path& path, MCFixed depth).

More complex deformation can be visualize as draping a 2D path over a 3D surface. The Z values are set to various heights depending on the underlying surface. This is not done literally in MonkeyCAM as there are actually no true 3D surfaces necessary. Any 3D surface is assumed (and required) to be flat on one axis. A good example is the core: it is tapered end-to-end, but flat side-to-side. Thus, the deformation can be accomplished with a single path specifying the desired Z height rather than a true 3D surface. We call this "applying a profile".

This is done with a ProfiledPath, and the constructor ProfiledPath(const Path& path, const Path& profilePath) which applies a height profile to path as described in profilePath. Both are 2D paths. The profilePath represents the height of the profile along the X axis by changing values in the Y axis. In essence, the height profile is drawn as if looking at it from the side. The X values of the profilePath must include every X value in path. The shape in path is deformed with the given profile, adding extra points where necessary to ensure that the Z values are correct everywhere.

This is used in a few places in MonkeyCAM, most notably to generate the G-Code program to apply the thickness profile to the top of the core. A full set of toolpaths are generated to move the cutter over the entirety of the core (successively smaller offsets of the overall shape), then the collection of toolpaths is deformed with a single thickness profile path. See BoardShape::generateTopProfile().