-
Notifications
You must be signed in to change notification settings - Fork 226
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
about how to computer measurements Jacobian #57
Comments
|
Can you please describe how to try to compute the Jacobian ?
En 4 mar. 2021 4:40, en 4:40, chenwinki <[email protected]> escribió:
…Hi, thank you for your really greatful work. I am learing about AI-IMU,
and I encountert a problem about how to computer measurements Jacobian.
I read the sup.pdf #48 which present a example when the measurement is
[<img src="https://latex.codecogs.com/gif.latex?y=R^{T}v"
title="y=R^{T}v" />](url), but the measurement in AI-IMU is more
complicate, I have tried to computer the jacobian for AI-IMU
measurement, but failed, could you please show us more detailed steps.
thanks very much.
--
You are receiving this because you are subscribed to this thread.
Reply to this email directly or view it on GitHub:
#57
|
|
@mbrossar Along the same lines, I wonder in equation (26) in the paper, if the Jacobian of equation (6) i.e., F with respect to the rotation matrix, i.e., F21 where it is equal to (g)_cross should be (lineacc)_cross where lineacc is the linear acceleration. |
Hi, @chenwinki did you figure out how the measurement Jacobian was derived? |
@chenwinki , I think your derivation is correct, and I got the same derivation as yours. The derivation in the sub.pdf seemed to be wrong. |
|
@chenwinki , @Rajat-Arora , below is my derivation result which is implemented in the code. And please refer to the paper of the IEEE version (https://www.researchgate.net/publication/339920913_AI-IMU_Dead-Reckoning), which has an update on the measurement function and its corresponding Jacobian. The measurement function is updated as And the corresponding Jacobian H becomes For H matrix, my derivation has a sign difference on the two submatrics of H. |
@robocar2018 thanks for sharing had seen this post of your's in another issue as well. Is it possible for you to share how you got to the result of this derivation? |






Hi, thank you for your really greatful work. I am learing about AI-IMU, and I encountert a problem about how to computer measurements Jacobian. I read the sup.pdf #48 which present a example when the measurement is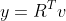 , but the measurement in AI-IMU is more complicate, I have tried to computer the jacobian for AI-IMU measurement, but failed, could you please show us more detailed steps.
, but the measurement in AI-IMU is more complicate, I have tried to computer the jacobian for AI-IMU measurement, but failed, could you please show us more detailed steps.
thanks very much.
The text was updated successfully, but these errors were encountered: