An empirical SFC macroeconomic model for Italy using Bimets package
Authors: Rosa Canelli and Marco Veronese Passarella
Last change: 6 February 2024
Description: This repository contains two types of code. The file named Italy_SFC_model.r replicates the baseline and the experiments discussed in: Canelli, R., Fontana, G., Realfonzo, R. and Veronese Passarella, M. (2022) Is the Italian government debt sustainable? Scenarios after the Covid-19 shock, Cambridge Journal of Economics. Notice that an early version of it was used to produce the simulations discussed in: Canelli, R., Fontana, G., Realfonzo, R. and Veronese Passarella, M. (2021) Are EU policies effective to tackle the Covid-19 crisis? The case of Italy, Review of Political Economy. The other (numbered) files allow replicating the baseline and the experiments discussed in: Canelli, R., Fontana, G., Realfonzo, R. and Veronese Passarella, M. (2024) Energy crisis, economic growth and public finance in Italy, Energy Economics. A detailed description of the latter is provided below.
- 1 Model and data
- 2 Accounting tables
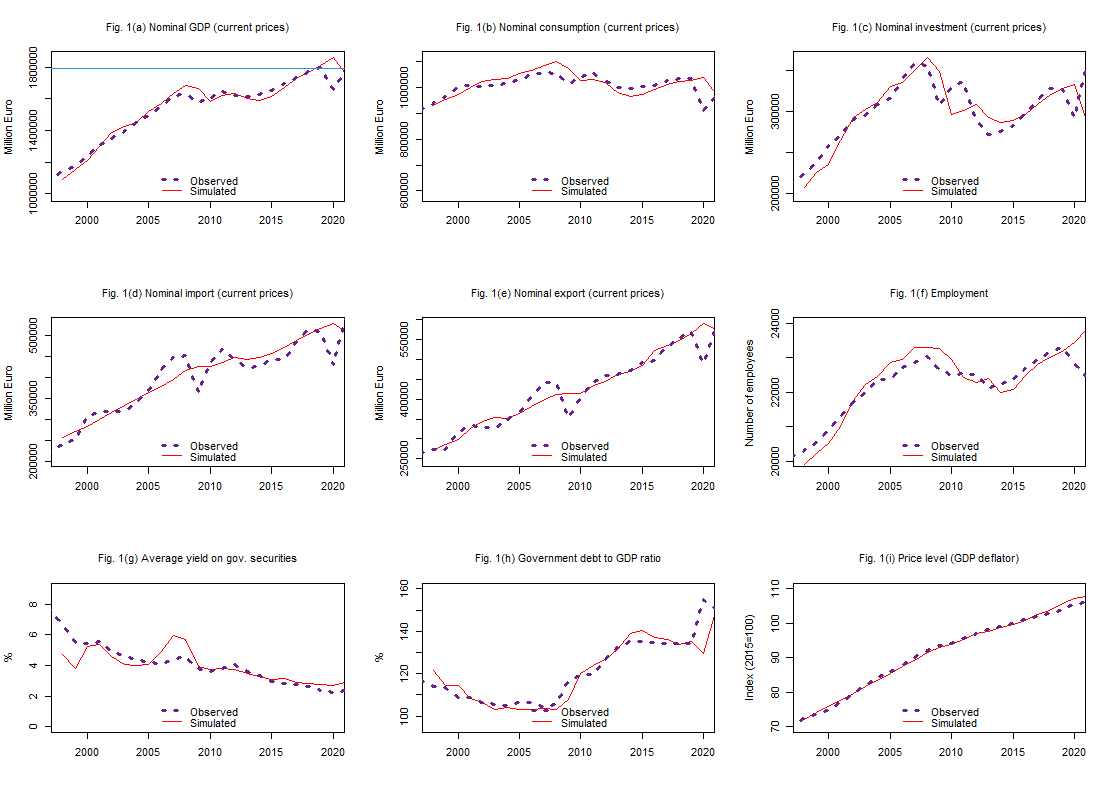
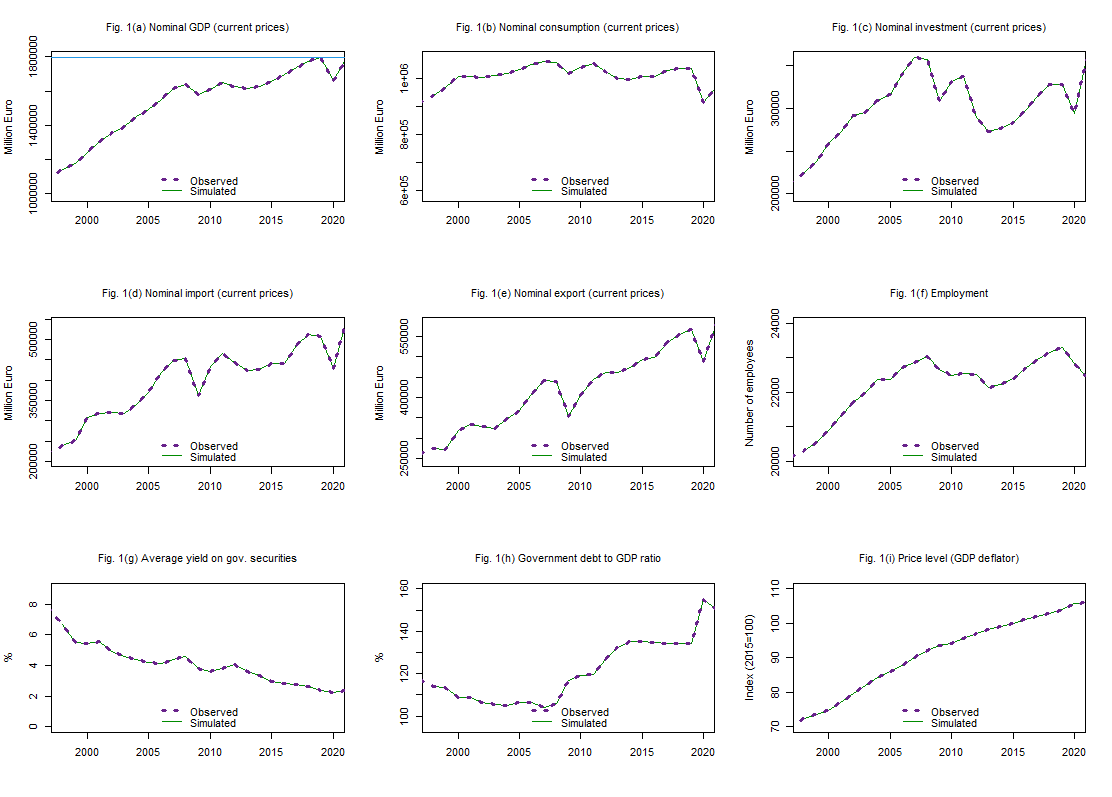
- 3 In-sample predictions
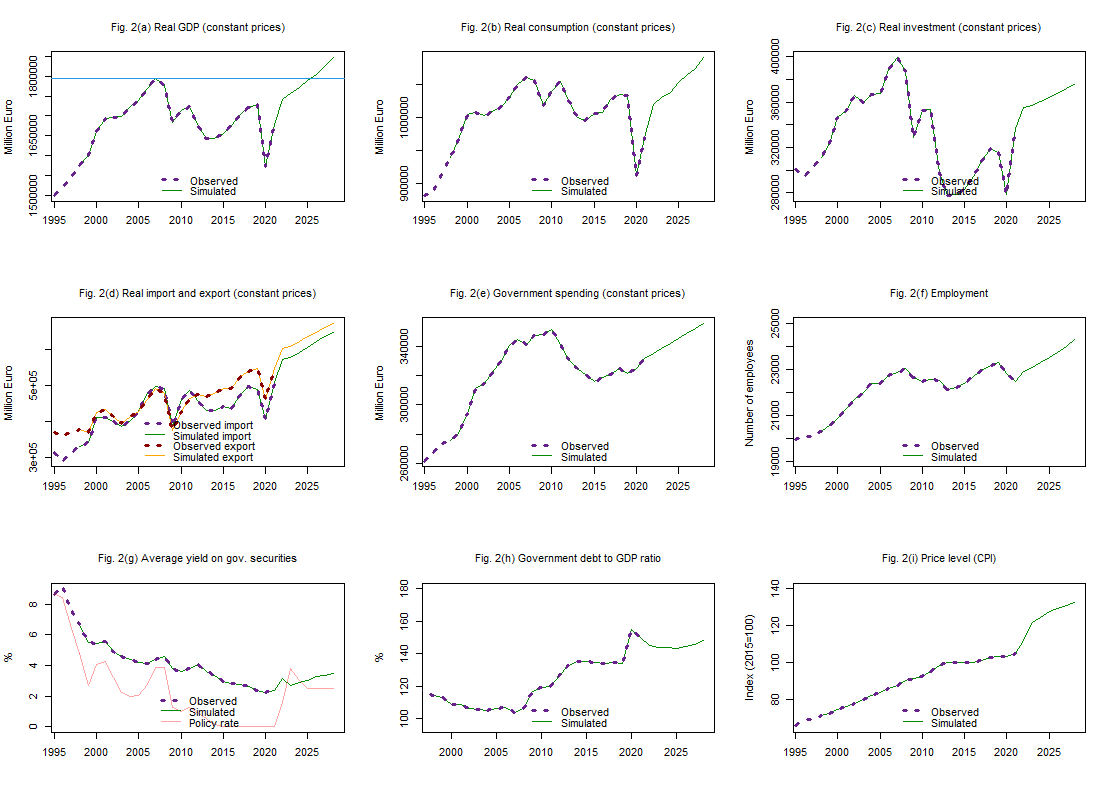
- 4 Out-of-sample predictions
- 5 Model watertightness
- 6 Experiments
- 7 Quick execution
[Warning: work in progress] 🛠️
The model presented here is created using the R package named Bimets. You can install it from the Packages sub-pane within RStudio. We also recommend installing and loading the knitr package.
library(bimets)
library(knitr)Once packages have been loaded, the first step in creating the model is to define the structure of the economy, determining the level of aggregation implied by the desired accounting matrices. Subsequently, the density of the original matrices, as implied by the observed series, must be consistently reduced to limit the number of equations. Additionally, in the absence of information (e.g., on cross-sector interest payments), a decision must be made regarding which sector is paying whom. Available data must be reclassified accordingly - please refer to Veronese Passarella (2019), section 2, for additional information on the method for reclassifying Eurostat time series.
In our model, we consider six sectors (households, production firms, government, commercial banks, central bank, and the foreign sector) and six financial assets (cash, deposits, securities, loans, shares, and other net financial assests). The associated simplified balance sheet of Italy in 2021 is:
Figures are all expressed at current prices, million euros.
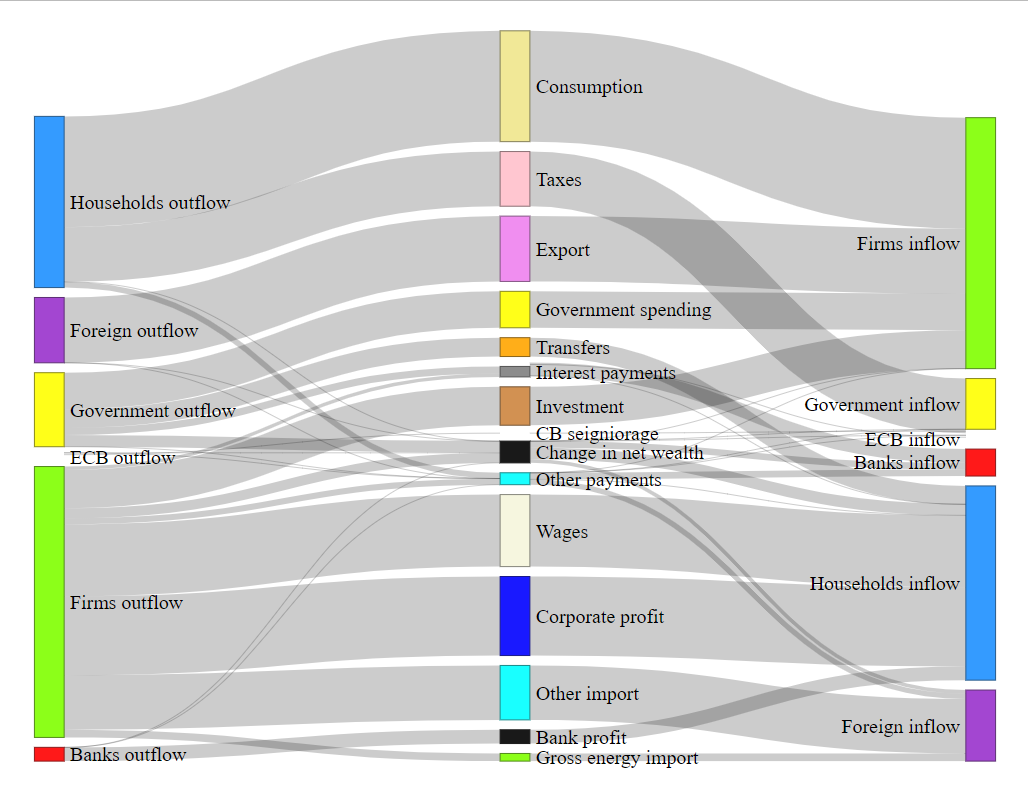
Similarly, the simplified or riclassified transactions-flow matrix of Italy in 2021 is:
where the entry named 'Other payments' allows aligning each sector's saving, calculated based on Eurostat's non-financial transactions, with the change in financial wealth as derived from Eurostat's financial balance sheets.
Note: The R code to create the tables above (using observed series) is presented in Section 2.
The second step to create the model is to import the data (observed series). Our code takes the observed series from a Dropbox folder, containing Eurostat data for Italy over the period 1995-2021.
#Upload data: time series for transactions-flow matrix and balance sheet
DataEE <- read.csv("https://www.dropbox.com/scl/fi/58un32aub0asx1tu1t53c/Data_Aalborg.csv?rlkey=642w2hwa8qo069nmn1rc848i2&dl=1") Running this chunk of code allows creating the dataset used by the model to estimate the coefficients and attribute initial values to the variables. Data are already classified to fit the two tables above.
| Year | CONS | INV | GOV | X | IM | Y | TAX | INVnet | TR | WB | INTh | INTlh | INTgh | INTm | INTf | INTg | INTgb | INTb | INTcb | INTrow | Ff | DIV | FUf | Fb | Fcb | YD | OPh | OPf | OPg | OPb | OPcb | OProw | Yrow | DEF1 | Hh | Hbd | Hs | Mh | Ms | Bh | Deb | Bb | Bcb | Bs | Brow | Lf | Lh | Ls | Eh | Es | OAh | OAf | OAg | OAb | OAcb | OArow | Vh | NVh | Vf | Vg | Vb | Vcb | Vrow | K | Rlh | Rl | Rb | Rstar | Prod | ProdR | Delta | Kappa | KappaN | Py | Pc | Exr | Exr42 | Exr42R | IMen | Pen | Pen2 | Pim | Pim_en | Py_row | RHO | w | gid | gkn | gy | Rbb | Rbrow | Rbh | Re | gw | CPI | PI | PIen | Nd | Ns |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1995 | 581704 | 198068 | 172298 | 243824 | 207651 | 988243 | 304502.9179 | 61690.466 | 32837 | 353786 | 94539 | 22058.98524 | 202553.2366 | -85955.25137 | 32051 | 101685.9999 | -29707.98536 | 110357.2512 | -85955.25137 | 14796 | 594208 | 435525 | 158683 | 110357.2512 | -85955.25137 | 709948 | -12593.3333 | -8198 | -26684.6667 | 108193.2514 | 9950 | -70667.25137 | 11869868.24 | 88273.33333 | 42951 | 3915 | -46866 | 642843 | -642843 | 407396 | 1179962.142 | 390724 | 106668 | -1179962.142 | 275174.142 | -480014 | -166659 | 646673 | 337925 | -337925 | 276065 | 104061 | 239854.142 | -483688 | -80593 | -55699.142 | 1707180 | 1540521 | -713878 | -940108 | -85219 | -20791 | 219475 | 2964729 | 0.13236 | 0.066770969 | 0.086177341 | 0.086875 | 49.59938769 | 75.25206367 | 0.046 | 0.333333333 | 0.34940601 | 65.911 | 65.5 | 1.308 | 77.5 | 92.40989 | 15433.334 | 49.50860467 | 56.1921773 | 64.63870703 | 51.80703164 | 55.27815729 | 0.006090134 | 17.75633015 | 0.037188395 | 0.023283628 | 0.051381348 | -0.076033173 | 0.053769587 | 0.497190048 | 1.288821484 | 0.074269715 | 0.045801527 | 0.045075936 | 0 | 19924.5 | 22560.6 |
| 1996 | 611812 | 202429 | 184246 | 247921 | 200535 | 1045873 | 339106.6832 | 66051.466 | 32914 | 378499 | 96012 | 21362.90615 | 196733.19 | -79358.28384 | 28312 | 108261.0004 | -21732.90575 | 107300.2842 | -79358.28384 | 12619 | 677120 | 514076 | 163044 | 107300.2842 | -79358.28384 | 763826 | -25868.601 | 38058 | -49285.399 | -15041 | 976 | 51161 | 12432671.32 | 65672.601 | 43739 | 4488 | -48227 | 666811 | -666811 | 490407 | 1245634.743 | 439727 | 97545 | -1245634.743 | 217955.743 | -482938 | -176991 | 659929 | 370549 | -370549 | 298020 | 100224 | 190568.743 | -537593 | -69133 | 17913.257 | 1869526 | 1692535 | -753263 | -1055066 | -100260 | -19815 | 235869 | 3030780.466 | 0.128183333 | 0.058624503 | 0.091749554 | 0.084375 | 52.20568342 | 75.79002268 | 0.046 | 0.345083721 | 0.369781837 | 68.882 | 68.5 | 1.27 | 86.1 | 101.71875 | 19682.28 | 51.77617435 | 58.72509228 | 68.18104965 | 54.64617037 | 58.3075213 | 0.006730543 | 18.8931151 | 0.022017691 | 0.022279091 | 0.058315617 | -0.055622142 | 0.045858233 | 0.482904079 | 1.521272472 | 0.064021391 | 0.045801527 | 0.045075936 | 0.045801527 | 20033.7 | 22737.8 |
| 1997 | 645631 | 213028 | 193160 | 263802 | 223262 | 1092359 | 348240.7178 | 73612.09856 | 35143 | 397066 | 79460 | 18600.83965 | 153836.1258 | -55775.28619 | 28260 | 94403.00059 | -10613.83906 | 92022.28678 | -55775.28619 | 6956 | 701730 | 567744 | 133986 | 92022.28678 | -55775.28619 | 914897 | 91702.431 | 34697 | -29706.431 | -41340 | 407 | -55760 | 13182538.9 | 30240.569 | 46923 | 4901 | -51824 | 638201 | -638201 | 559168 | 1275875.312 | 441022 | 92006 | -1275875.312 | 183679.312 | -493212 | -188351 | 681563 | 448317 | -448317 | 457543 | 109224 | 160862.312 | -630885 | -59590 | -37154.312 | 2150152 | 1961801 | -832305 | -1115013 | -141600 | -19408 | 146525 | 3104392.565 | 0.105094833 | 0.057297876 | 0.075787064 | 0.063958333 | 54.29705441 | 76.8524924 | 0.046 | 0.351875279 | 0.377800508 | 70.651 | 69.8 | 1.134 | 87.5 | 100.6284 | 20382.45 | 52.75878788 | 60.23324663 | 71.82719165 | 57.56850286 | 61.42565315 | 0.007679399 | 19.73665636 | 0.052359099 | 0.024288166 | 0.044447079 | -0.024137338 | 0.031914736 | 0.313690722 | 1.532169834 | 0.044648077 | 0.018978102 | 0.0256816 | 0.018978102 | 20118.2 | 22865.7 |
| 1998 | 679941 | 224747 | 199624 | 274042 | 239497 | 1138857 | 363999.2758 | 81944.94203 | 58835 | 395312 | 62467 | 16279.38098 | 122672.1812 | -43925.80025 | 15700 | 85175.00053 | -1030.380451 | 74874.80078 | -43925.80025 | 7459 | 835871 | 745987 | 89884 | 74874.80078 | -43925.80025 | 958284 | -15192.525 | 108026 | -43185.475 | -124795 | -1730 | 76877 | 13879204.32 | 23560.525 | 50305 | 5521 | -55826 | 609760 | -609760 | 513956 | 1299435.837 | 577525 | 78127 | -1299435.837 | 129827.837 | -504062 | -205507 | 709569 | 562925 | -562925 | 708705 | 99819 | 117676.837 | -949250 | -43439 | 66488.163 | 2445651 | 2240144 | -967168 | -1181759 | -266395 | -21138 | 196316 | 3186337.507 | 0.086431083 | 0.031146962 | 0.066758091 | 0.047916667 | 56.0861343 | 77.52271562 | 0.046 | 0.357418823 | 0.384542359 | 72.348 | 71.2 | 1.121 | 90.4 | 102.12797 | 12666.42 | 81.00496309 | 61.68001765 | 74.8634512 | 60.00202299 | 64.02222168 | 0.009054382 | 19.4682229 | 0.055011548 | 0.02639645 | 0.042566592 | -0.002336347 | 0.040608819 | 0.219383408 | 1.663972145 | -0.013600757 | 0.020057307 | 0.024019476 | 0.535383324 | 20305.5 | 23111.2 |
| 1999 | 710248 | 237770 | 206206 | 272643 | 251716 | 1175151 | 356021.3367 | 91198.4747 | 62587 | 410340 | 54993 | 13040.49806 | 115548.0802 | -47514.58213 | 13073 | 71724.00058 | -5035.497487 | 68592.58271 | -47514.58213 | 8726 | 560877 | 558925 | 1952 | 68592.58271 | -47514.58213 | 926019 | 126602.754 | -190861 | 58330.246 | 12396 | -1685 | -4783 | 14675566.04 | 32010.246 | 56333 | 5795 | -62128 | 610642 | -610642 | 438251 | 1331446.083 | 610011 | 75770 | -1331446.083 | 207414.083 | -572790 | -239433 | 812223 | 750109 | -750109 | 840013 | 119913 | 176007.083 | -1071386 | -36465 | -28082.083 | 2695348 | 2455915 | -1202986 | -1155439 | -253999 | -22823 | 179332 | 3277535.981 | 0.06345525 | 0.022823373 | 0.055196262 | 0.027083333 | 57.17411294 | 77.83026537 | 0.046 | 0.358547094 | 0.386592589 | 73.46 | 72.3 | 1.066 | 91.8 | 101.55784 | 16561.2 | 92.65119048 | 62.62804911 | 77.66434745 | 62.24690268 | 66.41751068 | 0.009490012 | 19.96409441 | 0.057945156 | 0.028621725 | 0.031868795 | -0.008719099 | 0.067212088 | 0.224820958 | 0.992894258 | 0.025470815 | 0.015449438 | 0.015370155 | 0.143771776 | 20553.9 | 23279.3 |
| 2000 | 751730 | 259037 | 220195 | 318172 | 307621 | 1241513 | 375224.8494 | 108270.3449 | 66311 | 427487 | 53814 | 16814.76105 | 108571.6979 | -37942.93688 | 17088 | 72578.99948 | -8496.761572 | 63348.93636 | -37942.93688 | 10447 | 780481 | 560823 | 219658 | 63348.93636 | -37942.93688 | 925612 | 129052.913 | -16457 | 14867.087 | -241870 | -274 | 114681 | 17137543.71 | 21803.087 | 59394 | 6644 | -66038 | 631780 | -631780 | 503331 | 1353249.17 | 557289 | 85497 | -1353249.17 | 207132.17 | -641875 | -273340 | 915215 | 747248 | -747248 | 961384 | 146758 | 190874.17 | -1343237 | -42556 | 86776.83 | 2903137 | 2629797 | -1242365 | -1162375 | -495869 | -23097 | 293909 | 3385806.326 | 0.070227417 | 0.026622006 | 0.054511407 | 0.040416667 | 59.46968826 | 79.53044862 | 0.046 | 0.366681635 | 0.397059351 | 74.776 | 74.2 | 0.924 | 88 | 96.48973 | 34898.31 | 94.79664835 | 63.75 | 79.69396408 | 63.8736124 | 68.15321166 | 0.010516319 | 20.47704585 | 0.08944358 | 0.033034068 | 0.056471041 | -0.013928866 | 0.050367843 | 0.24773862 | 0.747655341 | 0.0256937 | 0.026279391 | 0.017914511 | 0.02315629 | 20876.4 | 23418.8 |
| 2001 | 775878 | 271825 | 239959 | 334498 | 318022 | 1304138 | 343517.9719 | 116077.909 | 68186 | 451041 | 52025 | 19920.33585 | 99117.42021 | -27172.08436 | 16530 | 75157.99956 | -7151.336287 | 56471.08392 | -27172.08436 | 10364 | 821681 | 614287 | 207394 | 56471.08392 | -27172.08436 | 720897 | -177595.112 | -14886 | 854.112 | 192428 | -1733 | 932 | 18063016.94 | 66957.112 | 49167 | 8156 | -57323 | 690239 | -690239 | 566966 | 1420206.282 | 534466 | 86879 | -1420206.282 | 231895.282 | -688808 | -303134 | 991942 | 736025 | -736025 | 835553 | 118037 | 191728.282 | -1147766 | -54386 | 56833.718 | 2877950 | 2574816 | -1306796 | -1228478 | -303441 | -24830 | 288729 | 3501884.235 | 0.0728775 | 0.023997979 | 0.055538922 | 0.0425 | 61.21133041 | 79.44880318 | 0.046 | 0.372410369 | 0.40375049 | 77.045 | 75.9 | 0.896 | 89.9 | 97.08403 | 34288.28 | 98.23146825 | 60.81 | 83.42047245 | 66.86035743 | 71.34007175 | 0.011816197 | 21.17016733 | 0.049367465 | 0.034283682 | 0.050442484 | -0.012832366 | 0.050035685 | 0.19692294 | 0.822065767 | 0.033848705 | 0.022911051 | 0.030343961 | 0.036233558 | 21305.5 | 23573.9 |
| 2002 | 798351 | 291267 | 250419 | 329564 | 319342 | 1350259 | 391298.2531 | 130180.3252 | 71440 | 470108 | 46028 | 19814.37917 | 81591.92619 | -15749.54702 | 17230 | 70159.00011 | -9526.379064 | 43267.54713 | -15749.54702 | 13843 | 811498 | 594283 | 217215 | 43267.54713 | -15749.54702 | 858604 | 24775.706 | -51423 | -21476.706 | -59291 | -933 | 108348 | 17984691 | 16469.294 | 53408 | 8970 | -62378 | 716998 | -716998 | 637330 | 1436675.576 | 511446 | 65401 | -1436675.576 | 222498.576 | -716643 | -336487 | 1053130 | 777177 | -777177 | 786643 | 112972 | 170251.576 | -1219280 | -28786 | 178199.424 | 2971556 | 2635069 | -1380848 | -1266424 | -362732 | -25763 | 400698 | 3632064.56 | 0.065365083 | 0.024042654 | 0.04940057 | 0.032083333 | 62.23624958 | 78.21867053 | 0.046 | 0.347 | 0.404172649 | 79.567 | 77.9 | 0.946 | 92.2 | 99.27912 | 32653.125 | 105.7765564 | 63.15 | 86.39226109 | 69.24220501 | 73.88150563 | 0.012510495 | 21.66825684 | 0.071523958 | 0.037174366 | 0.035365122 | -0.017824107 | 0.059695048 | 0.143909734 | 0.807422302 | 0.023527897 | 0.026350461 | 0.032734116 | 0.076809278 | 21695.7 | 23902.1 |
| 2003 | 828304 | 295388 | 264649 | 324994 | 318642 | 1394693 | 393258.1745 | 128313.0302 | 74195 | 490889 | 47510 | 19618.3698 | 90145.08292 | -23016.71312 | 14382 | 66123.00043 | -14327.36938 | 42689.71355 | -23016.71312 | 13322 | 990303 | 724781 | 265522 | 42689.71355 | -23016.71312 | 890185 | -96621.539 | 100881 | 29264.539 | -78778 | -279 | 45533 | 16579854.78 | 34725.539 | 64267 | 8975 | -73242 | 754034 | -754034 | 642341 | 1471401.115 | 511490 | 68819 | -1471401.115 | 248751.115 | -773097 | -371352 | 1144449 | 747473 | -747473 | 860187 | 109856 | 199516.115 | -1352390 | -21619 | 204449.885 | 3068302 | 2696950 | -1410714 | -1271885 | -441510 | -26042 | 453201 | 3760377.591 | 0.0583035 | 0.018603099 | 0.046025005 | 0.0225 | 63.4081062 | 77.25912151 | 0.046 | 0.370891743 | 0.402510012 | 82.072 | 80.1 | 1.131 | 98.4 | 105.94827 | 34191.43 | 105.3707108 | 64.38 | 89.12955539 | 71.43610862 | 76.22240308 | 0.011902646 | 22.31770135 | 0.01414853 | 0.03532785 | 0.032907761 | -0.028013455 | 0.059874541 | 0.141441769 | 0.932581638 | 0.029972162 | 0.028241335 | 0.031482901 | -0.00383682 | 21995.5 | 24141.3 |
| 2004 | 856707 | 308799 | 278255 | 348699 | 340141 | 1452319 | 380777.1062 | 135821.6308 | 74916 | 509540 | 46295 | 20447.26004 | 84747.52034 | -18005.2603 | 14173 | 64586.99987 | -14956.26017 | 37669.26017 | -18005.2603 | 12801 | 1049131 | 882027 | 167104 | 37669.26017 | -18005.2603 | 1041694 | -127976.154 | 120525 | -14715.846 | -22910 | 694 | 44383 | 16589586.29 | 54986.154 | 76070 | 8639 | -84709 | 784680 | -784680 | 718263 | 1526387.269 | 481986 | 74525 | -1526387.269 | 251613.269 | -806836 | -421412 | 1228248 | 857892 | -857892 | 866444 | 112319 | 184800.269 | -1398613 | -15164 | 250213.731 | 3303349 | 2881937 | -1552409 | -1341587 | -464420 | -25348 | 501827 | 3896199.221 | 0.055061667 | 0.017566147 | 0.043894897 | 0.02 | 64.93945681 | 77.06758223 | 0.046 | 0.372752757 | 0.404838856 | 84.263 | 81.9 | 1.244 | 100.4 | 107.67591 | 38846.224 | 96.41309005 | 68.91 | 91.86997485 | 73.632517 | 78.56597314 | 0.011009584 | 22.78373472 | 0.045401303 | 0.036119147 | 0.041318054 | -0.029240572 | 0.051461076 | 0.131935406 | 1.180011853 | 0.020881782 | 0.02247191 | 0.026696072 | -0.085010537 | 22364.2 | 24277.5 |
| 2005 | 885949 | 316194 | 292969 | 367451 | 368928 | 1493635 | 388702.5627 | 136968.8358 | 76130 | 531929 | 47503 | 22393.55976 | 90820.76384 | -20924.20408 | 15074 | 64506.99964 | -16365.56012 | 42026.20372 | -20924.20408 | 10976 | 970860 | 915219 | 55641 | 42026.20372 | -20924.20408 | 1219425 | -4679.641 | 24228 | 9482.641 | 14648 | -8930 | -34749 | 17493109.5 | 65827.641 | 89146 | 8737 | -97883 | 822325 | -822325 | 735715 | 1592214.91 | 499382 | 82215 | -1592214.91 | 274902.91 | -876585 | -479078 | 1355663 | 1057758 | -1057758 | 989547 | 121381 | 194282.91 | -1491229 | -18610 | 204628.09 | 3694491 | 3215413 | -1812962 | -1397932 | -449772 | -34278 | 479531 | 4033168.057 | 0.05313935 | 0.017196279 | 0.042261228 | 0.020208333 | 66.79493773 | 77.70648192 | 0.046 | 0.370337903 | 0.401841653 | 85.958 | 83.7 | 1.244 | 99.3 | 105.95688 | 47940.26 | 75.45 | 76.69 | 94.2 | 75.5 | 80.55857946 | 0.010624753 | 23.78771549 | 0.023947616 | 0.035154474 | 0.028448295 | -0.03395443 | 0.043622501 | 0.126444998 | 1.066823097 | 0.04406568 | 0.021978022 | 0.02011559 | -0.217429916 | 22361.5 | 24238.8 |
| 2006 | 921983 | 340933 | 302522 | 406392 | 419143 | 1552687 | 412935.4616 | 155407.2694 | 84673 | 555830 | 50027 | 26932.7072 | 101583.2882 | -24623.58098 | 19164 | 65618.99958 | -24421.70762 | 46298.58056 | -24623.58098 | 13081 | 681954 | 645212 | 36742 | 46298.58056 | -24623.58098 | 1196782 | 227676.881 | -295739 | 49413.119 | -108750 | -3773 | 131172 | 18391491.59 | 64502.119 | 103968 | 10322 | -114290 | 879188 | -879188 | 735374 | 1656717.029 | 487660 | 93789 | -1656717.029 | 339894.029 | -954392 | -541251 | 1495643 | 1289471 | -1289471 | 1023462 | 126710 | 243696.029 | -1672959 | -17550 | 296640.971 | 4031463 | 3490212 | -2117153 | -1413021 | -558522 | -38051 | 636535 | 4188575.327 | 0.056217792 | 0.020079799 | 0.041212401 | 0.027916667 | 68.3704904 | 77.88491115 | 0.046 | 0.370695733 | 0.403542447 | 87.784 | 85.6 | 1.256 | 99.3 | 105.4757 | 61681.2 | 95.70833333 | 78.98 | 98.4 | 95.7 | 82.64410275 | 0.011740379 | 24.47522886 | 0.078239941 | 0.038532307 | 0.039535763 | -0.04890386 | 0.047584073 | 0.138074238 | 0.609980733 | 0.028902034 | 0.022700119 | 0.021242933 | 0.26850011 | 22709.9 | 24364.2 |
| 2007 | 953816 | 359238 | 307266 | 441837 | 447317 | 1614840 | 465321.4558 | 166563.535 | 78465 | 576340 | 56865 | 34286.6271 | 118836.814 | -27685.1869 | 30044 | 73006.99985 | -45126.62725 | 46889.18675 | -27685.1869 | 26982 | 998664 | 657999 | 340665 | 46889.18675 | -27685.1869 | 679025 | -272211.731 | -9792 | 26685.731 | 144725 | -6743 | 117336 | 18332622.93 | 21101.731 | 112983 | 11364 | -124347 | 915020 | -915020 | 762538 | 1677818.76 | 462908 | 93824 | -1677818.76 | 358548.76 | -1071324 | -602022 | 1673346 | 1199296 | -1199296 | 827606 | 134894 | 270381.76 | -1646395 | -14271 | 427784.24 | 3817443 | 3215421 | -2135726 | -1407437 | -413797 | -44794 | 786333 | 4355138.862 | 0.063347 | 0.028043804 | 0.044067272 | 0.038541667 | 70.68339892 | 78.57203081 | 0.046 | 0.370789555 | 0.40412414 | 89.96 | 87.3 | 1.371 | 101 | 106.39722 | 59734.24 | 94.025 | 86.23 | 98.9 | 94 | 85.39684094 | 0.012419401 | 25.22706282 | 0.053690901 | 0.039766155 | 0.040029317 | -0.092537069 | 0.079383566 | 0.161600511 | 0.510286001 | 0.030718159 | 0.019859813 | 0.024788116 | -0.017588158 | 22846.1 | 24327 |
| 2008 | 973266 | 356666 | 320333 | 439932 | 452498 | 1637699 | 457702.286 | 156329.6124 | 81770 | 595572 | 65938 | 41162.11041 | 147428.9744 | -40328.86402 | 39097 | 76688.00002 | -57908.11039 | 62679.86404 | -40328.86402 | 27496 | 915292 | 562142 | 353150 | 62679.86404 | -40328.86402 | 760338 | -150061.578 | -87738 | -10330.422 | 290011 | -4201 | -37680 | 17674323.9 | 61417.578 | 123257 | 13153 | -136410 | 974991 | -974991 | 809949 | 1739236.338 | 472953 | 105039 | -1739236.338 | 351295.338 | -1134965 | -624988 | 1759953 | 1141864 | -1141864 | 577420 | 137587 | 260051.338 | -1394854 | -17624 | 437419.662 | 3627481 | 3002493 | -2139242 | -1479185 | -123786 | -48995 | 788715 | 4511468.474 | 0.0683731 | 0.034447758 | 0.045706963 | 0.038541667 | 71.08346246 | 77.16398444 | 0.046 | 0.363007967 | 0.394170122 | 92.12 | 90.4 | 1.471 | 103.3 | 107.93314 | 76410 | 122.7666667 | 83.27 | 103.6 | 122.8 | 88.16565515 | 0.013490381 | 25.85048895 | -0.007159599 | 0.035895437 | 0.014155582 | -0.12509637 | 0.07668692 | 0.193339839 | 0.468726653 | 0.024712593 | 0.035509737 | 0.024010671 | 0.305681114 | 23039.1 | 24703.4 |
| 2009 | 953184 | 307703 | 326155 | 353292 | 363078 | 1577256 | 410194.439 | 100175.4502 | 99915 | 590431 | 45050 | 29728.59587 | 92382.19295 | -17603.59708 | 17698 | 66364.99993 | -29036.59594 | 35993.59701 | -17603.59708 | 20623 | 1017050 | 564863 | 452187 | 35993.59701 | -17603.59708 | 905176 | -20882.158 | 47923 | -17766.842 | 65986 | -11416 | -63844 | 17578903.82 | 99844.158 | 129192 | 11664 | -140856 | 994220 | -994220 | 779292 | 1839080.496 | 609381 | 119299 | -1839080.496 | 331108.496 | -1146281 | -654677 | 1800958 | 997363 | -997363 | 709095 | 148886 | 242284.496 | -1485583 | -38854 | 424171.504 | 3609162 | 2954485 | -1994758 | -1596796 | -57800 | -60411 | 755280 | 4611643.924 | 0.047566667 | 0.015439495 | 0.038157551 | 0.012291667 | 69.6378712 | 74.34701087 | 0.046 | 0.342015998 | 0.366467855 | 93.666 | 91.1 | 1.395 | 105.1 | 109.31352 | 52081.4 | 88.21666667 | 84.81 | 94.6 | 88.2 | 90.05561801 | 0.01173181 | 26.06828437 | -0.137279696 | 0.022204622 | -0.036907271 | -0.061394253 | 0.05870559 | 0.114059272 | 0.494685006 | 0.008425195 | 0.007743363 | 0.016782458 | -0.281428184 | 22649.4 | 24556 |
| 2010 | 978454 | 331599 | 331166 | 404013 | 433952 | 1611280 | 421807.5657 | 119463.3795 | 107096 | 599034 | 34172 | 26394.39438 | 59409.22375 | 1157.170637 | 10465 | 66268.00032 | -14186.39406 | 21515.82969 | 1157.170637 | 19888 | 1013316 | 613378 | 399938 | 21515.82969 | 1157.170637 | 880005 | -73383.264 | 11535 | 71182.264 | 4682 | -22786 | 8770 | 18852954.48 | 81565.264 | 133437 | 11172 | -144609 | 988877 | -988877 | 732051 | 1920645.76 | 638344 | 151353 | -1920645.76 | 398897.76 | -1154988 | -686301 | 1841289 | 915991 | -915991 | 771981 | 144560 | 313466.76 | -1555046 | -89941 | 414979.24 | 3542337 | 2856036 | -1926419 | -1607179 | -53118 | -83197 | 813877 | 4731107.304 | 0.040316667 | 0.0090607 | 0.036033224 | 0.01 | 71.70039693 | 76.21620721 | 0.046 | 0.340571434 | 0.366240927 | 94.075 | 92.6 | 1.326 | 101 | 104.33731 | 66130.02 | 105.6083333 | 94.19 | 99.5 | 105.6 | 91.06593797 | 0.011297664 | 26.65643189 | 0.077659301 | 0.025904728 | 0.021571641 | -0.023280007 | 0.060064904 | 0.076234869 | 0.614999754 | 0.022561804 | 0.016465423 | 0.004366579 | 0.197147175 | 22472.4 | 24528.1 |
| 2011 | 1007661 | 337468 | 326718 | 443061 | 466151 | 1648757 | 454145.6216 | 119837.064 | 110671 | 608088 | 38915 | 31564.12683 | 66948.11742 | 3531.009403 | 12701 | 73204 | -20791.12682 | 19942.9906 | 3531.009403 | 23516 | 1174074 | 792739 | 381335 | 19942.9906 | 3531.009403 | 917706 | -198504.369 | 146106 | 105275.369 | 111366 | -12726 | -151517 | 18926146.73 | 52916.369 | 141838 | 11535 | -153373 | 984230 | -984230 | 743323 | 1973562.129 | 523412 | 176406 | -1973562.129 | 530421.129 | -1175094 | -704239 | 1879333 | 844950 | -844950 | 755979 | 137492 | 418742.129 | -1371802 | -118956 | 178544.871 | 3470320 | 2766081 | -1882552 | -1554820 | 58248 | -95923 | 708966 | 4850944.368 | 0.045991667 | 0.010808497 | 0.038114264 | 0.0125 | 73.13020337 | 76.50643222 | 0.046 | 0.339883716 | 0.365296473 | 95.587 | 95.3 | 1.392 | 101.6 | 104.48254 | 76271.13 | 133.8916667 | 103.32 | 107.7 | 133.9 | 92.94986771 | 0.011719822 | 26.97159078 | 0.017699088 | 0.025329602 | 0.023259148 | -0.032570412 | 0.058952449 | 0.091452805 | 0.865444093 | 0.011822996 | 0.029157667 | 0.016072283 | 0.267813462 | 22545.5 | 24606.8 |
| 2012 | 995710 | 288966 | 321754 | 460981 | 443052 | 1624359 | 436848.3013 | 65822.55909 | 120511 | 600264 | 37724 | 36778.88178 | 69509.18801 | 4993.693761 | 12686 | 80829.00101 | -16705.88076 | 27765.30725 | 4993.693761 | 23032 | 1032254 | 808402 | 223852 | 27765.30725 | 4993.693761 | 1280778 | 122959.994 | 20845 | -161315.994 | -83650 | -3494 | 104655 | 20616647.33 | 81252.006 | 137756 | 13380 | -151136 | 1046373 | -1046373 | 736578 | 2054814.135 | 746424 | 192181 | -2054814.135 | 379631.135 | -1161701 | -697100 | 1858801 | 912080 | -912080 | 915462 | 126115 | 257426.135 | -1597634 | -140462 | 439092.865 | 3748249 | 3051149 | -1947666 | -1797388 | -25402 | -99417 | 818724 | 4916766.927 | 0.052225 | 0.010920194 | 0.040955894 | 0.00875 | 72.15909697 | 74.3402396 | 0.046 | 0.330371365 | 0.351000189 | 97.066 | 98.4 | 1.285 | 99 | 102.51107 | 83664.24 | 150.1916667 | 108.71 | 111 | 150.2 | 93.74142715 | 0.012787027 | 26.66560051 | -0.143723257 | 0.01356902 | -0.014797814 | -0.031917267 | 0.043422101 | 0.093511418 | 0.95674537 | -0.01134491 | 0.032528856 | 0.015472815 | 0.121740213 | 22510.8 | 25201.8 |
| 2013 | 982190 | 272433 | 319441 | 461783 | 423095 | 1612752 | 455823.3594 | 46261.72137 | 131490 | 594339 | 37854 | 35859.98583 | 85903.61056 | -12189.62473 | 11661 | 74784.99964 | -23152.9862 | 36557.62437 | -12189.62473 | 24224 | 910531 | 727101 | 183430 | 36557.62437 | -12189.62473 | 1111389 | 39870.735 | -96221 | -5962.735 | -118788 | 30741 | 150360 | 20727022.91 | 82082.265 | 139992 | 13043 | -153035 | 1076752 | -1076752 | 643794 | 2136896.4 | 965725 | 187388 | -2136896.4 | 339989.4 | -1106952 | -684676 | 1791628 | 1036255 | -1036255 | 968231 | 106538 | 251463.4 | -1837834 | -103029 | 614630.6 | 3865024 | 3180348 | -2036669 | -1885433 | -144190 | -68676 | 954620 | 4963028.648 | 0.051441667 | 0.010534332 | 0.036395019 | 0.005416667 | 72.85619418 | 74.20675716 | 0.046 | 0.324953192 | 0.343826695 | 98.18 | 99.7 | 1.328 | 101.7 | 104.41029 | 72200.4 | 141.8083333 | 108.7 | 108.3 | 141.8 | 95.63143633 | 0.012113281 | 26.8493095 | -0.057214344 | 0.009408972 | -0.007145588 | -0.031018545 | 0.063809308 | 0.116625273 | 0.797189939 | 0.006889362 | 0.013211382 | 0.011476727 | -0.055817567 | 22136.1 | 25204.8 |
| 2014 | 986310 | 275995 | 317979 | 473719 | 426597 | 1627406 | 487469.4046 | 47695.68219 | 142072 | 595991 | 35086 | 33320.89867 | 91045.6278 | -22638.72913 | 8050 | 71390.99944 | -21486.89923 | 42522.72857 | -22638.72913 | 24471 | 1090953 | 814731 | 276222 | 42522.72857 | -22638.72913 | 1135780 | -7153.324 | 67588 | -144554.676 | -39772 | -9189 | 133081 | 21619705.53 | 66611.324 | 141353 | 12882 | -154235 | 1110770 | -1110770 | 536907 | 2203507.724 | 1273284 | 202850 | -2203507.724 | 190466.724 | -1082212 | -679562 | 1761774 | 1057339 | -1057339 | 1163011 | 103109 | 106908.724 | -2121132 | -126480 | 874583.276 | 4009380 | 3329818 | -2036442 | -2096599 | -183962 | -77865 | 1065050 | 5010724.33 | 0.048666667 | 0.007438469 | 0.033408732 | 0.001583333 | 73.27027149 | 73.95285635 | 0.046 | 0.324784581 | 0.343716797 | 99.077 | 99.9 | 1.329 | 103.4 | 104.6746 | 51756.01 | 130.5583333 | 101.85 | 104.9 | 130.6 | 97.87056077 | 0.01159736 | 26.83314574 | 0.013074774 | 0.009610197 | 0.009086332 | -0.022249501 | 0.071975773 | 0.141420435 | 0.786226363 | -0.000602018 | 0.002006018 | 0.00913628 | -0.079332432 | 22211 | 25447 |
| 2015 | 1005936 | 283186 | 316344 | 491905 | 442016 | 1655355 | 506679.773 | 52692.68081 | 141366 | 609506 | 28901 | 28060.81389 | 76995.17867 | -20033.36478 | 5335 | 65123.99918 | -13475.8147 | 39953.36396 | -20033.36478 | 21638 | 928480 | 694646 | 233834 | 39953.36396 | -20033.36478 | 1134133 | 126440.409 | -112034 | -22738.409 | 9458 | 951 | -2077 | 25354512.33 | 36187.591 | 144595 | 11845 | -156440 | 1137500 | -1137500 | 420995 | 2239695.315 | 1361780 | 289731 | -2239695.315 | 167189.315 | -1059755 | -679918 | 1739673 | 1154348 | -1154348 | 1280495 | 128309 | 84170.315 | -2150302 | -210205 | 867532.685 | 4137933 | 3458015 | -2085794 | -2155525 | -174504 | -76914 | 1034722 | 5063417.011 | 0.0412925 | 0.005034182 | 0.029554695 | 0.0005 | 73.91660601 | 73.91660601 | 0.046 | 0.326924485 | 0.346291842 | 100 | 100 | 1.11 | 100 | 100 | 44458.08 | 100.0083333 | 95.9 | 100 | 100 | 100 | 0.010413187 | 27.21628585 | 0.02605482 | 0.010515981 | 0.017173957 | -0.010583511 | 0.113605146 | 0.143405056 | 0.656975672 | 0.014278613 | 0.001001001 | 0.009315987 | -0.233995021 | 22394.9 | 25428.2 |
| 2016 | 1019579 | 297798 | 322650 | 497339 | 441578 | 1695788 | 492490.8411 | 64880.81749 | 145038 | 625000 | 22308 | 23771.06648 | 53680.81605 | -7601.749576 | 5205 | 63428.00057 | 1081.934091 | 37659.75014 | -7601.749576 | 16267 | 1119880 | 752840 | 367040 | 37659.75014 | -7601.749576 | 1023768 | -66586.909 | 54297 | 41327.909 | 150612 | -9643 | -170007 | 25801943.97 | 46226.909 | 150624 | 11441 | -162065 | 1182519 | -1182519 | 363801 | 2285922.224 | 1315743 | 417139 | -2285922.224 | 189239.224 | -1039509 | -686157 | 1725666 | 1126524 | -1126524 | 1324893 | 149481 | 125498.224 | -1894223 | -341631 | 635981.776 | 4148361 | 3462204 | -2016552 | -2160424 | -23892 | -86557 | 825221 | 5128297.829 | 0.034961667 | 0.005007172 | 0.028319924 | 0.0000833 | 74.77711781 | 73.93865348 | 0.046 | 0.330672683 | 0.351058495 | 101.134 | 99.9 | 1.107 | 102.1 | 100.84031 | 36762.5 | 80.675 | 98.35 | 96 | 80.7 | 102.3973588 | 0.009675109 | 27.55987106 | 0.051598596 | 0.012813643 | 0.024425576 | 0.0007945 | 0.097296888 | 0.127509391 | 0.65217768 | 0.012624251 | -0.001 | 0.01134 | -0.193317223 | 22677.9 | 25689.9 |
| 2017 | 1046342 | 313526 | 327002 | 533720 | 483997 | 1736593 | 493832.7575 | 77624.29988 | 142440 | 642230 | 21320 | 20590.42798 | 46722.17343 | -4811.745452 | 3572 | 62428.001 | 8671.573029 | 37645.74646 | -4811.745452 | 11846 | 1006081 | 689357 | 316724 | 37645.74646 | -4811.745452 | 1218330 | 179170.011 | -84710 | 39424.989 | -57156 | 1275 | -78004 | 26323897.53 | 42848.989 | 155752 | 12001 | -167753 | 1206658 | -1206658 | 330574 | 2328771.213 | 1248226 | 523682 | -2328771.213 | 226289.213 | -1009435 | -697152 | 1706587 | 1157381 | -1157381 | 1480979 | 153462 | 164923.213 | -1841204 | -441211 | 483050.787 | 4331344 | 3634192 | -2013354 | -2163848 | -81048 | -85282 | 709340 | 5205922.128 | 0.030008333 | 0.003538613 | 0.027309766 | 0 | 75.6682106 | 74.27991891 | 0.046 | 0.333580287 | 0.354957562 | 101.869 | 101.3 | 1.13 | 103.4 | 101.39634 | 52193.31 | 95.65 | 101.25 | 99.4 | 95.7 | 103.8605307 | 0.009945652 | 27.98375606 | 0.052814324 | 0.015136465 | 0.02406256 | 0.006590628 | 0.062598016 | 0.128427831 | 0.611932813 | 0.015380515 | 0.014014014 | 0.007267586 | 0.18562132 | 22950.1 | 25857 |
| 2018 | 1066167 | 328194 | 334454 | 555394 | 512818 | 1771391 | 480055.6522 | 88721.58209 | 141572 | 665490 | 16570 | 18683.6736 | 29951.57742 | 5302.096182 | 1934 | 61354.9994 | 16425.3258 | 31740.90322 | 5302.096182 | 9676 | 1326322 | 907171 | 419151 | 31740.90322 | 5302.096182 | 863136 | -419352.251 | 222355 | 99226.251 | 220437 | -3082 | -119584 | 26726264.67 | 52023.251 | 162421 | 12232 | -174653 | 1224330 | -1224330 | 313141 | 2380794.464 | 1202244 | 541877 | -2380794.464 | 323532.464 | -1018031 | -711907 | 1729938 | 1075545 | -1075545 | 1367631 | 171179 | 264149.464 | -1580695 | -455588 | 233323.536 | 4143068 | 3431161 | -1922397 | -2116645 | 139389 | -88364 | 556856 | 5294643.711 | 0.0268 | 0.001899746 | 0.026346512 | 0 | 76.53979104 | 74.34151252 | 0.046 | 0.334562833 | 0.356671486 | 102.957 | 102.5 | 1.181 | 106.7 | 103.37155 | 59646.3 | 115.1333333 | 106.79 | 102.4 | 115.1 | 106.2717832 | 0.00999077 | 28.75506624 | 0.046783999 | 0.017042434 | 0.020038086 | 0.013158936 | 0.04275944 | 0.090604758 | 0.783813627 | 0.027562782 | 0.011846002 | 0.010680384 | 0.203694023 | 23143.4 | 25898.9 |
| 2019 | 1074680 | 327703 | 334512 | 567784 | 508031 | 1796648 | 506154.8658 | 84149.38931 | 146882 | 681104 | 14113 | 18527.37968 | 29505.85369 | 3134.525981 | 3429 | 56871.99979 | 12795.62011 | 31617.4738 | 3134.525981 | 11436 | 1082293 | 869739 | 212554 | 31617.4738 | 3134.525981 | 1426904 | 189603.392 | -29822 | -124910.392 | -98786 | -18379 | 82294 | 28774461.9 | 28976.608 | 165890 | 12654 | -178544 | 1286064 | -1286064 | 289695 | 2409771.072 | 1370663 | 573547 | -2409771.072 | 175866.072 | -995791 | -728244 | 1724035 | 1228692 | -1228692 | 1541288 | 186937 | 139239.072 | -1780685 | -501746 | 414966.928 | 4511629 | 3783385 | -2037546 | -2270532 | 40603 | -106743 | 590833 | 5378793.1 | 0.026025 | 0.003443494 | 0.023887824 | 0 | 77.17560137 | 74.26229167 | 0.046 | 0.334024374 | 0.3556951 | 103.923 | 103.2 | 1.12 | 105.8 | 101.08213 | 55150.68 | 108.25 | 107.02 | 101.5 | 108.3 | 108.7763154 | 0.009839324 | 29.25704467 | -0.001496066 | 0.015893305 | 0.014258286 | 0.010643114 | 0.035347303 | 0.094225457 | 0.808649568 | 0.017457043 | 0.006829268 | 0.009382558 | -0.059785755 | 23280 | 25861.5 |
| 2020 | 963726 | 293530 | 343580 | 488941 | 429156 | 1660621 | 428608.9298 | 46105.51741 | 202196 | 642972 | 10558 | 16955.9478 | 19250.6187 | 8263.329099 | 3779 | 54290.99891 | 16112.05111 | 28583.66981 | 8263.329099 | 10665 | 1126688 | 801632 | 325056 | 28583.66981 | 8263.329099 | 1149580 | -107752.74 | 112818 | -91533.26 | 130876 | -14959 | -29449 | 26993213.3 | 163194.74 | 185433 | 11474 | -196907 | 1371058 | -1371058 | 263335 | 2572965.812 | 1443952 | 764972 | -2572965.812 | 100706.812 | -1041503 | -736292 | 1777795 | 1234134 | -1234134 | 1651571 | 269617 | 47705.812 | -1690684 | -689767 | 411557.188 | 4705531 | 3969239 | -2006020 | -2525260 | 171479 | -121702 | 512264 | 5424898.617 | 0.023283333 | 0.00362841 | 0.022529526 | 0 | 72.73822717 | 68.88024466 | 0.046 | 0.306110974 | 0.323621459 | 105.601 | 103 | 1.142 | 108.1 | 101.91719 | 31741.38 | 78.45 | 99.6 | 96.3 | 78.5 | 111.9985301 | 0.00836872 | 28.16334576 | -0.1042804 | 0.008571722 | -0.075711547 | 0.011754933 | 0.060642737 | 0.066451332 | 0.652427134 | -0.037382413 | -0.001937984 | 0.01614657 | -0.275288684 | 22830.1 | 25140.6 |
| 2021 | 1030124 | 357215 | 352718 | 582192 | 540198 | 1782051 | 483365.7672 | 107669.6636 | 188601 | 692915 | 10905 | 14916.66234 | 12622.01724 | 13199.6451 | 2326 | 60678.00031 | 25091.33797 | 29134.35521 | 13199.6451 | 9765 | 1141970.282 | 738858.2821 | 403112 | 29134.35521 | 13199.6451 | 1116373 | -60674.87011 | 55160.28211 | 275576.588 | -151307 | -5171 | -113584 | 29441497.75 | 105431.588 | 200683 | 10817 | -211500 | 1428434 | -1428434 | 233263 | 2678397.4 | 1366294 | 868289 | -2678397.4 | 210551.4 | -871902 | -763488 | 1635390 | 1372850 | -1372850 | 1583746 | 284629 | 323282.4 | -1563895 | -783662 | 155899.6 | 4818976 | 4055488 | -1960123 | -2355115 | 20172 | -126873 | 366451 | 5532568.281 | 0.020259167 | 0.002667731 | 0.023582902 | 0 | 79.33378445 | 74.72335354 | 0.046 | 0.322101944 | 0.344334175 | 106.17 | 105 | 1.183 | 109.3 | 101.53931 | 64858.995 | 112.4833333 | 125.39 | 105 | 85.59190031 | 114.2006256 | 0.007572628 | 30.84736029 | 0.216962491 | 0.019847314 | 0.073123247 | 0.01737685 | 0.096964642 | 0.047931408 | 0.598685623 | 0.095301693 | 0.019417476 | 0.005388207 | 0.433821967 | 22462.7 | 24829.5 |
Alternatively, simply copy and paste the https address into your browser, save the dataset in the chosen folder, and set the directory path accordingly.
The third step is to create a text file (txt) defining model equations. For a comprehensive description of the behavioral assumptions underlying the behavioral equations, please refer to Canelli, Fontana, Realfonzo, and Veronese Passarella (2024).
Note: we place the key behavioral equations at the end of the code. This arrangement is intentional, as, after estimating model coefficients, the related details are to be read in a 'last in, first out' order from the RStudio Console.
S_model.txt="MODEL
COMMENT> FIRMS SECTOR ----------------------------------------------------------
COMMENT> GDP
IDENTITY> y
EQ> y = cons + id + gov + nx
COMMENT> Growth rate of nominal GDP (auxiliary)
IDENTITY> gy
EQ> gy = (y/TSLAG(y,1))-1
COMMENT> Depreciation rate (average value over the period 1996-2019)
IDENTITY> deltak
EQ> deltak = 0.046
COMMENT> Real investment net of capital depreciation
IDENTITY> idR
EQ> idR = exp(LidR)
COMMENT> Nominal investment including capital depreciation
IDENTITY> id
EQ> id = idR*p/100 + deltak*TSLAG(k,1)
COMMENT> Nominal capital stock
IDENTITY> k
EQ> k = TSLAG(k,1)*(1 - deltak) + id
COMMENT> Firms' profit
IDENTITY> ff
EQ> ff = y - intf - wb + opf
COMMENT> Interest payments on loans to firms
IDENTITY> intf
EQ> intf = rl*lf
COMMENT> Interest rate on loans to firms
IDENTITY> rl
EQ> rl = rstar + mul
COMMENT> Firms' undistributed profit
BEHAVIORAL> fuf
TSRANGE 1998 1 2021 1
EQ> fuf = theta*ff
COEFF> theta
STORE> coe(3)
COMMENT> Firms' distributed profit
IDENTITY> fdf
EQ> fdf = ff - fuf
COMMENT> Firms' demand for bank loans
IDENTITY> lf
EQ> lf = TSLAG(lf,1) + id - fuf - (es-TSLAG(es,1)) + (oaf-TSLAG(oaf,1))
COMMENT> Supply of shares
IDENTITY> es
EQ> es = eh
COMMENT> Total wealth accumulated by firms
IDENTITY> vf
EQ> vf = oaf - (lf + es)
COMMENT> HOUSEHOLD SECTOR ------------------------------------------------------
COMMENT> Disposable income
IDENTITY> yd
EQ> yd = wb - tax + tr + inth + fdf + fb + oph
COMMENT> Real consumption
IDENTITY> consR
EQ> consR = exp(LconsR)
COMMENT> Nominal consumption
IDENTITY> cons
EQ> cons = consR*p/100
COMMENT> Net wealth of households
IDENTITY> vh
EQ> vh = TSLAG(vh,1) + yd - cons
COMMENT> Loans to households
BEHAVIORAL> lh
TSRANGE 1998 1 2021 1
EQ> TSDELTALOG(lh,1) = phi1*TSLAG(cons/yd,1)
COEFF> phi1
STORE> coe(6)
COMMENT> Interests paid by households on personal loans
IDENTITY> intlh
EQ> intlh = rlh*TSLAG(lh,1)
COMMENT> Premium on government bills held by households
BEHAVIORAL> mubh
TSRANGE 1998 1 2021 1
EQ> mubh = mubh1*TSLAG(mubh,1) + mubh2*mub
COEFF> mubh1 mubh2
STORE> coe(7)
COMMENT> Interest rate received households on their government debt holdings
IDENTITY> rbh
EQ> rbh = rstar + mubh
COMMENT> Interests received by households on their government debt holdings
IDENTITY> intgh
EQ> intgh = rbh * TSLAG(bh,1)
COMMENT> Markup on loans to firms
BEHAVIORAL> mul
TSRANGE 1998 1 2021 1
EQ> mul = mul0 + mul1*TSLAG(mub,1)
COEFF> mul0 mul1
STORE> coe(2)
COMMENT> Net interest payments received by households
IDENTITY> inth
EQ> inth = intgh + intmh - intlh
COMMENT> Markup on personal loans to households
BEHAVIORAL> mulh
TSRANGE 1998 1 2021 1
EQ> mulh = mulh0 + mulh1*TSLAG(mub,1)
COEFF> mulh0 mulh1
STORE> coe(7)
COMMENT> Interest rate on loans to households
IDENTITY> rlh
EQ> rlh = rstar + mulh
COMMENT> Wage share (endogenous)
IDENTITY> Omega
EQ> Omega = wb/y
COMMENT> Other assets of households
BEHAVIORAL> oah
TSRANGE 1998 1 2021 1
EQ> oah = oah0 + lambda_oah*TSLAG(oah,1)
COEFF> oah0 lambda_oah
STORE> coe(18)
COMMENT> BANKING SECTOR --------------------------------------------------------
COMMENT> Total supply of loans
IDENTITY> ls
EQ> ls = lf + lh
COMMENT> Supply of bank deposits
IDENTITY> ms
EQ> ms = mh
COMMENT> Banks profit
IDENTITY> fb
EQ> fb = intb
COMMENT> Total interests payments received by banks
IDENTITY> intb
EQ> intb = intgb + intf + intlh - intmh
COMMENT> Net interest payments received by banks on government bills
IDENTITY> intgb
EQ> intgb = rbb*TSLAG(bb,1)
COMMENT> Stock of bills held by banks
BEHAVIORAL> Lbb
TSRANGE 1998 1 2021 1
EQ> Lbb = lambdabb1*TSLAG(log(ls+hbd+bb),1) + lambdabb2*dum
COEFF> lambdabb1 lambdabb2
STORE> coe(33)
COMMENT> bb
IDENTITY> bb
EQ> bb = exp(Lbb)
COMMENT> Total wealth accumulated by banks
IDENTITY> vb
EQ> vb = oab + hbd + bb + ls - ms
COMMENT> GOVERNMENT SECTOR -----------------------------------------------------
COMMENT> Tax revenue
BEHAVIORAL> tax
TSRANGE 1998 1 2021 1
EQ> tax = tau1*(TSLAG(wb,1)) + tau2*(TSLAG((yd - wb),1)) + tau3*(TSLAG(vh,1))
COEFF> tau1 tau2 tau3
STORE> coe(10)
COMMENT> Transfers and benefits
BEHAVIORAL> tr
TSRANGE 1998 1 2021 1
EQ> tr = tau4*TSLAG(tr,1) + tau5*TSDELTA(un,1)
COEFF> tau4 tau5
STORE> coe(11)
COMMENT> Government deficit
IDENTITY> def
EQ> def = gov + tr + intg - tax - fcb
COMMENT> Government debt stock
IDENTITY> deb
EQ> deb = bs
COMMENT> Interest payments on government debt
IDENTITY> intg
EQ> intg = rb*TSLAG(deb,1)
COMMENT> Supply of government bills and bonds
IDENTITY> bs
EQ> bs = TSLAG(bs,1) + def
COMMENT> Net wealth of goverment sector (Note: negative value)
IDENTITY> vg
EQ> vg = - bs + oag
COMMENT> PORTFOLIO EQUATIONS ---------------------------------------------------
COMMENT> Holdings of government bills (log)
BEHAVIORAL> Lbh
TSRANGE 1998 1 2021 1
EQ> Lbh = lambda20*TSLAG(log(vh),1) + lambda21*dum
COEFF> lambda20 lambda21
STORE> coe(16)
COMMENT> Holdings of shares (log)
BEHAVIORAL> Leh
TSRANGE 1998 1 2021 1
EQ> Leh = lambda10*TSLAG(log(vh),1)
COEFF> lambda10
STORE> coe(15)
COMMENT> Holding of shares
IDENTITY> eh
EQ> eh = exp(Leh)
COMMENT> Holding of government bills
IDENTITY> bh
EQ> bh = exp(Lbh)
COMMENT> Holdings of cash (log)
BEHAVIORAL> Lhh
TSRANGE 1998 1 2021 1
EQ> TSDELTA(Lhh,1) = lambdac*log(cons/pc)
COEFF> lambdac
STORE> coe(17)
COMMENT> Holding of cash
IDENTITY> hh
EQ> hh = exp(Lhh)
COMMENT> Holdings of deposits
IDENTITY> mh
EQ> mh = vh + lh - hh - bh - eh - oah
COMMENT> CENTRAL BANK ----------------------------------------------------------
COMMENT> CB holdings of government bills
IDENTITY> bcb
EQ> bcb = bs - bh - bb - brow
COMMENT> Supply of cash
IDENTITY> hs
EQ> hs = bcb + oacb - vcb
COMMENT> Profit realised and distributed by CB
IDENTITY> fcb
EQ> fcb = intg - intgh - intgb - introw
COMMENT> Reserve requirement: demand
IDENTITY> hbd
EQ> hbd = rho*ms
COMMENT> Reserve ratio
BEHAVIORAL> rho
TSRANGE 1998 1 2021 1
EQ> rho = rho_1*TSLAG(rho,1)
COEFF> rho_1
STORE> coe(56)
COMMENT> Total demand for cash and reserves (auxiliary)
IDENTITY> hd
EQ> hd = hbd + hh
COMMENT> FOREIGN SECTOR --------------------------------------------------------
COMMENT> Nominal import
IDENTITY> im
EQ> im = exp(LimR) * p / 100
COMMENT> Nominal export
IDENTITY> x
EQ> x = exp(LxR) * p / 100
COMMENT> Foreign income. Note: yf1 = (1 + gF)
BEHAVIORAL> yf
TSRANGE 1998 1 2021 1
EQ> yf = yf1*TSLAG(yf,1)
COEFF> yf1
STORE> coe(22)
COMMENT> Net export (trade balance)
IDENTITY> nx
EQ> nx = x - im
COMMENT> Stock of Italian bills debt held by foreign agents
IDENTITY> brow
EQ> brow = lambdarow*bs
COMMENT> Total wealth accumulated by RoW
IDENTITY> vrow
EQ> vrow = brow + oarow
COMMENT> Net interest payments received by RoW on government bills
IDENTITY> introw
EQ> introw = rbrow * TSLAG(brow,1)
COMMENT> Exchange rate: dollars per 1 euro
BEHAVIORAL> exr
TSRANGE 1998 1 2021 1
EQ> exr = exr1*MOVAVG(exr,2)
COEFF> exr1
STORE> coe(58)
COMMENT> Share of government bills purchased by foreign agents
BEHAVIORAL> lambdarow
TSRANGE 1998 1 2021 1
EQ> lambdarow = lambdarow1*TSLAG(lambdarow,1) + lambdarow2*TSLAG(rbrow,1)
COEFF> lambdarow1 lambdarow2
STORE> coe(31)
COMMENT> INTEREST RATES --------------------------------------------------------
COMMENT> Return rate on shares
IDENTITY> re
EQ> re = fdf/TSLAG(eh,1)
COMMENT> Policy rate
BEHAVIORAL> rstar
TSRANGE 1998 1 2021 1
EQ> rstar = r0
COEFF> r0
STORE> coe(25)
COMMENT> Average risk premium on government bond
IDENTITY> rb
EQ> rb = rstar + mub
COMMENT> Interest rate received by banks on their government debt holdings
IDENTITY> rbb
EQ> rbb = rstar + mubb
COMMENT> Interest rate received by RoW on their government debt holdings
IDENTITY> rbrow
EQ> rbrow = rstar + mubrow
COMMENT> Premium on government bills held by banks
BEHAVIORAL> mubb
TSRANGE 1998 1 2021 1
EQ> mubb = mubb1*TSLAG(mubb,1) + mubb2*mub
COEFF> mubb1 mubb2
STORE> coe(45)
COMMENT> Premium on government bills held by RoW
BEHAVIORAL> mubrow
TSRANGE 1998 1 2021 1
EQ> mubrow = mubrow1*TSLAG(mubrow,1) + mubrow2*mub
COEFF> mubrow1 mubrow2
STORE> coe(46)
COMMENT> Interests paid by banks to households on deposits and other A/L
BEHAVIORAL> intmh
TSRANGE 1998 1 2021 1
EQ> intmh = intmh0 + intmh1*mh
COEFF> intmh0 intmh1
STORE> coe(47)
COMMENT> LABOUR MARKET ---------------------------------------------------------
COMMENT> Wage bill
IDENTITY> wb
EQ> wb = w*nd
COMMENT> Labour productivity (real value added per employee)
BEHAVIORAL> prod
EQ> TSDELTALOG(prod,1) = nu0 + nu1 * TSDELTALOG(100*w/p,1) + nu2 * TSDELTALOG(100*y/p,2)
COEFF> nu0 nu1 nu2
STORE> coe(51)
COMMENT> Employment: demand for labour
IDENTITY> nd
EQ> nd = (100*y)/(prod*p)
COMMENT> Labour force (log)
BEHAVIORAL> Lns
TSRANGE 1998 1 2021 1
EQ> Lns = nu1*TSLAG(Lns,1) + nu2*( log(nd) -TSLAG(Lns,1))
COEFF> nu1 nu2
STORE> coe(27)
COMMENT> Labour force
IDENTITY> ns
EQ> ns = exp(Lns)
COMMENT> Wage rate growth
BEHAVIORAL> gw
TSRANGE 1998 1 2021 1
EQ> gw = omega1*TSDELTAP(p/100,1) + omega2*TSDELTA(un,1)
COEFF> omega1 omega2
STORE> coe(28)
COMMENT> Nominal wage rate
IDENTITY> w
EQ> w = TSLAG(w,1)*(1+gw)
COMMENT> Unemployment rate
IDENTITY> un
EQ> un = 1-(nd/ns)
COMMENT> PRODUCTION AND PRICES -------------------------------------------------
COMMENT> Price level (GDP deflator)
IDENTITY> p
EQ> p = exp(Lp)
COMMENT> Consumer price index
IDENTITY> pc
EQ> pc = exp(Lpc)
COMMENT> Log foreign price level --- exogenous
BEHAVIORAL> Lp_row
TSRANGE 1998 1 2021 1
EQ> Lp_row = prow0 + prow1*TSLAG(Lp_row,1)
COEFF> prow0 prow1
STORE> coe(60)
COMMENT> Foreign price level
IDENTITY> p_row
EQ> p_row = exp(Lp_row)
COMMENT> Price of import
IDENTITY> p_im
EQ> p_im = exp(Lp_im)
COMMENT> Inflation rate based on GDP deflator
IDENTITY> infl
EQ> infl = (p - TSLAG(p,1))/TSLAG(p,1)
COMMENT> Inflation rate based on CPI
IDENTITY> inflc
EQ> inflc = (pc - TSLAG(pc,1))/TSLAG(pc,1)
COMMENT> Deficit to GDP ratio
IDENTITY> def_ratio
EQ> def_ratio = def/y
COMMENT> Debt to GDP ratio
IDENTITY> deb_ratio
EQ> deb_ratio = deb/y
COMMENT> ENERGY IMPORT ---------------------------------------------------------
COMMENT> Energy Price level
IDENTITY> p_en
EQ> p_en = exp(Lp_en)
COMMENT> Share of energy products to total import
BEHAVIORAL> perc_en
TSRANGE 1998 1 2021 1
EQ> perc_en = enm1*infl_en + enm2*TSLAG(log(y/p),1)
COEFF> enm1 enm2
STORE> coe(54)
COMMENT> Import of energy products
IDENTITY> im_en
EQ> im_en = im * perc_en
COMMENT> Energy inflation rate. Note: high values, so do not use dlog
IDENTITY> infl_en
EQ> infl_en = (p_en - TSLAG(p_en,1))/TSLAG(p_en,1)
COMMENT> Log of energy price --- exogenous
BEHAVIORAL> Lp_en
TSRANGE 1998 1 2021 1
EQ> Lp_en = ep1*TSLAG(Lp_en,1)
COEFF> ep1
STORE> coe(53)
COMMENT> OTHER ACCOUNTING-CONSISTENCY EQUATIONS --------------------------------
COMMENT> Other payments or receipts received by firms
IDENTITY> opf
EQ> opf = vf - TSLAG(vf,1) - (cons + gov + nx - wb - intf - fdf)
COMMENT> Other payments or receipts received by banks
IDENTITY> opb
EQ> opb = fb - intb + (vb - tslag(vb,1))
COMMENT> Other payments or receipts by government
IDENTITY> opg
EQ> opg = vg - TSLAG(vg,1) - ( -gov + tax - tr - intg + fcb)
COMMENT> Other payments or receipts received by CB
IDENTITY> opcb
EQ> opcb = vcb - TSLAG(vcb,1)
COMMENT> Other payments or receipts received by RoW
IDENTITY> oprow
EQ> oprow = -(oph + opf + opg + opb + opcb)
COMMENT> Other payments or receipts of households
BEHAVIORAL> oph
TSRANGE 1998 1 2021 1
EQ> TSDELTAP(oph,1) = par_oph * TSDELTAP(oph,1)
COEFF> par_oph
STORE> coe(57)
COMMENT> Other financial assets held by RoW
IDENTITY> oarow
EQ> oarow = - (oah + oaf + oab + oacb + oag)
COMMENT> Total wealth accumulated by central bank
IDENTITY> vcb
EQ> vcb = -(vh + vf + vrow + vg + vb)
COMMENT> Other financial assets/liabilities of firms
BEHAVIORAL> oaf
TSRANGE 1998 1 2021 1
EQ> oaf = oaf0 + lambda_oaf*TSLAG(oaf,1)
COEFF> oaf0 lambda_oaf
STORE> coe(38)
COMMENT> Other financial assets/liabilities of government
BEHAVIORAL> oag
TSRANGE 1998 1 2021 1
EQ> oag = oag0 + lambda_oag*TSLAG(oag,1)
COEFF> oag0 lambda_oag
STORE> coe(44)
COMMENT> Other financial assets held by banks
BEHAVIORAL> oab
TSRANGE 1998 1 2021 1
EQ> oab = oab0 + lambda_oab*TSLAG(oab,1)
COEFF> oab0 lambda_oab
STORE> coe(52)
COMMENT> Other financial assets held by ECB
BEHAVIORAL> oacb
TSRANGE 1998 1 2021 1
EQ> oacb = oacb0 + lambda_oacb*TSLAG(oacb,1)
COEFF> oacb0 lambda_oacb
STORE> coe(55)
COMMENT> ADDITIONAL CALCULATIONS --------------------------------
COMMENT> Real GDP
IDENTITY> yR
EQ> yR = 100*y/p
COMMENT> Real investment including depreciation (note: iddR > idR)
IDENTITY> iddR
EQ> iddR = 100*id/p
COMMENT> Real export
IDENTITY> xR
EQ> xR = 100*x/p
COMMENT> Real investment including depreciation (note: different from idR)
IDENTITY> imR
EQ> imR = 100*im/p
COMMENT> KEY BEHAVIOURAL EQUATIONS --------------------------------
COMMENT> Real consumption (log). Note: yd replaced with y because the latter is more stable over time
BEHAVIORAL> LconsR
TSRANGE 1998 1 2021 1
EQ> LconsR = alpha1*TSLAG(log(y*100/pc),1) + alpha2*TSLAG( log(vh*100/pc),1)
COEFF> alpha1 alpha2
STORE> coe(5)
COMMENT> Government consumption
BEHAVIORAL> gov
TSRANGE 1998 1 2021 1
EQ> gov = sigma1*TSLAG((gov/p),1)*p
COEFF> sigma1
RESTRICT> sigma1 = 1.01
STORE> coe(12)
COMMENT> Real investment net of capital depreciation
BEHAVIORAL> LidR
TSRANGE 1998 1 2021 1
EQ> LidR = gamma0 + gamma1*TSLAG(log(y)/log(k),1)
COEFF> gamma0 gamma1
STORE> coe(1)
COMMENT> Log of real export
BEHAVIORAL> LxR
TSRANGE 1998 1 2021 1
EQ> LxR = x0 + x1*TSLAG(log(yf),1) + x2*TSLAG(exr*p/p_row,1)
COEFF> x0 x1 x2
STORE> coe(21)
COMMENT> Log of real import
BEHAVIORAL> LimR
TSRANGE 1998 1 2021 1
EQ> LimR = m0 + m1*TSLAG(log(y),1) + m2*TSLAG(p_im/p,1)
COEFF> m0 m1 m2
STORE> coe(20)
COMMENT> Log of price of import
BEHAVIORAL> Lp_im
TSRANGE 1998 1 2021 1
EQ> Lp_im = pim0 + pim1*TSLAG(exr,1) + pim2*TSLAG(Lp_row,1)
COEFF> pim0 pim1 pim2
STORE> coe(59)
COMMENT> Log of price level (GDP deflator)
BEHAVIORAL> Lp
TSRANGE 1998 1 2021 1
EQ> Lp = viy1*TSLAG(Lp_en,1) + viy2*TSLAG(Lp_row,1) + viy3*TSLAG(log(100*y/p),1)
COEFF> viy1 viy2 viy3
STORE> coe(30)
COMMENT> Log of consumer price index
BEHAVIORAL> Lpc
TSRANGE 1998 1 2021 1
EQ> Lpc = vic1*TSLAG(Lp_en,1) + vic2*TSLAG(Lp_row,1) + vic3*TSLAG(log(100*y/p),1)
COEFF> vic1 vic2 vic3
STORE> coe(30)
COMMENT> Average premium on government bills
BEHAVIORAL> mub
TSRANGE 1998 1 2021 1
EQ> mub = mub2*TSLAG(deb/y,1) + mub3*bcb/bs + mub4*rstar
COEFF> mub2 mub3 mub4
STORE> coe(39)
END"
Notice that the two price equations have been defined including real GDP among the deflators. This choice is due to four reasons:
-
Income effect. Real GDP can be considered a proxy for the overall volume of activity or income in an economy. Changes in income can affect the demand for goods and services, thus indirectly affecting the price level.
-
Aggregate demand effect. Real GDP reflects the aggregate demand. When aggregate demand increases, it can put direct upward pressure on prices, particularly when supply is constrained (as it happened in recent years). Therefore, including real GDP in the price equation allows capturing this demand-pressure effect.
-
Macroeconomic and labour market conditions. Real GDP can be taken as a key indicator of the overall health of the economy, hence labour market conditions. A higher employment rate and a lower unemployment rate are usually associated with higher nominal wages. Real GDP serves as a summary measure of these macroeconomic and labour market conditions.
-
Medium-term trend. Real GDP can also be used to capture medium-term trend in the economy, which can in turn influence the price level.
An alternative specification of these equations, including the unit labour cost among the regressors (instead of real GDP), could be:
COMMENT> Log of price level (GDP deflator)
BEHAVIORAL> Lp
TSRANGE 1998 1 2021 1
EQ> TSDELTA(Lp,1) = viy1*TSDELTA(Lp_en,1) + viy2*TSDELTA(Lp_row,1) + viy3*TSDELTA(log(w),1) + viy4*TSDELTA(log(prod),1)
COEFF> viy1 viy2 viy3 viy4
STORE> coe(30)
COMMENT> Log of consumer price index
BEHAVIORAL> Lpc
TSRANGE 1998 1 2021 1
EQ> TSDELTA(Lpc,1) = vic1*TSDELTA(Lp_en,1) + vic2*TSDELTA(Lp_row,1) + vic3*TSDELTA(log(w),1) + vic4*TSDELTA(log(prod),1)
COEFF> vic1 vic2 vic3 vic4
STORE> coe(30)While our qualitative results would not be affected, and the coefficients exhibit the correct signs, the latter are barely significant. This may be attributed to the specific situation of the Italian labour market, where workers have lost most of their bargaining power, while the goods market is characterised by an oligopolistic structure. This is why we pragmatically opted for real GDP in the final specification of the model.
Having clarified that, the fourth step is to load the model.
#Load the model
S_model=LOAD_MODEL(modelText = S_model.txt)This allows displaying the structure of the model (including the number of behavioural equations, identities, and coefficients) in the Console.
Analyzing behaviorals...
Analyzing identities...
Optimizing...
Loaded model "S_model.txt":
40 behaviorals
81 identities
77 coefficients
...LOAD MODEL OKThe fifth step is to associate the model with the imported data. Note: a time series is required for each variable defined in the model, including dummies.
#Attribute values to model variables and coefficients
S_modelData=list(
pc = TIMESERIES(c(DataEE$Pc),
START=c(1995,1),FREQ=1),
Lpc = TIMESERIES(c(log(DataEE$Pc)),
START=c(1995,1),FREQ=1),
gid = TIMESERIES(c(DataEE$gid),
START=c(1995,1),FREQ=1),
gidR = TIMESERIES(c(DataEE$gid-DataEE$PI),
START=c(1995,1),FREQ=1),
infl = TIMESERIES(c(DataEE$PI),
START=c(1995,1),FREQ=1),
inflc = TIMESERIES(c(DataEE$CPI),
START=c(1995,1),FREQ=1),
Lp = TIMESERIES(c(log(DataEE$Py)),
START=c(1995,1),FREQ=1),
p_en = TIMESERIES(c(DataEE$Pen2 ),
START=c(1995,1),FREQ=1),
Lp_en = TIMESERIES(c(log(DataEE$Pen2)),
START=c(1995,1),FREQ=1),
infl_en = TIMESERIES(c(DataEE$PIen),
START=c(1995,1),FREQ=1),
im_en = TIMESERIES(c(DataEE$IMen),
START=c(1995,1),FREQ=1),
perc_en = TIMESERIES(c(DataEE$IMen/DataEE$IM),
START=c(1995,1),FREQ=1),
Lim_en = TIMESERIES(c(log(DataEE$IMen)),
START=c(1995,1),FREQ=1),
y = TIMESERIES(c(DataEE$Y),
START=c(1995,1),FREQ=1),
gy = TIMESERIES(c(DataEE$gy),
START=c(1995,1),FREQ=1),
cons = TIMESERIES(c(DataEE$CONS),
START=c(1995,1),FREQ=1),
id = TIMESERIES(c(DataEE$INV),
START=c(1995,1),FREQ=1),
gov = TIMESERIES(c(DataEE$GOV),
START=c(1995,1),FREQ=1),
x = TIMESERIES(c(DataEE$X),
START=c(1995,1),FREQ=1),
im = TIMESERIES(c(DataEE$IM),
START=c(1995,1),FREQ=1),
Lx = TIMESERIES(c(log(DataEE$X)),
START=c(1995,1),FREQ=1),
Lim = TIMESERIES(c(log(DataEE$IM)),
START=c(1995,1),FREQ=1),
LxR = TIMESERIES(c(log(100*DataEE$X/DataEE$Py)),
START=c(1995,1),FREQ=1),
LimR = TIMESERIES(c(log(100*DataEE$IM/DataEE$Py)),
START=c(1995,1),FREQ=1),
consR = TIMESERIES(c(DataEE$CONS*100/DataEE$Py),
START=c(1995,1),FREQ=1),
LconsR = TIMESERIES(c(log(DataEE$CONS*100/DataEE$Py)),
START=c(1995,1),FREQ=1),
idR = TIMESERIES(c(DataEE$INVnet*100/DataEE$Py),
START=c(1995,1),FREQ=1),
LidR = TIMESERIES(c(log(DataEE$INVnet*100/DataEE$Py)),
START=c(1995,1),FREQ=1),
nx = TIMESERIES(c(DataEE$X-DataEE$IM),
START=c(1995,1),FREQ=1),
wb = TIMESERIES(c(DataEE$WB),
START=c(1995,1),FREQ=1),
yd = TIMESERIES(c(DataEE$YD),
START=c(1995,1),FREQ=1),
vh = TIMESERIES(c(DataEE$NVh),
START=c(1995,1),FREQ=1),
k = TIMESERIES(c(DataEE$K),
START=c(1995,1),FREQ=1),
deltak = TIMESERIES(c(DataEE$Delta ),
START=c(1995,1),FREQ=1),
intf = TIMESERIES(c(DataEE$INTf),
START=c(1995,1),FREQ=1),
lf = TIMESERIES(c(-DataEE$Lf),
START=c(1995,1),FREQ=1),
fdf = TIMESERIES(c(DataEE$DIV),
START=c(1995,1),FREQ=1),
ff = TIMESERIES(c(DataEE$Ff),
START=c(1995,1),FREQ=1),
fuf = TIMESERIES(c(DataEE$FUf),
START=c(1995,1),FREQ=1),
es = TIMESERIES(c(-DataEE$Es),
START=c(1995,1),FREQ=1),
eh = TIMESERIES(c(DataEE$Eh),
START=c(1995,1),FREQ=1),
Leh = TIMESERIES(c(log(DataEE$Eh)),
START=c(1995,1),FREQ=1),
tax = TIMESERIES(c(DataEE$TAX),
START=c(1995,1),FREQ=1),
tr = TIMESERIES(c(DataEE$TR),
START=c(1995,1),FREQ=1),
Ltax = TIMESERIES(c(log(DataEE$TAX)),
START=c(1995,1),FREQ=1),
Ltr = TIMESERIES(c(log(DataEE$TR)),
START=c(1995,1),FREQ=1),
lh = TIMESERIES(c(-DataEE$Lh),
START=c(1995,1),FREQ=1),
ls = TIMESERIES(c(DataEE$Ls),
START=c(1995,1),FREQ=1),
mh = TIMESERIES(c(DataEE$Mh),
START=c(1995,1),FREQ=1),
ms = TIMESERIES(c(-DataEE$Ms),
START=c(1995,1),FREQ=1),
inth = TIMESERIES(c(DataEE$INTh),
START=c(1995,1),FREQ=1),
un = TIMESERIES(c( (DataEE$Ns-DataEE$Nd)/DataEE$Ns ),
START=c(1995,1),FREQ=1),
Omega = TIMESERIES(c(DataEE$WB/DataEE$Y),
START=c(1995,1),FREQ=1),
ns = TIMESERIES(c(DataEE$Ns),
START=c(1995,1),FREQ=1),
Lns = TIMESERIES(c(log(DataEE$Ns)),
START=c(1995,1),FREQ=1),
bs = TIMESERIES(c(-DataEE$Bs),
START=c(1995,1),FREQ=1),
bh = TIMESERIES(c(DataEE$Bh),
START=c(1995,1),FREQ=1),
Lbh = TIMESERIES(c(log(DataEE$Bh)),
START=c(1995,1),FREQ=1),
rbb = TIMESERIES(c(DataEE$Rbb ),
START=c(1995,1),FREQ=1),
mubb = TIMESERIES(c(DataEE$Rbb-DataEE$Rstar),
START=c(1995,1),FREQ=1),
rbrow = TIMESERIES(c(DataEE$Rbrow ),
START=c(1995,1),FREQ=1),
mubrow = TIMESERIES(c(DataEE$Rbrow-DataEE$Rstar),
START=c(1995,1),FREQ=1),
rbh = TIMESERIES(c(DataEE$Rbh ),
START=c(1995,1),FREQ=1),
mubh = TIMESERIES(c(DataEE$Rbh-DataEE$Rstar),
START=c(1995,1),FREQ=1),
introw = TIMESERIES(c(DataEE$INTrow ),
START=c(1995,1),FREQ=1),
fcb = TIMESERIES(c(DataEE$Fcb),
START=c(1995,1),FREQ=1),
re = TIMESERIES(c(DataEE$Re),
START=c(1995,1),FREQ=1),
hh = TIMESERIES(c(DataEE$Hh),
START=c(1995,1),FREQ=1),
Lhh = TIMESERIES(c(log(DataEE$Hh)),
START=c(1995,1),FREQ=1),
rho = TIMESERIES(c(DataEE$RHO),
START=c(1995,1),FREQ=1),
yf = TIMESERIES(c(DataEE$Yrow/1000),
START=c(1995,1),FREQ=1),
rstar = TIMESERIES(c(DataEE$Rstar),
START=c(1995,1),FREQ=1),
mub = TIMESERIES(c(DataEE$Rb-DataEE$Rstar),
START=c(1995,1),FREQ=1),
deb = TIMESERIES(c(DataEE$Deb),
START=c(1995,1),FREQ=1),
vg = TIMESERIES(c(DataEE$Vg),
START=c(1995,1),FREQ=1),
def = TIMESERIES(c(DataEE$DEF1),
START=c(1995,1),FREQ=1),
nd = TIMESERIES(c(DataEE$Nd),
START=c(1995,1),FREQ=1),
ndstar = TIMESERIES(c(DataEE$Y/DataEE$Prod),
START=c(1995,1),FREQ=1),
w = TIMESERIES(c(DataEE$w),
START=c(1995,1),FREQ=1),
gw = TIMESERIES(c(DataEE$gw),
START=c(1995,1),FREQ=1),
bb = TIMESERIES(c(DataEE$Bb),
START=c(1995,1),FREQ=1),
Lbb = TIMESERIES(c(log(DataEE$Bb)),
START=c(1995,1),FREQ=1),
bcb = TIMESERIES(c(DataEE$Bcb),
START=c(1995,1),FREQ=1),
bb_not = TIMESERIES(c(-DataEE$Ms - DataEE$Ls - DataEE$Hbd),
START=c(1995,1),FREQ=1),
hbd = TIMESERIES(c(DataEE$Hbd),
START=c(1995,1),FREQ=1),
hs = TIMESERIES(c(-DataEE$Hs ),
START=c(1995,1),FREQ=1),
hd = TIMESERIES(c(-DataEE$Hs),
START=c(1995,1),FREQ=1),
fb = TIMESERIES(c(DataEE$Fb ),
START=c(1995,1),FREQ=1),
lambdacb = TIMESERIES(c(-DataEE$Bcb/DataEE$Bs),
START=c(1995,1),FREQ=1),
lambdarow = TIMESERIES(c(-DataEE$Brow/DataEE$Bs),
START=c(1995,1),FREQ=1),
oph = TIMESERIES(c(DataEE$OPh),
START=c(1995,1),FREQ=1),
opb = TIMESERIES(c(DataEE$OPb),
START=c(1995,1),FREQ=1),
opcb = TIMESERIES(c(DataEE$OPcb),
START=c(1995,1),FREQ=1),
opf = TIMESERIES(c(DataEE$OPf),
START=c(1995,1),FREQ=1),
opg = TIMESERIES(c(DataEE$OPg),
START=c(1995,1),FREQ=1),
vf = TIMESERIES(c(DataEE$Vf),
START=c(1995,1),FREQ=1),
oprow = TIMESERIES(c(DataEE$OProw),
START=c(1995,1),FREQ=1),
vb = TIMESERIES(c(DataEE$Vb),
START=c(1995,1),FREQ=1),
vrow = TIMESERIES(c(DataEE$Vrow),
START=c(1995,1),FREQ=1),
oah = TIMESERIES(c(DataEE$OAh),
START=c(1995,1),FREQ=1),
Loah = TIMESERIES(c(log(DataEE$OAh)),
START=c(1995,1),FREQ=1),
oaf = TIMESERIES(c(DataEE$OAf),
START=c(1995,1),FREQ=1),
oab = TIMESERIES(c(DataEE$OAb),
START=c(1995,1),FREQ=1),
oag = TIMESERIES(c(DataEE$OAg),
START=c(1995,1),FREQ=1),
oacb = TIMESERIES(c(DataEE$OAcb),
START=c(1995,1),FREQ=1),
oarow = TIMESERIES(c(DataEE$OArow),
START=c(1995,1),FREQ=1),
vcb = TIMESERIES(c(DataEE$Vcb),
START=c(1995,1),FREQ=1),
p = TIMESERIES(c(DataEE$Py),
START=c(1995,1),FREQ=1),
prod = TIMESERIES(c(DataEE$ProdR),
START=c(1995,1),FREQ=1),
rl = TIMESERIES(c(DataEE$Rl ),
START=c(1995,1),FREQ=1),
mul = TIMESERIES(c(DataEE$Rl - DataEE$Rstar ),
START=c(1995,1),FREQ=1),
intgb = TIMESERIES(c(DataEE$INTgb),
START=c(1995,1),FREQ=1),
intgh = TIMESERIES(c(DataEE$INTgh ),
START=c(1995,1),FREQ=1),
intb = TIMESERIES(c(DataEE$INTb),
START=c(1995,1),FREQ=1),
intmh = TIMESERIES(c(DataEE$INTm ),
START=c(1995,1),FREQ=1),
intlh = TIMESERIES(c(DataEE$INTlh ),
START=c(1995,1),FREQ=1),
rlh = TIMESERIES(c(DataEE$Rlh ),
START=c(1995,1),FREQ=1),
mulh = TIMESERIES(c(DataEE$Rlh - DataEE$Rstar ),
START=c(1995,1),FREQ=1),
rb = TIMESERIES(c(DataEE$Rb),
START=c(1995,1),FREQ=1),
mub = TIMESERIES(c(DataEE$Rb-DataEE$Rstar),
START=c(1995,1),FREQ=1),
intg = TIMESERIES(c(DataEE$INTg),
START=c(1995,1),FREQ=1),
brow = TIMESERIES(c(DataEE$Brow),
START=c(1995,1),FREQ=1),
pc = TIMESERIES(c(DataEE$Pc),
START=c(1995,1),FREQ=1),
exr = TIMESERIES(c(DataEE$Exr),
START=c(1995,1),FREQ=1),
exr42 = TIMESERIES(c(DataEE$Exr42 ),
START=c(1995,1),FREQ=1),
exr42 = TIMESERIES(c(DataEE$Exr42 ),
START=c(1995,1),FREQ=1),
dum = TIMESERIES(c(0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1),
START=c(1995,1),FREQ=1),
p_im = TIMESERIES(c(DataEE$Pim ),
START=c(1995,1),FREQ=1),
Lp_im = TIMESERIES(c(log(DataEE$Pim)),
START=c(1995,1),FREQ=1),
p_im_en = TIMESERIES(c(DataEE$Pim_en ),
START=c(1995,1),FREQ=1),
Lp_im_en = TIMESERIES(c(log(DataEE$Pim_en)),
START=c(1995,1),FREQ=1),
p_row = TIMESERIES(c(DataEE$Py_row ),
START=c(1995,1),FREQ=1),
Lp_row = TIMESERIES(c(log(DataEE$Py_row)),
START=c(1995,1),FREQ=1),
yR = TIMESERIES(c(DataEE$Y*100/DataEE$Py),
START=c(1995,1),FREQ=1),
iddR = TIMESERIES(c(DataEE$INV*100/DataEE$Py),
START=c(1995,1),FREQ=1),
xR = TIMESERIES(c(DataEE$X*100/DataEE$Py),
START=c(1995,1),FREQ=1),
imR = TIMESERIES(c(DataEE$IM*100/DataEE$Py),
START=c(1995,1),FREQ=1),
def_ratio = TIMESERIES(c(DataEE$DEF1/DataEE$Y),
START=c(1995,1),FREQ=1),
deb_ratio = TIMESERIES(c(DataEE$Deb/DataEE$Y),
START=c(1995,1),FREQ=1)
)
#Load the data into the model
S_model=LOAD_MODEL_DATA(S_model,S_modelData)The sixth step is to estimate model coefficients:
#Estimate model coefficients
S_model=ESTIMATE(S_model
,TSRANGE = c(1998,1,2019,1) #Choose time range for estimations
,forceTSRANGE = TRUE #If TRUE, the TSRANGE above takes precedence over individual equations TSRANGEs
,CHOWTEST = FALSE #If TRUE, performs Chow test: stability analysis (reject H0 of "no structural break")
,CHOWPAR = NULL #If NULL, use last periods
)Now, we can execute the entire code, enabling the creation of the model and the estimation of the associated coefficients. Information on the estimations is displayed in the Console. For instance, the following details pertain to the estimation of the risk premium for government securities (
BEHAVIORAL EQUATION: mub
Estimation Technique: OLS
mub = 0.03222813 TSLAG(deb/y,1)
T-stat. 12.05956 ***
- 0.07942629 bcb/bs
T-stat. -3.732844 **
- 0.4223384 rstar
T-stat. -6.374726 ***
STATs:
R-Squared : 0.9773436
Adjusted R-Squared : 0.9737663
Durbin-Watson Statistic : 0.9611077
Sum of squares of residuals : 0.0002797596
Standard Error of Regression : 0.003837208
Log of the Likelihood Function : 92.7822
F-statistic : 273.2053
F-probability : 8.881784e-16
Akaike's IC : -177.5644
Schwarz's IC : -173.2002
Mean of Dependent Variable : 0.02246469
Number of Observations : 22
Number of Degrees of Freedom : 19
Current Sample (year-period) : 1998-1 / 2019-1
Signif. codes: *** 0.001 ** 0.01 * 0.05
...ESTIMATE OKThe details of the other estimations can be visualised by scrolling up through the Console information. The complete list of estimated coefficients is provided below:
| Name | Description | Value |
|---|---|---|
| Depreciation rate (average 1996-2019) | 0.046 | |
| Share of undistributed profits | 0.265 | |
| Elasticity of personal loans to consumption | 0.058 | |
| Premium on gov. bills held by households: coefficient 1 | 0.793 | |
| Premium on gov. bills held by households: coefficient 2 | 0.804 | |
| Markup on loans to firms: coefficient 1 | -0.014 | |
| Markup on loans to firms: coefficient 2 | 0.49 | |
| Markup on personal loans: coefficient 1 | 0.029 | |
| Markup on personal loans: coefficient 2 | 0.23 | |
| Other financial assets of households: coefficient 1 | 134828.967 | |
| Other financial assets of households: coefficient 2 | 0.908 | |
| Stock of bills held by banks: coefficient 1 | 0.918 | |
| Average tax rate on labour incomes | 0.514 | |
| Average tax rate on non-labour incomes | 0.061 | |
| Average tax rate on wealth | 0.042 | |
| Transfers and benefits: auto-regressive component | 1.043 | |
| Transfers and benefits: elasticity to unemployment rate | 374169.858 | |
| Holdings of government bills: coefficient 1 | 0.903 | |
| Holdings of shares as a ratio to total wealth | 0.925 | |
| Elasticity of cash holdings to real consumption | 0.006 | |
| Reserve ratio | 1.004 | |
| Foreign growth rate | 0.037 | |
| Exchange rate coefficient | 1 | |
| Policy rate | 0.019 | |
| Premium on government bills held by banks: coefficient 1 | 0.924 | |
| Premium on government bills held by banks: coefficient 2 | 0.248 | |
| Premium on government bills held by RoW: coefficient 1 | 0.554 | |
| Premium on government bills held by RoW: coefficient 2 | 0.916 | |
| Labour productivity: autonomous component | -0.004 | |
| Labour productivity: elasticity to real wage rate | 0.397 | |
| Labour productivity: elasticity to real output | 0.183 | |
| Labour force: auto-regressive component | 1.001 | |
| Labour force: elasticity to labour demand gap | 0.031 | |
| Wage growth rate: elasticity to inflation | 0.009 | |
| Wage growth rate: elasticity to unemployment rate | -0.786 | |
| Foreign price level: coefficient 1 | 0.207 | |
| Foreign price level: coefficient 2 | 0.959 | |
| Share of energy prod. to tot. import: elasticity to energy inflation | -0.002 | |
| Share of energy prod. to tot. import: elasticity to real output | 0.013 | |
| Energy price coefficient | 1.006 | |
| Other financial assets/liabilities of firms: coefficient 1 | 16702.341 | |
| Other financial assets/liabilities of firms: coefficient 2 | 0.897 | |
| Other financial assets/liabilities of government: coefficient 1 | 86022.616 | |
| Other financial assets/liabilities of government: coefficient 2 | 0.583 | |
| Other financial assets held by banks: coefficient 1 | -431517.076 | |
| Other financial assets held by banks: coefficient 2 | 0.745 | |
| Other financial assets held by ECB: coefficient 1 | -4533.844 | |
| Other financial assets held by ECB: coefficient 2 | 1.141 | |
| Marginal propensity to consume out of real income | 0.906 | |
| Marginal propensity to consume out of real wealth | 0.055 | |
| Real government spending: auto-regressive coefficient | 1.01 | |
| Real net investment: autonomous component | -117.512 | |
| Real net investment: elasticity to output to capital ratio | 138.616 | |
| Real export: autonomous component | 7.879 | |
| Real export: elasticity to foreign income | 0.512 | |
| Real export: elasticity to relative price of export | 0.08 | |
| Real import: autonomous component | 4.092 | |
| Real import: elasticity to domestic income | 0.633 | |
| Real import: elasticity to relative price of import | -0.106 | |
| GDP deflator: elasticity to energy price level | 0.058 | |
| GDP deflator: elasticity to foreign price level | 0.619 | |
| GDP deflator: elasticity to real output | 0.104 | |
| Consumer price index: elasticity to energy price level | 0.182 | |
| Consumer price index: elasticity to foreign price level | 0.505 | |
| Consumer price index: elasticity to real output | 0.101 | |
| Av. premium on gov. bills: elasticity to debt to GDP ratio | 0.032 | |
| Av. premium on gov. bills: elasticity to ECB’s holdings | -0.079 | |
| Av. premium on gov. bills: elasticity to policy rate | -0.422 |
Note: Simple OLS estimations have been employed. Additionally, log levels (instead of first differences) have been considered. In principle, this may raise concerns, as most variables are non-stationary, thus possibly leading to spurious correlations. The rationale for our choice is that observed annual time series are quite short and affected by structural breaks (such as the launch of the euro, the COVID-19 crisis, etc.). This makes the use of more sophisticated estimation techniques challenging. Furthermore, while the stationarity issue could be addressed by taking first differences, abandoning levels would imply a further loss of information. Lastly, note that the aim of the model is not to outpredict other methods, but to provide a theoretical tool to develop and assess alternative policy scenarios.
As mentioned earlier, the first step in defining the level of aggregation for the model and reclassifying available data is to create the balance sheet and the transactions-flow matrix of the economy. This process can also be used to double-check ex-post model consistency. The following code chunk facilitates the creation of the balance sheet using observed series (in both HTML and LaTeX format):
#Balance-sheet for Italy SFC model
#Observed series
################################################################################
#Choose a year (26=2020)
yr = 27
#Create row names for BS matrix
rownames<-c( "Cash and reserves",
"Deposits",
"Securities",
"Loans",
"Shares",
"Other net FA",
"Net financial wealth",
"Column total")
################################################################################
#Create firms aggregates
Firms <-c( 0,
0,
0,
round(-S_modelData$lf[yr], digits = 0),
round(-S_modelData$es[yr], digits = 0),
round(S_modelData$oaf[yr], digits = 0),
round(S_modelData$vf[yr], digits = 0),
round(-S_modelData$lf[yr]-S_modelData$es[yr]+S_modelData$oaf[yr]-S_modelData$vf[yr], digits = 0)
)
#Create table of results
FirmDataBS<-as.data.frame(Firms,row.names=rownames)
#Print firms column
kable(FirmDataBS)
################################################################################
#Create banks aggregates
Banks <-c( round(S_modelData$hbd[yr], digits = 0),
-round(S_modelData$ms[yr], digits = 0),
round(S_modelData$bb[yr], digits = 0),
round(S_modelData$ls[yr], digits = 0),
0,
round(S_modelData$oab[yr], digits = 0),
round(S_modelData$vb[yr], digits = 0),
round(S_modelData$hbd[yr]-S_modelData$ms[yr]+S_modelData$bb[yr]+S_modelData$ls[yr]+S_modelData$oab[yr]-S_modelData$vb[yr], digits = 0)
)
#Create table of results
BankDataBS<-as.data.frame(Banks,row.names=rownames)
#Print banks column
kable(BankDataBS)
################################################################################
#Create ECB aggregates
ECB <-c( -round(S_modelData$hs[yr], digits = 0),
0,
round(S_modelData$bcb[yr], digits = 0),
0,
0,
round(S_modelData$oacb[yr], digits = 0),
round(S_modelData$vcb[yr], digits = 0),
round(-S_modelData$hs[yr]+S_modelData$bcb[yr]+S_modelData$oacb[yr]-S_modelData$vcb[yr], digits = 0)
)
#Create table of results
ECBDataBS<-as.data.frame(ECB,row.names=rownames)
#Print ECB column
kable(ECBDataBS)
################################################################################
#Create government aggregates
Government <-c(0,
0,
round(-S_modelData$bs[yr], digits = 0),
0,
0,
round(S_modelData$oag[yr], digits = 0),
round(S_modelData$vg[yr], digits = 0),
round(-S_modelData$bs[yr]+S_modelData$oag[yr]-S_modelData$vg[yr], digits = 0)
)
#Create table of results
GovDataBS<-as.data.frame(Government,row.names=rownames)
#Print government column
kable(GovDataBS)
################################################################################
#Create household aggregates
Households <-c(round(S_modelData$hh[yr], digits = 0),
round(S_modelData$mh[yr], digits = 0),
round(S_modelData$bh[yr], digits = 0),
round(-S_modelData$lh[yr], digits = 0),
round(S_modelData$eh[yr], digits = 0),
round(S_modelData$oah[yr], digits = 0),
round(S_modelData$vh[yr], digits = 0),
round(S_modelData$hh[yr]+S_modelData$mh[yr]+S_modelData$bh[yr]-S_modelData$lh[yr]+S_modelData$eh[yr]+S_modelData$oah[yr]-S_modelData$vh[yr], digits = 0)
)
#Create table of results
HouseDataBS<-as.data.frame(Households,row.names=rownames)
#Print households column
kable(HouseDataBS)
################################################################################
#Create foreign sector aggregates
Foreign <-c( 0,
0,
round(S_modelData$brow[yr], digits = 0),
0,
0,
round(S_modelData$oarow[yr], digits = 0),
round(S_modelData$vrow[yr], digits = 0),
round(S_modelData$brow[yr]+S_modelData$oarow[yr]-S_modelData$vrow[yr], digits = 0)
)
#Create table of results
ROWDataBS<-as.data.frame(Foreign,row.names=rownames)
#Print foreign sector column
kable(ROWDataBS)
################################################################################
#Create row total (when entries > 2)
Total <-c( round(S_modelData$hh[yr]+S_modelData$hbd[yr]-S_modelData$hs[yr], digits = 0),
round(S_modelData$mh[yr]-S_modelData$ms[yr], digits = 0),
round(S_modelData$bh[yr]+S_modelData$bb[yr]+S_modelData$bcb[yr]+S_modelData$brow[yr]-S_modelData$bs[yr], digits = 0),
round(-S_modelData$lf[yr]-S_modelData$lh[yr]+S_modelData$ls[yr], digits = 0),
round(S_modelData$eh[yr]-S_modelData$es[yr], digits = 0),
round(S_modelData$oaf[yr]+S_modelData$oab[yr]+S_modelData$oacb[yr]+S_modelData$oag[yr]+S_modelData$oah[yr]+S_modelData$oarow[yr], digits = 0),
round(-(S_modelData$vf[yr]+S_modelData$vb[yr]+S_modelData$vcb[yr]+S_modelData$vg[yr]+S_modelData$vh[yr]+S_modelData$vrow[yr]), digits = 0),
round(S_modelData$hh[yr]+S_modelData$hbd[yr]-S_modelData$hs[yr] +
S_modelData$mh[yr]-S_modelData$ms[yr] +
S_modelData$bh[yr]+S_modelData$bb[yr]+S_modelData$bcb[yr]+S_modelData$brow[yr]-S_modelData$bs[yr] +
-S_modelData$lf[yr]-S_modelData$lh[yr]+S_modelData$ls[yr] +
S_modelData$eh[yr]-S_modelData$es[yr]+
S_modelData$oaf[yr]+S_modelData$oab[yr]+S_modelData$oacb[yr]+S_modelData$oag[yr]+S_modelData$oah[yr]+S_modelData$oarow[yr], digits = 0) )
#Create table of results
TotalDataBS<-as.data.frame(Total,row.names=rownames)
#Print foreign sector column
kable(TotalDataBS)
################################################################################
#Create BS matrix
Italy_BS_Matrix<-cbind(HouseDataBS,FirmDataBS,GovDataBS,BankDataBS,ECBDataBS,ROWDataBS,TotalDataBS)
kable(Italy_BS_Matrix)
################################################################################
#Upload libraries
library(knitr)
library(kableExtra)
#Create caption
captionBS <- paste("Table 1. Balance sheet in period", yr+1994)
#Create html table for BS
Italy_BS_Matrix %>%
kbl(caption=captionBS,
format= "html",
#format= "latex",
col.names = c("Households","Firms","Government","Banks","ECB","Foreign","Total"),
align="r") %>%
kable_classic(full_width = F, html_font = "helvetica")Similarly, the code chunk for the transactions-flow matrix is:
#TFM matrix for Italy SFC model
#Observed series
################################################################################
#Choose a year (26=2020)
yr=27
#Create row names for TFM matrix
rownames<-c( "Consumption",
"Total investment",
"Government spending",
"Export",
"Import",
"[GDP]",
"Taxes",
"Transfers",
"Wages",
"Interest payments",
"Corporate profit",
"Bank profit",
"CB seigniorage",
"Other payments",
"Change in cash and reserves",
"Change in deposits",
"Change in securities",
"Change in loans",
"Change in shares",
"Change in other net FA",
"Change in net wealth",
"Column total")
################################################################################
#Create firms (current) aggregates
Firms_c <-c( round(S_modelData$cons[yr], digits = 0),
round(S_modelData$id[yr], digits = 0),
round(S_modelData$gov[yr], digits = 0),
round(S_modelData$x[yr], digits = 0),
round(-S_modelData$im[yr], digits = 0),
paste("[",round(S_modelData$cons[yr]+S_modelData$id[yr]+S_modelData$gov[yr]+S_modelData$x[yr]-S_modelData$im[yr], digits = 0),"]"),
0,
0,
round(-S_modelData$wb[yr], digits = 0),
round(-S_modelData$intf[yr], digits = 0),
round(-S_modelData$ff[yr], digits = 0),
0,
0,
round(S_modelData$opf[yr], digits = 0),
0,
0,
0,
0,
0,
0,
0,
paste(round(S_modelData$y[yr]-S_modelData$wb[yr]-S_modelData$intf[yr]-S_modelData$ff[yr]+S_modelData$opf[yr] , digits = 0)))
#Create table of results
FirmData_c<-as.data.frame(Firms_c,row.names=rownames)
#Print firms column
kable(FirmData_c)
################################################################################
#Create firms (capital) aggregates
Firms_k <-c( 0,
round(-S_modelData$id[yr], digits = 0),
0,
0,
0,
0,
0,
0,
0,
0,
round(S_modelData$fu[yr], digits = 0),
0,
0,
0,
0,
0,
0,
round(S_modelData$lf[yr-1]-S_modelData$lf[yr], digits = 0),
round(S_modelData$es[yr-1]-S_modelData$es[yr], digits = 0),
round(-(S_modelData$oaf[yr-1]-S_modelData$oaf[yr]), digits = 0),
round(S_modelData$vf[yr]-S_modelData$vf[yr-1], digits = 0),
round(-S_modelData$id[yr] + S_modelData$fu[yr]-
-(S_modelData$vf[yr-1]-S_modelData$vf[yr]), digits = 0)
)
#Create table of results
FirmData_k<-as.data.frame(Firms_k,row.names=rownames)
#Print firms column
kable(FirmData_k)
################################################################################
#Create banks aggregates
Banks <-c( 0,
0,
0,
0,
0,
0,
0,
0,
0,
round(S_modelData$intb[yr], digits = 0), #^^
0,
round(-S_modelData$fb[yr], digits = 0),
0,
round(S_modelData$opb[yr], digits = 0),
round(S_modelData$hbd[yr]-S_modelData$hbd[yr-1], digits = 0),
round(-(S_modelData$ms[yr]-S_modelData$ms[yr-1]), digits = 0),
round(S_modelData$bb[yr]-S_modelData$bb[yr-1], digits = 0),
round(S_modelData$ls[yr]-S_modelData$ls[yr-1], digits = 0),
0,
round(S_modelData$oab[yr]-S_modelData$oab[yr-1], digits = 0),
round(S_modelData$vb[yr]-S_modelData$vb[yr-1], digits = 0),
paste(round(S_modelData$opb[yr]-(S_modelData$vb[yr]-S_modelData$vb[yr-1])+S_modelData$intb[yr]-S_modelData$fb[yr], digits = 0)))
#Create table of results
BankData<-as.data.frame(Banks,row.names=rownames)
#Print banks column
kable(BankData)
################################################################################
#Create ECB aggregates
ECB <-c( 0,
0,
0,
0,
0,
0,
0,
0,
0,
round(S_modelData$fcb[yr], digits = 0), #
0,
0,
round(-S_modelData$fcb[yr], digits = 0), #
round(S_modelData$opcb[yr], digits = 0),
round(-(S_modelData$hs[yr]-S_modelData$hs[yr-1]), digits = 0),
0,
round((S_modelData$bcb[yr]-S_modelData$bcb[yr-1]), digit = 0),
0,
0,
round(S_modelData$oacb[yr]-S_modelData$oacb[yr-1], digits = 0),
round(S_modelData$vcb[yr]-S_modelData$vcb[yr-1], digits = 0),
paste(round(S_modelData$opcb[yr]-(S_modelData$vcb[yr]-S_modelData$vcb[yr-1]), digits = 0)))
#Create table of results
CBData<-as.data.frame(ECB,row.names=rownames)
#Print ECB column
kable(CBData)
################################################################################
#Create government aggregates
Government <-c( 0,
0,
round(-S_modelData$gov[yr], digits = 0),
0,
0,
0,
round(S_modelData$tax[yr], digits = 0),
round(-S_modelData$tr[yr], digits = 0),
0,
round(-(S_modelData$intg[yr]), digits = 0),
0,
0,
round(S_modelData$fcb[yr], digits = 0),
round(S_modelData$opg[yr], digits = 0),
0,
0,
round(-(S_modelData$bs[yr]-S_modelData$bs[yr-1]), digits = 0),
0,
0,
round(S_modelData$oag[yr]-S_modelData$oag[yr-1], digits = 0),
round(S_modelData$vg[yr]-S_modelData$vg[yr-1], digits = 0),
paste(round(-S_modelData$gov[yr]+S_modelData$tax[yr]-S_modelData$tr[yr]-(S_modelData$intg[yr])+S_modelData$fcb[yr]+S_modelData$opg[yr]-(S_modelData$vg[yr]-S_modelData$vg[yr-1]), digits = 0)))
#Create table of results
GovData<-as.data.frame(Government,row.names=rownames)
#Print government column
kable(GovData)
################################################################################
#Create households aggregates
Households <-c( round(-S_modelData$cons[yr], digits = 0),
0,
0,
0,
0,
0,
round(-S_modelData$tax[yr], digits = 0),
round(S_modelData$tr[yr], digits = 0),
round(S_modelData$wb[yr], digits = 0),
round(S_modelData$inth[yr], digits = 0),
round(S_modelData$fdf[yr], digits = 0),
round(S_modelData$fb[yr], digits = 0),
0,
round(S_modelData$oph[yr], digits = 0),
round(S_modelData$hh[yr]-S_modelData$hh[yr-1], digits = 0),
round(S_modelData$mh[yr]-S_modelData$mh[yr-1], digits = 0),
round(S_modelData$bh[yr]-S_modelData$bh[yr-1], digits = 0),
round(-(S_modelData$lh[yr]-S_modelData$lh[yr-1]), digits = 0),
round(S_modelData$eh[yr]-S_modelData$eh[yr-1], digits = 0),
round(S_modelData$oah[yr]-S_modelData$oah[yr-1], digits = 0),
round(S_modelData$vh[yr]-S_modelData$vh[yr-1], digits = 0),
paste(round(-S_modelData$cons[yr]-S_modelData$tax[yr]+S_modelData$tr[yr]+S_modelData$wb[yr]+S_modelData$inth[yr]+S_modelData$fdf[yr]+S_modelData$fb[yr]+S_modelData$oph[yr]-(S_modelData$vh[yr]-S_modelData$vh[yr-1]), digits = 0)))
#Create table of results
HouseData<-as.data.frame(Households,row.names=rownames)
#Print households column
kable(HouseData)
################################################################################
#Create Foreign sector aggregates
Foreign <-c( 0,
0,
0,
round(-S_modelData$x[yr], digits = 0),
round(S_modelData$im[yr], digits = 0),
0,
0,
0,
0,
round(S_modelData$introw[yr], digits = 0),
0,
0,
0,
round(S_modelData$oprow[yr], digits = 0),
0,
0,
round(S_modelData$brow[yr]-S_modelData$brow[yr-1], digits = 0),
0,
0,
round(S_modelData$oarow[yr]-S_modelData$oarow[yr-1], digits = 0),
round(S_modelData$vrow[yr]-S_modelData$vrow[yr-1], digits = 0),
paste(round(-S_modelData$x[yr]+S_modelData$im[yr]+S_modelData$introw[yr]+S_modelData$oprow[yr]-(S_modelData$vrow[yr]-S_modelData$vrow[yr-1]), digits = 0)))
#Create table of results
ROWData<-as.data.frame(Foreign,row.names=rownames)
#Print foreign sector column
kable(ROWData)
################################################################################
#Create row total
Total <-c( 0,
0,
0,
0,
0,
round(S_modelData$y[yr]-(S_modelData$cons[yr]+S_modelData$id[yr]+S_modelData$gov[yr]+S_modelData$x[yr]-S_modelData$im[yr]), digits = 0),
0,
0,
0,
round(-S_modelData$intf[yr]+S_modelData$fcb[yr]-S_modelData$intg[yr]+S_modelData$inth[yr]+S_modelData$introw[yr]+S_modelData$intb[yr], digits = 0),
0,
0,
0,
round(S_modelData$oph[yr]+S_modelData$opf[yr]+S_modelData$opg[yr]+S_modelData$opb[yr]+
+S_modelData$opcb[yr]+S_modelData$oprow[yr], digits = 0),
round((S_modelData$hh[yr]-S_modelData$hh[yr-1])+(S_modelData$hbd[yr]-S_modelData$hbd[yr-1])-(S_modelData$hs[yr]-S_modelData$hs[yr-1]), digits = 0),
round((S_modelData$mh[yr]-S_modelData$mh[yr-1])-(S_modelData$ms[yr]-S_modelData$ms[yr-1]), digits = 0),
round((S_modelData$bh[yr]-S_modelData$bh[yr-1])-(S_modelData$bs[yr]-S_modelData$bs[yr-1])+
(S_modelData$bb[yr]-S_modelData$bb[yr-1])+((S_modelData$bcb[yr])-(S_modelData$bcb[yr-1]))+
(S_modelData$brow[yr]-S_modelData$brow[yr-1]), digits = 0),
round(-(S_modelData$lh[yr]-S_modelData$lh[yr-1])-(S_modelData$lf[yr]-S_modelData$lf[yr-1])+(S_modelData$ls[yr]-S_modelData$ls[yr-1]), digit = 0),
round((S_modelData$es[yr]-S_modelData$es[yr-1])-(S_modelData$eh[yr]-S_modelData$eh[yr-1]), digits = 0),
round((S_modelData$oah[yr]-S_modelData$oah[yr-1])+(S_modelData$oaf[yr]-S_modelData$oaf[yr-1])+(S_modelData$oag[yr]-S_modelData$oag[yr-1])+
+(S_modelData$oab[yr]-S_modelData$oab[yr-1])+(S_modelData$oacb[yr]-S_modelData$oacb[yr-1])+(S_modelData$oarow[yr]-S_modelData$oarow[yr-1]), digits = 0),
round((S_modelData$vh[yr]-S_modelData$vh[yr-1])+(S_modelData$vf[yr]-S_modelData$vf[yr-1])+(S_modelData$vg[yr]-S_modelData$vg[yr-1])+
+(S_modelData$vb[yr]-S_modelData$vb[yr-1])+(S_modelData$vcb[yr]-S_modelData$vcb[yr-1])+(S_modelData$vrow[yr]-S_modelData$vrow[yr-1]), digits = 0),
0)
#Create table of results
TotalData<-as.data.frame(Total,row.names=rownames)
#Print banks column
kable(TotalData)
################################################################################
#Create TFM matrix
Italy_TFM_Matrix<-cbind(HouseData,FirmData_c,FirmData_k,GovData,BankData,CBData,ROWData,TotalData)
kable(Italy_TFM_Matrix)
################################################################################
#Upload libraries
library(knitr)
library(kableExtra)
#Create caption
captionTFM <- paste("Table 2. Transactions-flow matrix in period", yr+1994)
#Create html table for TFM
Italy_TFM_Matrix %>%
kbl(caption=captionTFM,
format= "html",
#format= "latex",
col.names = c("Households","Firms (current)","Firms (capital)","Government","Banks","ECB","Foreign","Total"),
align="r") %>%
kable_classic(full_width = F, html_font = "helvetica")The associated tables are those displayed in Section 1.
The model is now ready to perform simulations. In fact, we can use in-sample simulations of model variables to verify how well the model replicates observed data for the past years. The first step is to define the exogenization list, which comprises the variables kept exogenous in the simulations. In this regard, we have chosen the variables named 'Other payments', 'Other financial assets', the policy rate, the foreign price level, and the energy price level. The associated code chunk is:
# Define exogenization list to 2021
exogenizeList <- list(
#Adjusted endogenous variables in 1998-2021
oph = TRUE, #Other payments associated with households
opf = TRUE, #Other payments associated with firms
opb = TRUE, #Other payments associated with banks
opcb = TRUE, #Other payments associated with ECB
oacb = TRUE, #Other financial assets of ECB
oaf = TRUE, #Other financial assets held by firms
oab = TRUE, #Other financial assets held by banks
oag = TRUE, #Other financial assets held by government
oah = TRUE, #Other financial assets held by households
rstar = TRUE, #ECB refinancing rate
Lp_row = TRUE, #Log of foreign price level
Lp_en = TRUE #Log of price of energy
)In-sample unadjusted simulations can be generated simply by running the following additional code:
# In-sample prediction (no add factors)
S_model <- SIMULATE(S_model
,simType='STATIC'
,TSRANGE=c(1998,1,2021,1)
,simConvergence=0.00001
,simIterLimit=100
,Exogenize=exogenizeList,
verbose = FALSE )Since we are conducting an in-sample simulation, we use a static prediction approach. This means that historical values for the lagged endogenous variables are utilised in the solutions of subsequent periods.
Note: A dynamic prediction can also be performed. All it takes is to replace STATIC with DYNAMIC (or FORECAST) in the code chunk above. However, the presence of several structural breaks in the period considered (e.g., the launch of the euro, three financial crises, and the Covid-19 crisis) is likely to worsen the model fit even beyond its shortcomings. In principle, this problem can be partly addressed by exogenising variables reflecting the shocks or using dummy variables.
Having clarified this, we can now plot the observed series against the simulated one for each variable.
#Define layout
layout(matrix(c(1,2,3,4,5,6,7,8,9), 3, 3, byrow = TRUE))
#Define colour of simulated series
color <- "red1"
# Show predicted Nominal GDP
plot(S_model$simulation$y,col=color,lty=1,lwd=1,font.main=1,cex.main=1,main="(a) Nominal GDP (constant prices)",ylab = 'Million Euro',xlab = '', cex.axis=1,cex.lab=1,xlim=range(1998,2020),ylim=range(min(S_modelData$y),max(S_model$simulation$y)))
lines(S_modelData$y,col="darkorchid4",lty=3,lwd=3)
legend("bottom",c("Observed","Simulated"), bty = "n", cex=1, lty=c(3,1), lwd=c(3,1), col = c("darkorchid4",color), box.lty=0)
abline(h=1795100,col=4)
# Show predicted Nominal consumption
plot(S_model$simulation$consR,col=color,lty=1,lwd=1,font.main=1,cex.main=1,main="(b) Nominal consumption (constant prices)",ylab = 'Million Euro',xlab = '', cex.axis=1,cex.lab=1,xlim=range(1998,2020),ylim=range(min(S_modelData$cons),max(S_model$simulation$cons)))
lines(S_modelData$consR,col="darkorchid4",lty=3,lwd=3)
legend("bottom",c("Observed","Simulated"), bty = "n", cex=1, lty=c(3,1), lwd=c(3,1), col = c("darkorchid4",color), box.lty=0)
# Show predicted Nominal investment
plot(S_model$simulation$id,col=color,lty=1,lwd=1,font.main=1,cex.main=1,main="(c) Nominal investment (constant prices)",ylab = 'Million Euro',xlab = '', cex.axis=1,cex.lab=1,xlim=range(1998,2020),ylim=range(min(S_modelData$id),max(S_model$simulation$id)))
lines(S_modelData$id,col="darkorchid4",lty=3,lwd=3)
legend("bottom",c("Observed","Simulated"), bty = "n", cex=1, lty=c(3,1), lwd=c(3,1), col = c("darkorchid4",color), box.lty=0)
# Show predicted import
plot(S_model$simulation$im,col=color,lty=1,lwd=1,font.main=1,cex.main=1,main="(d) Nominal import (constant prices)",ylab = 'Million Euro',xlab = '', cex.axis=1,cex.lab=1,xlim=range(1998,2020),ylim=range(min(S_modelData$im),max(S_model$simulation$im)))
lines(S_modelData$im,col="darkorchid4",lty=3,lwd=3)
legend("bottom",c("Observed","Simulated"), bty = "n", cex=1, lty=c(3,1), lwd=c(3,1), col = c("darkorchid4",color), box.lty=0)
# Show predicted export
plot(S_model$simulation$x,col=color,lty=1,lwd=1,font.main=1,cex.main=1,main="(e) Nominal export (constant prices)",ylab = 'Million Euro',xlab = '', cex.axis=1,cex.lab=1,xlim=range(1998,2020),ylim=range(min(S_modelData$x),max(S_model$simulation$x)))
lines(S_modelData$x,col="darkorchid4",lty=3,lwd=3)
legend("bottom",c("Observed","Simulated"), bty = "n", cex=1, lty=c(3,1), lwd=c(3,1), col = c("darkorchid4",color), box.lty=0)
# Show predicted employment
plot(S_model$simulation$nd,col=color,lty=1,lwd=1,font.main=1,cex.main=1,main="(f) Employment",ylab = 'Number of employees',xlab = '', cex.axis=1,cex.lab=1,xlim=range(1998,2020),ylim=range(20000,24000))
lines(S_modelData$nd,col="darkorchid4",lty=3,lwd=3)
legend("bottom",c("Observed","Simulated"), bty = "n", cex=1, lty=c(3,1), lwd=c(3,1), col = c("darkorchid4",color), box.lty=0)
# Return rate on bonds
plot(100*S_model$simulation$rb,col=color,lty=1,lwd=1,font.main=1,cex.main=1,main="(g) Average yield on gov. securities",ylab = '%',xlab = '', cex.axis=1,cex.lab=1,xlim=range(1998,2020),ylim=range(0,9))
lines(100*S_modelData$rb,col="darkorchid4",lty=3,lwd=3)
legend("bottom",c("Observed","Simulated"), bty = "n", cex=1, lty=c(3,1), lwd=c(3,1), col = c("darkorchid4",color), box.lty=0)
# Debt to GDP ratio
plot(100*S_model$simulation$deb/S_model$simulation$y,col=color,lty=1,lwd=1,font.main=1,cex.main=1,main="(h) Government debt to GDP ratio",ylab = '%',xlab = '', cex.axis=1,cex.lab=1,xlim=range(1998,2020),ylim=range(95,160))
lines(100*S_modelData$deb/S_modelData$y,col="darkorchid4",lty=3,lwd=3)
legend("bottom",c("Observed","Simulated"), bty = "n", cex=1, lty=c(3,1), lwd=c(3,1), col = c("darkorchid4",color), box.lty=0)
# GDP deflator
plot(S_model$simulation$p,col=color,lty=1,lwd=1,font.main=1,cex.main=1,main="(i) Price level (GDP deflator)",ylab = 'Index (2015=100)',xlab = '', cex.axis=1,cex.lab=1,xlim=range(1998,2020),ylim=range(70,110))
lines(S_modelData$p,col="darkorchid4",lty=3,lwd=3)
legend("bottom",c("Observed","Simulated"), bty = "n", cex=1, lty=c(3,1), lwd=c(3,1), col = c("darkorchid4",color), box.lty=0)The figure below shows selected flow variables and ratios over the period 1998-2021.
While the primary goal of our model is not to outperform existing prediction models (but rather to provide a new tool for creating and comparing alternative scenarios), it tracks past data reasonably well. The main issue appears to be the inclusion of annual lags, causing model predictions to lag when the static simulation is performed. Arguably, this drawback can be overcome by using quarterly data, although seasonality and data availability issues may arise in this case.
After checking the model's fit, in-sample predictions can be adjusted to the observed series using prediction errors. This is done by exogenizing the endogenous variables of the model.
# Define exogenization list to 2021
exogenizeList <- list(
#Adjusted endogenous variables in 1998-2021
Lpc = c(1998,1,2021,1), #Log of consumer price index
Lp_en = c(1998,1,2021,1), #Log of price of energy
mul = c(1998,1,2021,1), #Markup on loans to firms
mulh = c(1998,1,2021,1), #Markup on personal loans
mubb = c(1998,1,2021,1), #Average premium on bills held by banks
mubrow = c(1998,1,2021,1), #Average premium on bills held by foreign sector
mubh = c(1998,1,2021,1), #Average premium on bills held by households
fuf = c(1998,1,2021,1), #Firms undistributed profit
lh = c(1998,1,2021,1), #Personal loans to households
gov = c(1998,1,2021,1), #Government spending
tr = c(1998,1,2021,1), #Transfers
Leh = c(1998,1,2021,1), #Log of household demand for shares
Lbh = c(1998,1,2021,1), #Log of household demand for government bills
Lhh = c(1998,1,2021,1), #Log of household demand for cash
Lbb = c(1998,1,2021,1), #Log of bank demand for bills
prod = c(1998,1,2021,1), #Labour productivity
Lns = c(1998,1,2021,1), #Log of labour force
gw = c(1998,1,2021,1), #Growth rate of wages
Lp = c(1998,1,2021,1), #Log of price level
LidR = c(1998,1,2021,1), #Log of real investment
LimR = c(1998,1,2021,1), #Log of real import
LconsR = c(1998,1,2021,1), #Log of real consumption
intmh = c(1998,1,2021,1), #Interests received by households on bank deposits
rstar = c(1998,1,2021,1), #ECB refinancing rate
tax = c(1998,1,2021,1), #Tax revenue
LxR = c(1998,1,2021,1), #Log of real export
Lp_im = c(1998,1,2021,1), #Log of price of import
Lp_row = c(1998,1,2021,1), #Log of foreign price level
oph = TRUE, #Other payments associated with households
oacb = TRUE, #Other financial assets of ECB
oaf = TRUE, #Other financial assets held by firms
oab = TRUE, #Other financial assets of banks
oag = TRUE, #Other financial assets of government
oah = TRUE, #Other financial assets of households
mub = TRUE, #Average premium paid by the government
perc_en = TRUE, #Percentage of energy import to total import
lambdarow = TRUE, #Share of government bills held by foreign sector
yf = TRUE, #Foreign income
rho = TRUE #Reserve ratio
)
# Simulate again model
S_model <- SIMULATE(S_model
,simType='STATIC'
,TSRANGE=c(1998,1,2021,1)
,simConvergence=0.00001
,simIterLimit=100
,Exogenize=exogenizeList
,quietly=TRUE)The figure below shows the adjusted values of selected flow variables and ratios over the period 1998-2021.
The model allows performing out-of-sample predictions, which can be used as the baseline scenario.
The first step is to extend exogenous variables up to the end of the forecasting period, which, in this exercise, is 2028.
# Extend exogenous and conditionally evaluated variables up to 2028
S_model$modelData <- within(S_model$modelData,{
dum = TSEXTEND(dum, UPTO=c(2028,1)) #Dummy for Bb
})Note: the only exogenous variable to be extended is the dummy variable named
Similar to what we did for adjusted in-sample predictions, the second step is to create an 'exogenization list', encompassing all the endogenous variables of the model. These variables are adjusted up to 2021 and then set free to follow the dynamics implied by the model equations.
# Define exogenization list to 2021
exogenizeList <- list(
Lpc = c(1998,1,2021,1), #Log of consumer price index
Lp_en = c(1998,1,2021,1), #Log of price of energy
mul = c(1998,1,2021,1), #Markup on loans to firms
mulh = c(1998,1,2021,1), #Markup on personal loans
mubb = c(1998,1,2021,1), #Average premium on bills held by banks
mubrow = c(1998,1,2021,1), #Average premium on bills held by foreign sector
mubh = c(1998,1,2021,1), #Average premium on bills held by households
fuf = c(1998,1,2021,1), #Firms undistributed profit
lh = c(1998,1,2021,1), #Personal loans to households
gov = c(1998,1,2021,1), #Government spending
tr = c(1998,1,2021,1), #Transfers
prod = c(1998,1,2021,1), #Labour productivity
Lns = c(1998,1,2021,1), #Log of labour force
gw = c(1998,1,2021,1), #Growth rate of wages
Lp = c(1998,1,2021,1), #Log of price level
LidR = c(1998,1,2021,1), #Log of real investment
intmh = c(1998,1,2021,1), #Interests received by households on bank deposits
rstar = c(1998,1,2021,1), #ECB refinancing rate
LimR = c(1998,1,2021,1), #Log of real import
LxR = c(1998,1,2021,1), #Log of real export
tax = c(1998,1,2021,1), #Tax revenue
Leh = c(1998,1,2021,1), #Log of household demand for shares
Lhh = c(1998,1,2021,1), #Log of household demand for cash
Lbh = c(1998,1,2021,1), #Log of household demand for government bills
Lbb = c(1998,1,2021,1), #Log of bank demand for bills
LconsR = c(1998,1,2021,1), #Log of real consumption
yf = c(1998,1,2021,1), #Foreign income
perc_en = c(1998,1,2021,1), #Percentage of energy import to total import
lambdarow = c(1998,1,2021,1), #Share of government bills held by foreign agents
mub = c(1998,1,2021,1), #Average premium paid by the government
Lp_im = c(1998,1,2021,1), #Log of price of import
Lp_row = c(1998,1,2021,1), #Log of foreign price level
oph = TRUE, #Other payments associated with households
oacb = TRUE, #Other financial assets of ECB
oaf = TRUE, #Other financial assets held by firms
oab = TRUE, #Other financial assets of banks
oag = TRUE, #Other financial assets of government
oah = TRUE, #Other financial assets of households
rho = TRUE, #Reserve ratio
exr = TRUE #Exchange rate
)The next step is to create the list of 'add factors', encompassing both the necessary adjustments to align with the 2022 series as predicted by the Italian government and other major institutions (for which we did not have all the series from Eurostat) and the expected shocks and institutional changes.
# Define add-factor list (defining exogenous adjustments: policy + available predictions)
constantAdjList <- list(
#Adjustments for 2022
Lp = TIMESERIES(0,-0.017,-0.01,0.006,0.018,0.03, 0.04,0.045,START=c(2021,1), FREQ='A'), #GDP deflator correction
LimR = TIMESERIES(0,0.156,0.156-0.031,0.156-0.045,0.156-0.045,0.156-0.045,0.156-0.045,0.156-0.045,START=c(2021,1), FREQ='A'),
LxR = TIMESERIES(0,0.075,0.075-0.012,0.075-0.01,0.075-0.01,0.075-0.01,0.075-0.01,0.075-0.01,START=c(2021,1), FREQ='A'),
LconsR = TIMESERIES(0,0,0.01,0.05,0.05,0.05,0.045,0.045, START=c(2021,1), FREQ='A'),
deltak = TIMESERIES(0,0.0126,0.0069,0.0011,-0.0016,-0.0033,-0.0033,-0.0033,START=c(2021,1), FREQ='A'),
#Shocks and institutional changes
Lp_en = TIMESERIES(0,0.38,0.055,0.06,0,0,0,0, START=c(2021,1), FREQ='A'), #Shock to energy price log-level
rstar = TIMESERIES(-0.01858333+0,-0.01858333+0.0156,-0.01858333+0.038,-0.01858333+0.03,-0.01858333+0.025,-0.01858333+0.025,-0.01858333+0.025,-0.01858333+0.025 ,START=c(2021,1), FREQ='A'),
mub = TIMESERIES(0,-0.004,-0.02,-0.014,-0.010,-0.008,-0.008,-0.008 ,START=c(2021,1), FREQ='A') )Afterward, we simulate the model out of sample using the function DYNAMIC, which employs simulated values for the lagged endogenous variables in the solutions of subsequent periods.
# Simulate model
S_model <- SIMULATE(S_model
,simType='DYNAMIC' #'FORECAST'
,TSRANGE=c(1998,1,2028,1)
,simConvergence=0.00001
,simIterLimit=1000
,Exogenize=exogenizeList
,ConstantAdjustment=constantAdjList
,quietly=TRUE)A few amendments to the plotting chunk used in Section 3 allow extending the chart of the selected variables (here expressed in real terms) until 2028.
The definition of the model baseline is complete. Before we move to alternative scenarios, additional diagrams and tables can be created.
One may want to double-check whether the model remains consistent when it is simulated out of sample. This can be done in two ways. The first is to modify slightly the code used in Section 2 to create the accounting matrices. All it takes is to replace S_modelData with S_model$simulation as a preamble for each model variable. The reference year must be adjusted as well. For instance, the predicted balance sheet and transactions-flow matrix for Italy in 2025 are, respectively:
An alternative method to verify model consistency is to create a checking mechanism based on the redundant equation of the model (
#Create consistency statement
error=0
for (i in 1:31){ error = error + (S_model$simulation$hs[i]-S_model$simulation$hd[i])^2 }
if ( error<0.1 ){cat(" *************************************************************** \n Good news! The model is watertight!. Error =", error, "< 0.1 \n ***************************************************************")} else{
if ( error<1 ){cat(" ******************************************************** \n Double-check model consistency. Error =", error, "> 0.1 \n ********************************************************")}
else{cat(" *************************************************************** \n Warning: the model is not fully consistent! Error =", error, "> 1 \n ***************************************************************")} } which, in this case, yields:
***************************************************************
Good news! The model is watertight!. Error = 0.04068899 < 0.1
***************************************************************Note that a small error is always likely to be present due to rounding.
Lastly, note that a more sophisticated representation of the transactions-flow matrix for a specific year (here 2021) can be obtained using a Sankey diagram:
This diagram illustrates that each flow (and change in stock) originates from somewhere and goes to somewhere. The related code is:
#Choose a year. Note: 1 = 1998, 26 = 2021
yr=26
#Upload libraries for Sankey diagram
library(networkD3)
library(htmlwidgets)
library(htmltools)
#Create nodes: source, target and flows
nodes = data.frame("name" =
c("Firms outflow", # Node 0
"Banks outflow", # Node 1
"ECB outflow", # Node 2
"Government outflow", # Node 3
"Households outflow", # Node 4
"Foreign outflow", # Node 5
"Firms inflow", # Node 6
"Banks inflow", # Node 7
"ECB inflow", # Node 8
"Government inflow", # Node 9
"Households inflow", # Node 10
"Foreign inflow", # Node 11
"Consumption", # Node 12
"Investment", # Node 13
"Government spending", # Node 14
"Export", # Node 15
"Other import", # Node 16
"Taxes", # Node 17
"Transfers", # Node 18
"Wages", # Node 19
"Interest payments", # Node 20
"Corporate profit", # Node 21
"Bank profit", # Node 22
"CB seigniorage", # Node 23
"Other payments", # Node 24
"Change in net wealth", # Node 25
"Gross energy import" #Node 26
))
#Create the flows
links = as.data.frame(matrix(c(
4, 12, S_model$simulation$cons[yr],
12, 6, S_model$simulation$cons[yr],
0, 13, S_model$simulation$id[yr],
13, 6, S_model$simulation$id[yr],
3, 14, S_model$simulation$gov[yr],
14, 6, S_model$simulation$gov[yr],
5, 15, S_model$simulation$x[yr],
15, 6, S_model$simulation$x[yr],
0, 16, S_model$simulation$im[yr]-S_model$simulation$im_en[yr],
16, 11, S_model$simulation$im[yr]-S_model$simulation$im_en[yr],
0, 26, S_model$simulation$im_en[yr],
26, 11, S_model$simulation$im_en[yr],
4, 17, S_model$simulation$tax[yr],
17, 9, S_model$simulation$tax[yr],
3, 18, S_model$simulation$tr[yr],
18, 10, S_model$simulation$tr[yr],
0, 19, S_model$simulation$wb[yr],
19, 10, S_model$simulation$wb[yr],
0, 20, S_model$simulation$intf[yr],
3, 20, S_model$simulation$intg[yr],
20, 7, S_model$simulation$fb[yr],
20, 8, S_model$simulation$fcb[yr],
20, 10, S_model$simulation$inth[yr],
0, 21, S_model$simulation$fdf[yr],
21, 10, S_model$simulation$fdf[yr],
1, 22, S_model$simulation$fb[yr],
22, 10, S_model$simulation$fb[yr],
2, 23, S_model$simulation$fcb[yr],
23, 9, S_model$simulation$fcb[yr],
0, 24, if (S_model$simulation$opf[yr]<0){-S_model$simulation$opf[yr]}else{0},
1, 24, if (S_model$simulation$opb[yr]<0){-S_model$simulation$opb[yr]}else{0},
2, 24, if (S_model$simulation$opcb[yr]<0){-S_model$simulation$opcb[yr]}else{0},
3, 24, if (S_model$simulation$opg[yr]<0){-S_model$simulation$opg[yr]}else{0},
4, 24, if (S_model$simulation$oph[yr]<0){-S_model$simulation$oph[yr]}else{0},
5, 24, if (S_model$simulation$oprow[yr]<0){-S_model$simulation$oprow[yr]}else{0},
24, 6, if (S_model$simulation$opf[yr]>=0){S_model$simulation$opf[yr]}else{0},
24, 7, if (S_model$simulation$opb[yr]>=0){S_model$simulation$opb[yr]}else{0},
24, 8, if (S_model$simulation$opcb[yr]>=0){S_model$simulation$opcb[yr]}else{0},
24, 9, if (S_model$simulation$opg[yr]>=0){S_model$simulation$opg[yr]}else{0},
24, 10, if (S_model$simulation$oph[yr]>=0){S_model$simulation$oph[yr]}else{0},
24, 11, if (S_model$simulation$oprow[yr]>=0){S_model$simulation$oprow[yr]}else{0},
0, 25, if (S_model$simulation$vf[yr]-S_model$simulation$vf[yr-1]<0){-S_model$simulation$vf[yr]+S_model$simulation$vf[yr-1]}else{0},
1, 25, if (S_model$simulation$vb[yr]-S_model$simulation$vb[yr-1]<0){-S_model$simulation$vb[yr]+S_model$simulation$vb[yr-1]}else{0},
2, 25, if (S_model$simulation$vcb[yr]-S_model$simulation$vcb[yr-1]<0){-S_model$simulation$vcb[yr]+S_model$simulation$vcb[yr-1]}else{0},
3, 25, if (S_model$simulation$vg[yr]-S_model$simulation$vg[yr-1]<0){-S_model$simulation$vg[yr]+S_model$simulation$vg[yr-1]}else{0},
4, 25, if (S_model$simulation$vh[yr]-S_model$simulation$vh[yr-1]<0){-S_model$simulation$vh[yr]+S_model$simulation$vh[yr-1]}else{0},
5, 25, if (S_model$simulation$vrow[yr]-S_model$simulation$vrow[yr-1]<0){-S_model$simulation$vrow[yr]+S_model$simulation$vrow[yr-1]}else{0},
25, 6, if (S_model$simulation$vf[yr]-S_model$simulation$vf[yr-1]>=0){S_model$simulation$vf[yr]-S_model$simulation$vf[yr-1]}else{0},
25, 7, if (S_model$simulation$vb[yr]-S_model$simulation$vb[yr-1]>=0){S_model$simulation$vb[yr]-S_model$simulation$vb[yr-1]}else{0},
25, 8, if (S_model$simulation$vcb[yr]-S_model$simulation$vcb[yr-1]>=0){S_model$simulation$vcb[yr]-S_model$simulation$vcb[yr-1]}else{0},
25, 9, if (S_model$simulation$vg[yr]-S_model$simulation$vg[yr-1]>=0){S_model$simulation$vg[yr]-S_model$simulation$vg[yr-1]}else{0},
25, 10, if (S_model$simulation$vh[yr]-S_model$simulation$vh[yr-1]>=0){S_model$simulation$vh[yr]-S_model$simulation$vh[yr-1]}else{0},
25, 11, if (S_model$simulation$vrow[yr]-S_model$simulation$vrow[yr-1]>=0){S_model$simulation$vrow[yr]-S_model$simulation$vrow[yr-1]}else{0}
),
byrow = TRUE, ncol = 3))
names(links) = c("source", "target", "value")
my_color <- 'd3.scaleOrdinal() .domain([]) .range(["chartreuse","red","green","yellow","dodgerblue","darkorchid","khaki","peru","violet","cyan","pink","orange","beige","gray","blue","black","darkorchid4","goldenrod4"])'
#Create and plot the network
sankeyNetwork(Links = links, Nodes = nodes,
Source = "source", Target = "target",
Value = "value", NodeID = "name", colourScale=my_color,
fontSize= 20, nodeWidth = 30)Three additional scenarios are considered and compared with the baseline scenario.
Alternative Scenario 1: The energy-led price shock has a more persistent effect on inflation, with the inflation rate (CPI) still projected to be around 5% for the foreseeable years.
Alternative Scenario 2: The economy is affected by two shocks, namely, a persistent inflation rate and a robust policy response by the ECB, which maintains the policy rate at 4.5% over the 2024-2026 period.
Alternative Scenario 3: Effects of policy austerity measures that, in accordance with the Maastricht Treaty, bring the government deficit to GDP ratio to 3% in 2024 (and subsequent years).
The scenarios are created by adding shocks to model variables in the constantAdjList. Therefore, the first scenario is obtained by exogenously increasing the (log) series of the energy price:
Lp_en = TIMESERIES(0,0.38,0.2,0.2,0.2,0.2,0.2,0.1, START=c(2021,1), FREQ='A')Similarly, the second scenario is obtained by exogenously increasing the policy rate set by the ECB, in addition to the change in the energy price index
rstar = TIMESERIES(-0.01858333+0,-0.01858333+0.0156,-0.01858333+0.038,-0.01858333+0.045,-0.01858333+0.045,-0.01858333+0.045,-0.01858333+0.045,-0.01858333+0.045 ,START=c(2021,1), FREQ='A') Moreover, the real consumption volume is adjusted downward to account for its elasticity to the policy rate, which we estimate to be 0.58. Therefore:
LconsR = TIMESERIES(0,0,0.01,0.05-0.07*(0.58/2),0.05-0.07*(0.58/2),0.05-0.07*(0.58/2),0.045-0.07*(0.58/2),0.045-0.07*(0.58/2), START=c(2021,1), FREQ='A')Finally, the third scenario is derived by cutting government spending in comparison to the baseline scenario:
gov = TIMESERIES(0,0,0,-47000,-15000,-33000,-39000,-40000, START=c(2021,1), FREQ='A')Once again, a visual representation of the experiments can be obtained by introducing a few amendments to the plotting chunk used in Section 3.
Summing up, in Alternative Scenario 1, a persistent inflation rate of around 5% leads Italy into a recession with rising unemployment, accompanied by a deterioration of public finance. By 2028, economic growth is projected to drop to -2.5%, unemployment to exceed 10%, and government debt and deficit ratios to reach 159% and 8.4%, respectively.
Alternative Scenario 2 explores similar effects of persistent inflation but with a robust ECB response, resulting in an immediate and prolonged economic recession and higher government debt and deficit ratios of 173% and 10.1% by 2028.
Lastly, Alternative Scenario 3 depicts the impact of austerity measures to comply with the 3% Maastricht rule, causing a severe recession, an annual drop of around 3% in economic growth, and an unemployment rate exceeding 15% by 2028.
This approach is recommended for experienced users. Simply execute the numbered files in sequence. We recommend executing the R code paragraph by paragraph for better clarity and control.