742

742. Closest Leaf in a Binary Tree (Medium)

Given the root of a binary tree where every node has a unique value and a target integer k, return the value of the nearest leaf node to the target k in the tree.

Nearest to a leaf means the least number of edges traveled on the binary tree to reach any leaf of the tree. Also, a node is called a leaf if it has no children.

 

Example 1:

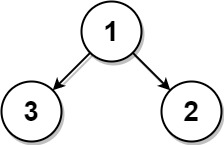
Input: root = [1,3,2], k = 1
Output: 2
Explanation: Either 2 or 3 is the nearest leaf node to the target of 1.

Example 2:

Input: root = [1], k = 1
Output: 1
Explanation: The nearest leaf node is the root node itself.

Example 3:

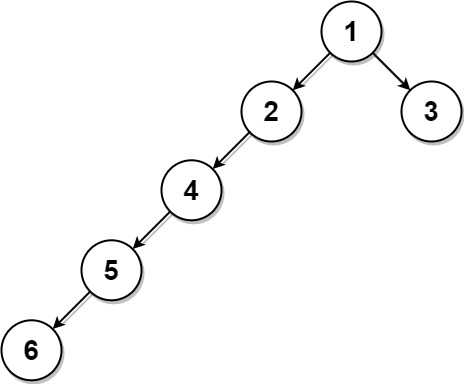
Input: root = [1,2,3,4,null,null,null,5,null,6], k = 2
Output: 3
Explanation: The leaf node with value 3 (and not the leaf node with value 6) is nearest to the node with value 2.

 

Constraints:

• The number of nodes in the tree is in the range [1, 1000].
• 1 <= Node.val <= 1000
• All the values of the tree are unique.
• There exist some node in the tree where Node.val == k.

Companies: Facebook, Databricks, Amazon

Related Topics:
Tree, Depth-First Search, Breadth-First Search, Binary Tree

Solution 1. DFS

// OJ: https://leetcode.com/problems/closest-leaf-in-a-binary-tree
// Author: github.com/lzl124631x
// Time: O(N)
// Space: O(H)
class Solution {
public:
    int findClosestLeaf(TreeNode* root, int k) {
        int Inf = 1e9, minDist = Inf, ans = -1;
        function<array<int, 3>(TreeNode*)> dfs = [&](TreeNode *root) -> array<int, 3> { // dist to target node, the depth and id of the node on the other subtree with the minimum depth
            if (!root) return {Inf, Inf, -1};
            if (!root->left && !root->right) {
                if (root->val == k) {
                    minDist = 0;
                    ans = k;
                    return {0, 0, root->val};
                }
                return {Inf, 0, root->val};
            }
            auto [a, b, c] = dfs(root->left);
            auto [d, e, f] = dfs(root->right);
            int dist = b + 1, id = c;
            if (e < b) dist = e + 1, id = f;
            if (root->val == k) {
                minDist = dist;
                ans = id;
                return {0, dist, id};
            }
            if (a >= Inf && d >= Inf) return {Inf, dist, id};
            if (d < Inf) swap(a, d), swap(b, e), swap(c, f);
            int sum = a + 1 + e;
            if (sum < minDist) {
                minDist = sum;
                ans = f;
            }
            return {a + 1, e + 1, f};
        };
        dfs(root);
        return ans;
    }
};

Solution 2. Convert to Graph

// OJ: https://leetcode.com/problems/closest-leaf-in-a-binary-tree
// Author: github.com/lzl124631x
// Time: O(N)
// Space: O(N)
class Solution {
public:
    int findClosestLeaf(TreeNode* root, int k) {
        unordered_map<int, vector<int>> G;
        unordered_set<int> leaf, seen;
        function<void(TreeNode*, TreeNode*)> convertGraph = [&](TreeNode *root, TreeNode *parent) {
            if (!root) return;
            if (parent) {
                G[parent->val].push_back(root->val);
                G[root->val].push_back(parent->val);
            }
            if (!root->left && !root->right) leaf.insert(root->val);
            convertGraph(root->left, root);
            convertGraph(root->right, root);
        };
        convertGraph(root, nullptr);
        queue<int> q{{k}};
        seen.insert(k);
        while (q.size()) {
            int cnt = q.front();
            while (cnt--) {
                int u = q.front();
                q.pop();
                if (leaf.count(u)) return u;
                for (int v : G[u]) {
                    if (seen.count(v)) continue;
                    seen.insert(v);
                    q.push(v);
                }
            }
        }
        return -1;
    }
};

Solution 3.

• Get the path from root to the target node.
• For each node in this path, find the r.node with the minimum distFromTarget + r.dist. Here distFromTarget is the distance from the target node to the current node. r.node is the closest leaf node to the current node, and r.dist is the corresponding distance between these two nodes.

// OJ: https://leetcode.com/problems/closest-leaf-in-a-binary-tree
// Author: github.com/lzl124631x
// Time: O(N)
// Space: O(N)
public:
    int findClosestLeaf(TreeNode* root, int k) {
        vector<TreeNode*> path;
        unordered_map<TreeNode*, LeafResult> annotation;
        function<bool(TreeNode*)> getPath = [&](TreeNode *root) {
            if (!root) return false;
            path.push_back(root);
            if (root->val == k) return true;
            if (getPath(root->left) || getPath(root->right)) return true;
            path.pop_back();
            return false;
        };
        getPath(root);
        function<LeafResult(TreeNode *root)> closestLeaf = [&](TreeNode *root) {
            if (!root) return LeafResult(nullptr, INT_MAX);
            if (!root->left && !root->right) return LeafResult(root, 0);
            if (annotation.count(root)) return annotation[root];
            auto L = closestLeaf(root->left);
            auto R = closestLeaf(root->right);
            return annotation[root] = LeafResult(L.dist < R.dist ? L.node : R.node, min(L.dist, R.dist) + 1);
        };
        int distFromTarget = path.size() - 1, dist = INT_MAX, ans = -1;
        for (auto n : path) {
            auto r = closestLeaf(n);
            if (r.dist + distFromTarget < dist) {
                dist = r.dist + distFromTarget;
                ans = r.node->val;
            }
            distFromTarget--;
        }
        return ans;
    }
};