2385

2385. Amount of Time for Binary Tree to Be Infected (Medium)

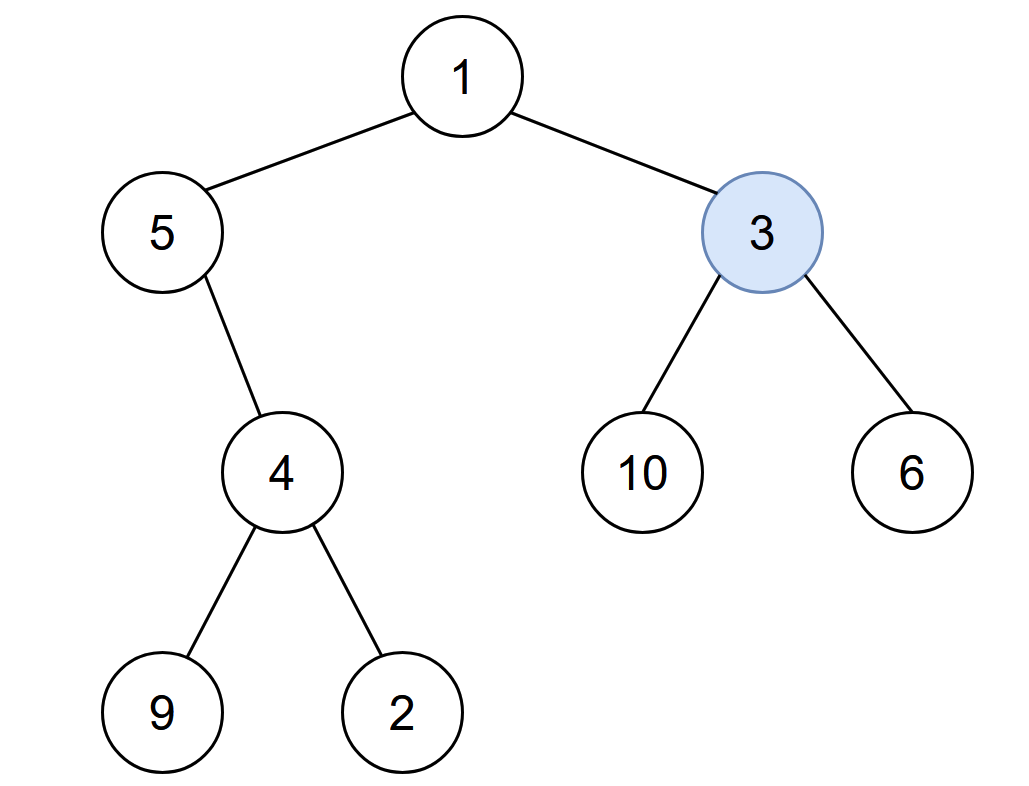
You are given the root of a binary tree with unique values, and an integer start. At minute 0, an infection starts from the node with value start.

Each minute, a node becomes infected if:

• The node is currently uninfected.
• The node is adjacent to an infected node.

Return the number of minutes needed for the entire tree to be infected.

 

Example 1:

Input: root = [1,5,3,null,4,10,6,9,2], start = 3
Output: 4
Explanation: The following nodes are infected during:
- Minute 0: Node 3
- Minute 1: Nodes 1, 10 and 6
- Minute 2: Node 5
- Minute 3: Node 4
- Minute 4: Nodes 9 and 2
It takes 4 minutes for the whole tree to be infected so we return 4.

Example 2:

Input: root = [1], start = 1
Output: 0
Explanation: At minute 0, the only node in the tree is infected so we return 0.

 

Constraints:

• The number of nodes in the tree is in the range [1, 105].
• 1 <= Node.val <= 105
• Each node has a unique value.
• A node with a value of start exists in the tree.

Related Topics:
Tree, Depth-First Search, Breadth-First Search, Binary Tree

Similar Questions:

• Maximum Depth of Binary Tree (Easy)
• Shortest Path to Get Food (Easy)
• All Nodes Distance K in Binary Tree (Easy)

Solution 1. DFS

// OJ: https://leetcode.com/problems/amount-of-time-for-binary-tree-to-be-infected
// Author: github.com/lzl124631x
// Time: O(N)
// Space: O(H)
class Solution {
public:
    int amountOfTime(TreeNode* root, int start) {
        int ans = 0, sd = -1;
        typedef pair<bool, int> PBI;
        function<PBI(TreeNode*, int)> dfs = [&](TreeNode *n, int depth) {
            if (!n) return PBI{false, 0};
            bool found = start == n->val;
            auto [lf, ld] = dfs(n->left, depth + 1);
            auto [rf, rd] = dfs(n->right, depth + 1);
            if (found) {
                sd = depth;
                ans = max(ans, max(ld, rd));
            }
            if (lf) ans = max(ans, sd - depth + rd);
            if (rf) ans = max(ans, sd - depth + ld);
            return PBI{lf || rf || found, 1 + max(ld, rd)};
        };
        dfs(root, 0);
        return ans;
    }
};