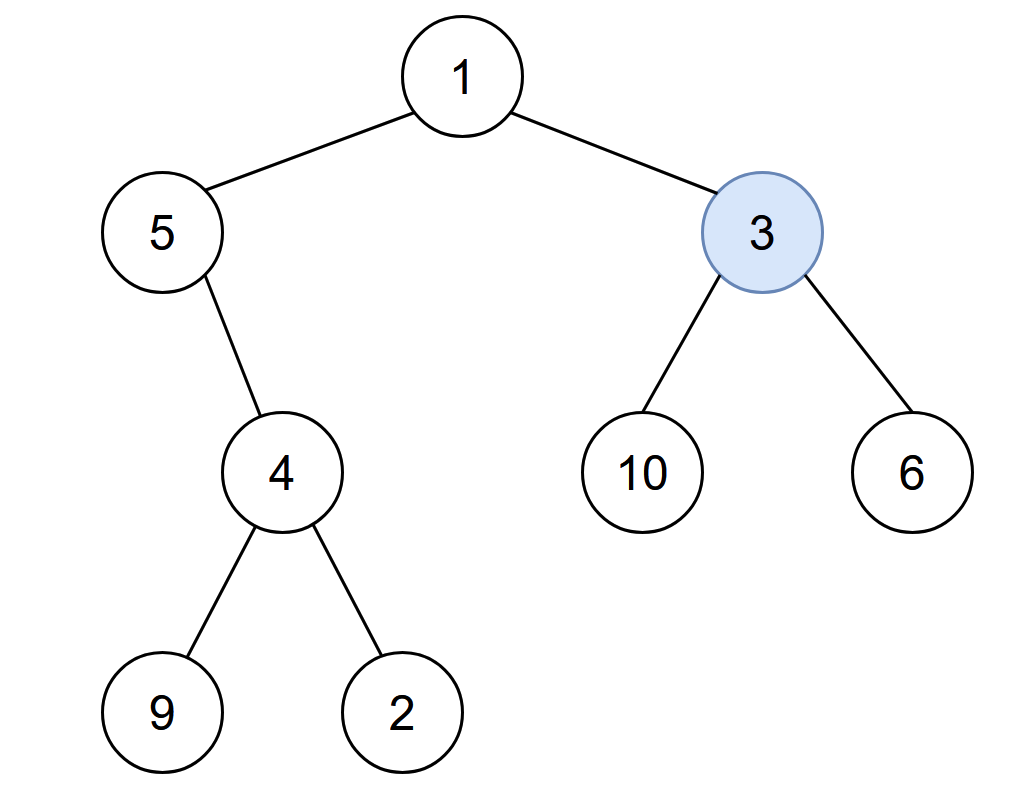
You are given the root of a binary tree with unique values, and an integer start. At minute 0, an infection starts from the node with value start.
Each minute, a node becomes infected if:
- The node is currently uninfected.
- The node is adjacent to an infected node.
Return the number of minutes needed for the entire tree to be infected.
Example 1:
Input: root = [1,5,3,null,4,10,6,9,2], start = 3 Output: 4 Explanation: The following nodes are infected during: - Minute 0: Node 3 - Minute 1: Nodes 1, 10 and 6 - Minute 2: Node 5 - Minute 3: Node 4 - Minute 4: Nodes 9 and 2 It takes 4 minutes for the whole tree to be infected so we return 4.
Example 2:
Input: root = [1], start = 1 Output: 0 Explanation: At minute 0, the only node in the tree is infected so we return 0.
Constraints:
- The number of nodes in the tree is in the range
[1, 105]. 1 <= Node.val <= 105- Each node has a unique value.
- A node with a value of
startexists in the tree.
Related Topics:
Tree, Depth-First Search, Breadth-First Search, Binary Tree
Similar Questions:
- Maximum Depth of Binary Tree (Easy)
- Shortest Path to Get Food (Easy)
- All Nodes Distance K in Binary Tree (Easy)
// OJ: https://leetcode.com/problems/amount-of-time-for-binary-tree-to-be-infected
// Author: github.com/lzl124631x
// Time: O(N)
// Space: O(H)
class Solution {
public:
int amountOfTime(TreeNode* root, int start) {
int ans = 0, sd = -1;
typedef pair<bool, int> PBI;
function<PBI(TreeNode*, int)> dfs = [&](TreeNode *n, int depth) {
if (!n) return PBI{false, 0};
bool found = start == n->val;
auto [lf, ld] = dfs(n->left, depth + 1);
auto [rf, rd] = dfs(n->right, depth + 1);
if (found) {
sd = depth;
ans = max(ans, max(ld, rd));
}
if (lf) ans = max(ans, sd - depth + rd);
if (rf) ans = max(ans, sd - depth + ld);
return PBI{lf || rf || found, 1 + max(ld, rd)};
};
dfs(root, 0);
return ans;
}
};