1727

1727. Largest Submatrix With Rearrangements (Medium)

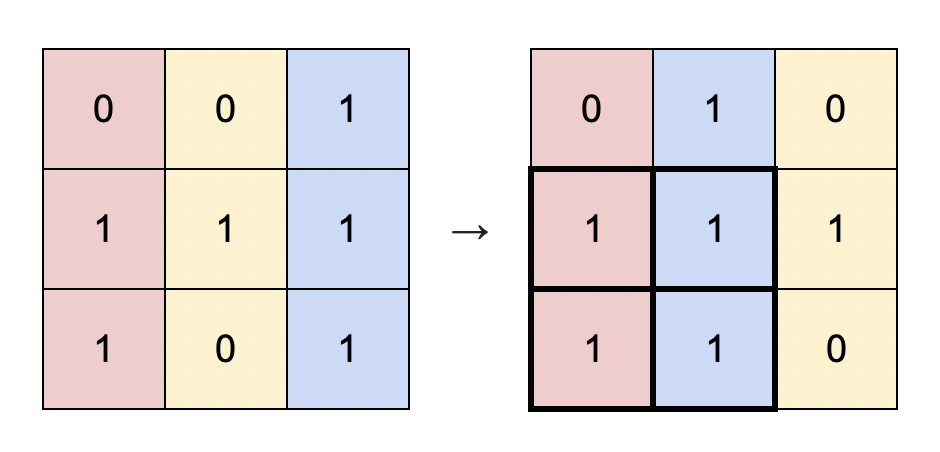
You are given a binary matrix matrix of size m x n, and you are allowed to rearrange the columns of the matrix in any order.

Return the area of the largest submatrix within matrix where every element of the submatrix is 1 after reordering the columns optimally.

 

Example 1:

Input: matrix = [[0,0,1],[1,1,1],[1,0,1]]
Output: 4
Explanation: You can rearrange the columns as shown above.
The largest submatrix of 1s, in bold, has an area of 4.

Example 2:

Input: matrix = [[1,0,1,0,1]]
Output: 3
Explanation: You can rearrange the columns as shown above.
The largest submatrix of 1s, in bold, has an area of 3.

Example 3:

Input: matrix = [[1,1,0],[1,0,1]]
Output: 2
Explanation: Notice that you must rearrange entire columns, and there is no way to make a submatrix of 1s larger than an area of 2.

 

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m * n <= 105
• matrix[i][j] is either 0 or 1.

Companies: Google, Directi

Related Topics:
Array, Greedy, Sorting, Matrix

Similar Questions:

• Max Area of Island (Medium)

Hints:

• For each column, find the number of consecutive ones ending at each position.
• For each row, sort the cumulative ones in non-increasing order and "fit" the largest submatrix.

Solution 1.

Start from a single row, the max area we can get is the number of 1s.

Now consider adding a second row, there might be columns with height 2, 1 or 0. If we can the count of these columns, we can get the corresponding area.

For example, assume there are 3 columns with height 2, 4 columns with height 1, 1 column with height 0, then we have:

• matrix with height 2 and width 3. So area is 6
• matrix with height 1 and width (3 + 1). So area is 4.j

So we can keep a vector<int> h where h[j], when visiting the i-th row, is the number of 1s from A[i][j] upwards, i.e. the height from A[i][j] upwards.

And for each row, after updating h, we count sort the heights and calculate the corresponding areas.

Time complexity

For each row:

• updating h takes O(N) time.
• udpating m takes O(NlogN) time.
• calculating the areas takes O(U) time where U <= N is the number of distinct heights.

So overall the time complexity is O(MNlogN).

// OJ: https://leetcode.com/problems/largest-submatrix-with-rearrangements/
// Author: github.com/lzl124631x
// Time: O(MNlogN)
// Space: O(N)
class Solution {
public:
    int largestSubmatrix(vector<vector<int>>& A) {
        int M = A.size(), N = A[0].size(), ans = 0;
        vector<int> h(N);
        for (int i = 0; i < M; ++i) {
            for (int j = 0; j < N; ++j) {
                h[j] = A[i][j] == 0 ? 0 : (h[j] + 1);
            }
            map<int, int> m;
            for (int n : h) m[n]++;
            int w = 0;
            for (auto it = m.rbegin(); it != m.rend(); ++it) {
                w += it->second;
                ans = max(ans, w * it->first);
            }
        }
        return ans;
    }
};

Or

// OJ: https://leetcode.com/problems/largest-submatrix-with-rearrangements
// Author: github.com/lzl124631x
// Time: O(MNlogN)
// Space: O(N)
class Solution {
public:
    int largestSubmatrix(vector<vector<int>>& A) {
        int N = A[0].size(), ans = 0;
        vector<int> h(N), id(N);
        iota(begin(id), end(id), 0);
        for (auto &r : A) {
            for (int j = 0; j < N; ++j) {
                if (r[j]) ++h[j];
                else h[j] = 0;
            }
            sort(begin(id), end(id), [&](int a, int b) { return h[a] < h[b]; });
            for (int i = 0; i < N; ++i) ans = max(ans, h[id[i]] * (N - i));
        }
        return ans;
    }
};