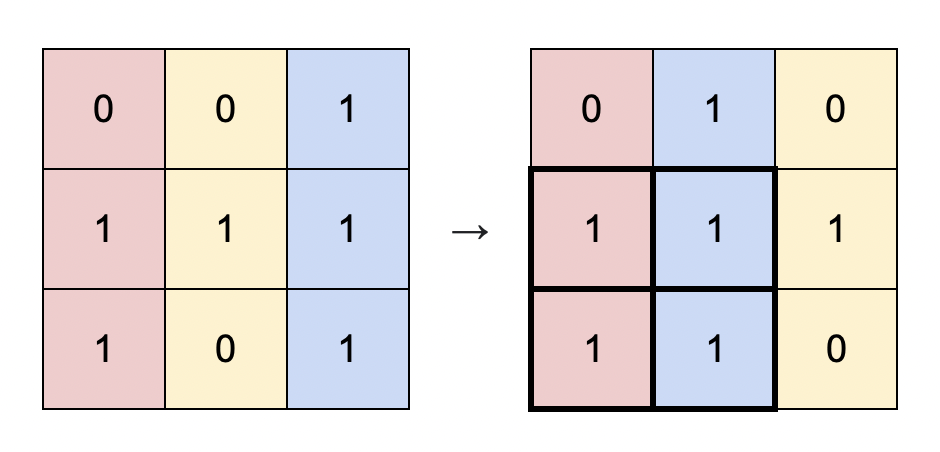
You are given a binary matrix matrix of size m x n, and you are allowed to rearrange the columns of the matrix in any order.
Return the area of the largest submatrix within matrix where every element of the submatrix is 1 after reordering the columns optimally.
Example 1:
Input: matrix = [[0,0,1],[1,1,1],[1,0,1]] Output: 4 Explanation: You can rearrange the columns as shown above. The largest submatrix of 1s, in bold, has an area of 4.
Example 2:
Input: matrix = [[1,0,1,0,1]] Output: 3 Explanation: You can rearrange the columns as shown above. The largest submatrix of 1s, in bold, has an area of 3.
Example 3:
Input: matrix = [[1,1,0],[1,0,1]] Output: 2 Explanation: Notice that you must rearrange entire columns, and there is no way to make a submatrix of 1s larger than an area of 2.
Constraints:
m == matrix.lengthn == matrix[i].length1 <= m * n <= 105matrix[i][j]is either0or1.
Related Topics:
Array, Greedy, Sorting, Matrix
Similar Questions:
Hints:
- For each column, find the number of consecutive ones ending at each position.
- For each row, sort the cumulative ones in non-increasing order and "fit" the largest submatrix.
Start from a single row, the max area we can get is the number of 1s.
Now consider adding a second row, there might be columns with height 2, 1 or 0. If we can the count of these columns, we can get the corresponding area.
For example, assume there are 3 columns with height 2, 4 columns with height 1, 1 column with height 0, then we have:
- matrix with height
2and width3. So area is6 - matrix with height
1and width(3 + 1). So area is4.j
So we can keep a vector<int> h where h[j], when visiting the i-th row, is the number of 1s from A[i][j] upwards, i.e. the height from A[i][j] upwards.
And for each row, after updating h, we count sort the heights and calculate the corresponding areas.
For each row:
- updating
htakesO(N)time. - udpating
mtakesO(NlogN)time. - calculating the areas takes
O(U)time whereU <= Nis the number of distinct heights.
So overall the time complexity is O(MNlogN).
// OJ: https://leetcode.com/problems/largest-submatrix-with-rearrangements/
// Author: github.com/lzl124631x
// Time: O(MNlogN)
// Space: O(N)
class Solution {
public:
int largestSubmatrix(vector<vector<int>>& A) {
int M = A.size(), N = A[0].size(), ans = 0;
vector<int> h(N);
for (int i = 0; i < M; ++i) {
for (int j = 0; j < N; ++j) {
h[j] = A[i][j] == 0 ? 0 : (h[j] + 1);
}
map<int, int> m;
for (int n : h) m[n]++;
int w = 0;
for (auto it = m.rbegin(); it != m.rend(); ++it) {
w += it->second;
ans = max(ans, w * it->first);
}
}
return ans;
}
};Or
// OJ: https://leetcode.com/problems/largest-submatrix-with-rearrangements
// Author: github.com/lzl124631x
// Time: O(MNlogN)
// Space: O(N)
class Solution {
public:
int largestSubmatrix(vector<vector<int>>& A) {
int N = A[0].size(), ans = 0;
vector<int> h(N), id(N);
iota(begin(id), end(id), 0);
for (auto &r : A) {
for (int j = 0; j < N; ++j) {
if (r[j]) ++h[j];
else h[j] = 0;
}
sort(begin(id), end(id), [&](int a, int b) { return h[a] < h[b]; });
for (int i = 0; i < N; ++i) ans = max(ans, h[id[i]] * (N - i));
}
return ans;
}
};