1536

1536. Minimum Swaps to Arrange a Binary Grid (Medium)

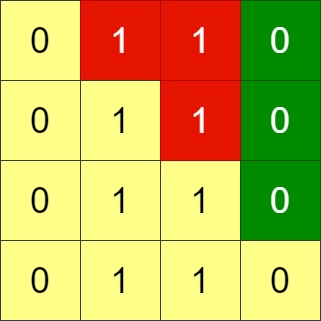
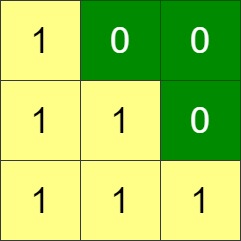
Given an n x n binary grid, in one step you can choose two adjacent rows of the grid and swap them.

A grid is said to be valid if all the cells above the main diagonal are zeros.

Return the minimum number of steps needed to make the grid valid, or -1 if the grid cannot be valid.

The main diagonal of a grid is the diagonal that starts at cell (1, 1) and ends at cell (n, n).

 

Example 1:

Input: grid = [[0,0,1],[1,1,0],[1,0,0]]
Output: 3

Example 2:

Input: grid = [[0,1,1,0],[0,1,1,0],[0,1,1,0],[0,1,1,0]]
Output: -1
Explanation: All rows are similar, swaps have no effect on the grid.

Example 3:

Input: grid = [[1,0,0],[1,1,0],[1,1,1]]
Output: 0

 

Constraints:

• n == grid.length
• n == grid[i].length
• 1 <= n <= 200
• grid[i][j] is 0 or 1

Related Topics:
Greedy

Solution 1.

First store the max index of the 1 in each row into a vector<int> v.

Then we can from the first item to the last item in v:

• if v[i] <= i, this row is good. Skip
• Otherwise, we find the minimal j (i + 1 < j < N) that satisfies v[j] <= i.
  • If we can't find it, no row can be placed at this i-th row. Return -1.
  • Otherwise, we move v[j] to v[i] and the v[k] (i <= k < j) are moved downwards. And we add j - i steps of swaps to the answer.

// https://leetcode.com/problems/minimum-swaps-to-arrange-a-binary-grid/
// Author: github.com/lzl124631x
// Time: O(N^2)
// Space: O(N)
class Solution {
public:
    int minSwaps(vector<vector<int>>& G) {
        int N = G.size(), ans = 0;
        vector<int> v(N);
        for (int i = 0; i < N; ++i) {
            int len = 0;
            for (int j = N - 1; j >= 0; --j) {
                if (G[i][j] == 0) continue;
                len = j + 1;
                break;
            }
            v[i] = len;
        }
        for (int i = 0; i < N; ++i) {
            if (v[i] <= i + 1) continue;
            int j = i + 1;
            while (j < N && v[j] > i + 1) ++j; 
            if (j == N) return -1; 
            int tmp = v[j];
            for (int k = j; k > i; --k) v[k] = v[k - 1];
            v[i] = tmp;
            ans += j - i;
        }
        return ans;
    }
};