Given an n x n binary grid, in one step you can choose two adjacent rows of the grid and swap them.
A grid is said to be valid if all the cells above the main diagonal are zeros.
Return the minimum number of steps needed to make the grid valid, or -1 if the grid cannot be valid.
The main diagonal of a grid is the diagonal that starts at cell (1, 1) and ends at cell (n, n).
Example 1:
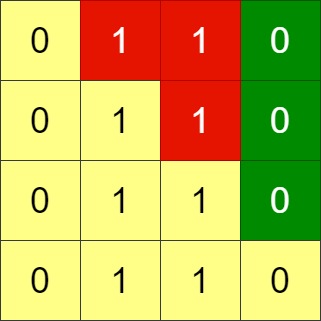
Input: grid = [[0,0,1],[1,1,0],[1,0,0]] Output: 3
Example 2:
Input: grid = [[0,1,1,0],[0,1,1,0],[0,1,1,0],[0,1,1,0]] Output: -1 Explanation: All rows are similar, swaps have no effect on the grid.
Example 3:
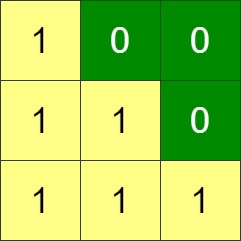
Input: grid = [[1,0,0],[1,1,0],[1,1,1]] Output: 0
Constraints:
n == grid.lengthn == grid[i].length1 <= n <= 200grid[i][j]is0or1
Related Topics:
Greedy
First store the max index of the 1 in each row into a vector<int> v.
Then we can from the first item to the last item in v:
- if
v[i] <= i, this row is good. Skip - Otherwise, we find the minimal
j(i + 1 < j < N) that satisfiesv[j] <= i.- If we can't find it, no row can be placed at this
i-th row. Return-1. - Otherwise, we move
v[j]tov[i]and thev[k](i <= k < j) are moved downwards. And we addj - isteps of swaps to the answer.
- If we can't find it, no row can be placed at this
// https://leetcode.com/problems/minimum-swaps-to-arrange-a-binary-grid/
// Author: github.com/lzl124631x
// Time: O(N^2)
// Space: O(N)
class Solution {
public:
int minSwaps(vector<vector<int>>& G) {
int N = G.size(), ans = 0;
vector<int> v(N);
for (int i = 0; i < N; ++i) {
int len = 0;
for (int j = N - 1; j >= 0; --j) {
if (G[i][j] == 0) continue;
len = j + 1;
break;
}
v[i] = len;
}
for (int i = 0; i < N; ++i) {
if (v[i] <= i + 1) continue;
int j = i + 1;
while (j < N && v[j] > i + 1) ++j;
if (j == N) return -1;
int tmp = v[j];
for (int k = j; k > i; --k) v[k] = v[k - 1];
v[i] = tmp;
ans += j - i;
}
return ans;
}
};