gobangGameABN
1.前言
2.算法介绍
1.极大极小值搜索算法(Minimax)(维基百科)
2.负极大值算法(Negamax)(维基百科)
3. -
剪枝算法(Alpha-beta pruning)(维基百科)
3.缺陷以及优化
1.运算时间复杂度
2.算杀
3.学习模块
4.总结
5.参考资料(特别感谢)
使用负值最大算法,alpha-beta剪枝算法实现的五子棋AI程序
代码仓库https://github.com/loyio/gobangGameABN
对于五子棋人机对战的程序,我一开始是尝试着使用C++进行编写的,使用SDL进行界面的渲染以及事件的处理,走棋基本算法思想是通过构建一个棋形模型组,对每一步棋进行循环,比对模型组,最终得到一个存放每个位置分值的二维数组,取里面最大分值的坐标(这里主要考虑对手方的棋型),作为电脑落子点。通过不断查阅资料,通过几个星期的构建改进,最终完成了基本功能。
后面,我通过一段时间的人机测试以及与其他五子棋AI的对战,基本得出我这个算法的优劣之处,在与人进行对战时,基本可以做到对对手方精准的防御,而且在防御的同时,能够构建己方的棋型,最终获得胜利(我个人棋艺不精),后面我选择让自己的程序与其它五子棋AI进行对战,缺点就很明显了,我的AI算法只会一昧的进行防守,而忽略了布局,基本在棋盘填到一半的时候就被别的AI算法给KO了。这里我也总结了几个原因:
1️⃣算法搜索深度太浅了,基本只搜索到第一层
2️⃣没有进行分值的组合,只采用了一方的分数
3️⃣数据结构实现太过简陋,浪费了太多的系统资源
后面我又通过查询资料,基本弄明白了博弈程序几个常用的算法,为了节省设计数据结构的时间(我的C++ STL学的还不是很深入),最终选择使用Python编写这个五子棋算法程序,在界面层渲染事件处理方面我使用的是pygame模块,比较简单,我的文档就不过多介绍。
博弈
有完备信息的,确定性的,轮流行动的,两个游戏者的零和游戏
比如象棋、围棋、五子棋等,而牌类游戏、四国军棋等无法适用
博弈树: 是指由于动态博弈参与者的行动有先后次序,因此可以依次将参与者的行动展开成一个树状图形
常见的棋类游戏的博弈树复杂度:(来自维基百科 游戏复杂度)
| 游戏 | 博弈树复杂度(以10为底数的指数部分) |
|---|---|
| 黑白棋 | 58 |
| 五子棋(15*15) | 70 |
| 国际象棋 | 123 |
| 象棋 | 150 |
| 围棋(19*19) | 360 |
下面我通过几个经典算法逐步讲解我的程序
假设:A和B对弈,轮到A走棋了,那么我们会遍历A的每一个可能走棋方法,然后对于前面A的每一个走棋方法,遍历B的每一个走棋方法,然后接着遍历A的每一个走棋方法,如此下去,直到得到确定的结果或者达到了搜索深度的限制。当达到了搜索深度限制,此时无法判断结局如何,一般都是根据当前局面的形式,给出一个得分,计算得分的方法被称为评价函数,不同游戏的评价函数差别很大,需要很好的设计。
在搜索树中,表示A走棋的节点即为极大节点,表示B走棋的节点为极小节点。
在五子棋算法中,假设每一步有
递归遍历这颗博弈树的时候,
- 我们将电脑走棋的层称为MAX层,这一层要保证电脑利益的最大化,所以要选择得分最大的节点
- 我们将玩家走棋的层称为MIN层,这一层要保证玩家利益的最大化,所以要选择得分最小的节点
这就是极大极小值搜索算法的基本概念
下面是一张来自维基百科的示例图
在这里我讲一下我的评估函数:
首先我定义了一个一个列表,存储若干个元组,里面包括分值,以及棋型形状
shape_score = [(50, (0, 1, 1, 0, 0)),
(50, (0, 0, 1, 1, 0)),
(200, (1, 1, 0, 1, 0)),
(500, (0, 0, 1, 1, 1)),
(500, (1, 1, 1, 0, 0)),
(5000, (0, 1, 1, 1, 0)),
(5000, (0, 1, 0, 1, 1, 0)),
(5000, (0, 1, 1, 0, 1, 0)),
(5000, (1, 1, 1, 0, 1)),
(5000, (1, 1, 0, 1, 1)),
(5000, (1, 0, 1, 1, 1)),
(5000, (1, 1, 1, 1, 0)),
(5000, (0, 1, 1, 1, 1)),
(50000, (0, 1, 1, 1, 1, 0)),
(99999999, (1, 1, 1, 1, 1))]然后是计算单方向分值的功能函数calcScore() ,传入的参数有落子坐标、方向、电脑和玩家的棋子列表,以及已经得到的所有得分形状列表
- 首先通过循环,判断给定方向该点是否已经有得分形状了,避免重复计算,如果存在,则直接返回
0 - 然后在落子点,左右方向上循环查找得分形状,具体操作是构造坐标列表,然后与之前的
shape_score中的形状元组进行对比,如果分值大于之前的得分,则将其保存到最大得分形状列表中,同时存储到已经得到的所有得分形状列表中(只取最大的得分项) - 在最后我们还需要计算是否存在两种形状相交的情况,如果存在相交,得分为两种形状的和值
- 最后返回加分项与形状得分的和
代码如下
def calcScore(m, n, directionX, directionY, rivalList, selfList, allScoreList):
add_score = 0
max_score_shape = (0, None)
for item in allScoreList:
for pt in item[1]:
if m == pt[0] and n == pt[1] and directionX == item[2][0] and directionY == item[2][1]:
return 0
for offset in range(-5, 1):
pos = []
for i in range(0, 6):
if (m + (i + offset) * directionX, n + (i + offset) * directionY) in rivalList:
pos.append(2)
elif (m + (i + offset) * directionX, n + (i + offset) * directionY) in selfList:
pos.append(1)
else:
pos.append(0)
tmp_shap5 = (pos[0], pos[1], pos[2], pos[3], pos[4])
tmp_shap6 = (pos[0], pos[1], pos[2], pos[3], pos[4], pos[5])
for (score, shape) in shape_score:
if tmp_shap5 == shape or tmp_shap6 == shape:
if score > max_score_shape[0]:
max_score_shape = (score, ((m + (0 + offset) * directionX, n + (0 + offset) * directionY),
(m + (1 + offset) * directionX, n + (1 + offset) * directionY),
(m + (2 + offset) * directionX, n + (2 + offset) * directionY),
(m + (3 + offset) * directionX, n + (3 + offset) * directionY),
(m + (4 + offset) * directionX, n + (4 + offset) * directionY)),
(directionX, directionY))
if max_score_shape[1] is not None:
for item in allScoreList:
for pt1 in item[1]:
for pt2 in max_score_shape[1]:
if pt1 == pt2 and max_score_shape[0] > 10 and item[0] > 10:
add_score += item[0] + max_score_shape[0]
allScoreList.append(max_score_shape)
return add_score + max_score_shape[0]有了这些辅助函数,我们接下来看主评估函数evaluation()
- 首先是一个判断程序,判断这一层是否是电脑,如果是,则把它的棋子列表拷贝到
self_list,将玩家的棋子列表拷贝到rival_list,如果不是,则进行相反的操作 - 然后开始循环计算得分(包括四个方向),首先计算
self_list的得分,也就是这层主角自己的得分(这里描述可能不恰当),然后计算rival_list,也就是这层对手的得分。 - 最后返回自己的得分减去对手的得分乘以攻击系数
实现代码如下
def evaluation(is_ai):
total_score = 0
if is_ai:
self_list = listCPU
rival_list = listSelf
else:
self_list = listSelf
rival_list = listCPU
# 算自己的得分
score_all_arr = []
my_score = 0
for pt in self_list:
m = pt[0]
n = pt[1]
my_score += calcScore(m, n, 0, 1, rival_list, self_list, score_all_arr)
my_score += calcScore(m, n, 1, 0, rival_list, self_list, score_all_arr)
my_score += calcScore(m, n, 1, 1, rival_list, self_list, score_all_arr)
my_score += calcScore(m, n, -1, 1, rival_list, self_list, score_all_arr)
# 算敌人的得分, 并减去
score_all_arr_enemy = []
enemy_score = 0
for pt in rival_list:
m = pt[0]
n = pt[1]
enemy_score += calcScore(m, n, 0, 1, self_list, rival_list, score_all_arr_enemy)
enemy_score += calcScore(m, n, 1, 0, self_list, rival_list, score_all_arr_enemy)
enemy_score += calcScore(m, n, 1, 1, self_list, rival_list, score_all_arr_enemy)
enemy_score += calcScore(m, n, -1, 1, self_list, rival_list, score_all_arr_enemy)
total_score = my_score - enemy_score * ATK_RATIO
return total_score如果我们使用极大极小值搜索算法,一般情况下,我们肯定是要编写两段代码分别来计算最小,最大的分值,而通过Minimax算法延伸出来的Negamax算法可以实现只用一部分代码,既处理极大节点也处理极小节点,这就是之前的评估函数为什么要传入is_computer参数
Negamax的核心:父节点的值是各子节点的值的负数的极大值
在这里我的评估函数是根据当前搜索节点来给出分数的,每个人都会选最大的分数,然后返回到上一层节点时,会给出分数的相反数,负极大值算法,主要是代码量上的减少,时间和空间复杂度并没有什么变化
下面是维基百科上该算法的动画演示
此算法主要用于裁剪搜索树中不需要搜索的树枝,以提高运算速度,降低时间复杂度,它的基本原理是:
- 当一个MIN节点的
$\beta$ 值$\le$ 任何一个父节点的$\alpha$ 值时,剪掉该节点的所有子节点 - 当一个MAX节点的
$\alpha$ 值$\ge$ 任何一个父节点的$\beta$ 值时,剪掉该节点的所有子节点
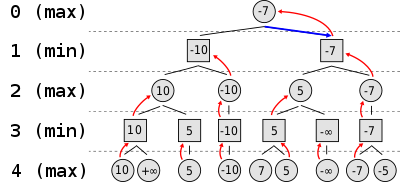
下面是来自维基百科的一张示例图
关于alpha-beta剪枝算法的具体解释,可以自行上网搜索,也可以点击下面的链接查看
http://web.cs.ucla.edu/~rosen/161/notes/alphabeta.html
下面我介绍我的主算法函数abnAlgo,这里需要传入搜索深度,alpha的值(初始时为负无穷大),beta的值(初始时为无穷大),最后是当前层是否是电脑方
- 在开始的时候,我们要定义一个递归边界,判断游戏是否结束,当搜索深度为零时或棋盘中有五子连线,直接返回调用评估函数
evaluation()- 然后我们需要得到一个包含棋盘中所有未填子坐标的列表
blank_list,这里用到了集合的差集,然后对blank_list进行搜索顺序排序,提高剪枝的效率 - 然后我们遍历
blank_list中每一个候选步,如果要评估的候选步没有相邻的棋子,则不去评估,以此减少计算
- 然后我们需要得到一个包含棋盘中所有未填子坐标的列表
- 如果当前层是电脑方,则将该候选步加入到电脑棋子列表(棋子列表都被定义为全局变量),反之则加入到玩家方棋子列表,同时加入到所有已填子列表。
- 递归调用主算法函数
abnAlgo,这里的搜索深度减1,参数alpha为负beta,参数beta为负alpha,当前层更改为当前层的对手层,将该函数返回的值的负值保存到变量value - 递归结束后,将之前加入的候选步移除
- 如果
value大于函数参数的alpha值(初始时为负无穷大),则继续判断当前深度是否已经达到自己定义的全局变量搜索深度,如果条件成立,则将最优落子点坐标赋值为候选步坐标,如果value大于等于函数参数beta值(初始时为无穷大),则直接返回beta,进行剪枝操作,在这个判断的最后,要将value的值赋给alpha - 程序的最后返回
alpha的值
下面是具体的实现代码
def abnAlgo(depth, alpha_value, beta_value, is_computer):
if checkWin(listCPU) or checkWin(listSelf) or depth == 0:
return evaluation(is_computer)
blank_list = list(set(tableListAll).difference(set(listAll)))
order(listAll, blank_list)
for step in blank_list:
global seek_count
seek_count += 1
if not has_neighbor(step, listAll):
continue
if is_computer:
listCPU.append(step)
else:
listSelf.append(step)
listAll.append(step)
value = -abnAlgo(depth - 1, -beta_value, -alpha_value, not is_computer)
if is_computer:
listCPU.remove(step)
else:
listSelf.remove(step)
listAll.remove(step)
if value > alpha_value:
if depth == DEPTH:
perfectNext[0] = step[0]
perfectNext[1] = step[1]
if value >= beta_value:
global cut_count
cut_count += 1
return beta_value
alpha_value = value
return alpha_value我在这里使用的数据结构过于简单,而忽略了计算效率,所以4层的计算,通常需要超过1分钟的搜索时间,太费时间了,后面会考虑优化数据结构,缩短搜索时间
然后在搜索的时候,没有使用提高计算效率的数据共享方式,所以在运算时经常出现浪费系统资源,数据结构混乱的情况,有时,因为界面层渲染的原因会导致出现比较严重的bug
这里优化的想法是,先从上一步落子点的周围开始搜索,快速找到最大值和最小值,从而加快剪枝的速度。
没有添加算杀模块
所谓算杀就是计算出杀棋,杀棋就是指一方通过连续的活三和冲四进行进攻,一直到赢的一种走法。我们一般会把算杀分为连续冲四胜和连续活三胜
多。一般在算杀的时候,我们优先进行连续冲三胜计算,没有找到结果的时候再进行连续冲四胜,因为算杀的情况下,每个节点只计算活三和冲四的子节点。所
以可能同样的时间,搜索只能进行4层,而算杀很多时候可以进行到12层以上。
为了方便,我们把前面的讲到全面的极大极小值搜索简称为搜索
而且很容易想到,算杀其实也是一种极大极小值搜索,具体的策略是这样的:
- MAX层,只搜索己方的活三和冲四节点,只要有一个子节点的能赢即可
- MIN 层,搜索所有的己方和对面的活三和冲四节点(进攻也是防守),只要有一个子节点能保持不败即可。
这里可能需要牵涉到机器学习深度学习方面的内容了,通过编写一些训练程序,使用机器学习库神经网络库(比如TensorFlow、PyTorch、Keras),调用GPU算力,训练生成AI模型,从而提高电脑AI的棋力,不过,这都是后话了,如果对这些感兴趣的话,可以自行查阅资料学习
我这个五子棋算法终究只是对经典算法的应用与结合,对于一般的不怎么下五子棋的玩家,电脑算法可以比较轻松的战胜玩家,但对于棋艺较高的玩家,这种程序在搜索层数的不高情况下,是无法下赢玩家的。我自己在测试的时候可以做到80%的胜率(我个人五子棋棋艺还算是比较高的),如果想要实现更深层次的算法,可以从上一点的学习模块入手,或参考我下面的给出的链接6
我的算法代码很多都是借鉴参考以下开源程序的,非常感谢,通过它们的代码让我学习到了很多
1.javascript gobang AI,五子棋AI设计教程: lihongxun945/myblog#11
2.A Gobang game implemented with C++ and SDL: https://github.com/tjumyk/Five_SDL
3.pygame做一个简单的五子棋游戏: https://blog.csdn.net/zhangenter/article/details/89078434
4.基于博弈树α-β剪枝搜索的五子棋AI: https://github.com/colingogogo/gobang_AI
5.Gobang game with artificial intelligence in 900 Lines !!: https://github.com/skywind3000/gobang
6.An implementation of the AlphaZero algorithm for Gomoku (also called Gobang or Five in a Row)https://github.com/junxiaosong/AlphaZero_Gomoku
如果有任何关于代码的疑问,可以通过:e-mail:[email protected]联系我