Esta aplicação -- desenvolvida na disciplina Algoritmos e Estruturas de Dados do Mestrado (PPGCC - UFJF) -- conta com uma estrutura de dados do tipo árvore Patricia (Patricia tree ou Radix tree) para realizar operações no banco de dados USDA (United States Department of Agriculture).
-
A estrutura, criada como um IMDB (In-Memory Database), permite:
- a definição de campos e inserção de valores (i.e., inserção de chaves primárias)
- busca
- remoção
- a instanciação de tabelas
- contar registros (como SELECT COUNT FROM e SELECT COUNT FROM WHERE)
- consultas JOIN (como INNER JOIN, LEFT OUTER JOIN, RIGHT OUTER JOIN e FULL OUTER JOIN)
-
Este tipo de estrutura foi escolhido por ser útil no tratamento de chaves de tamanho variável, podendo estas serem extremamente longas, como títulos e frases.
-
Em um segundo momento, buscando um aprimoramento da solução (e.g., operações mais rápidas e menos custosas em termo de espaço) a árvore Patricia foi transformada em uma tabela hash de árvores Patricia.
- Java
Tries, também conhecidas como árvores digitais ou árvores de prefixos, são tipos de árvores de busca utilizadas para implementar tabelas de símbolos cujas chaves são strings[1].
Em uma trie, por ser uma árvore n-ária, uma chave é recursivamente comparada a um nó da árvore até chegar ao nó procurado ou não o encontrar.
A árvore Patricia (Practical Algorithm to Retrieve Information Coded in Alphanumeric) deriva da estrutura trie, porém diferencia-se desta no aspecto de que os nós que possuem apenas um filho são agrupados -- o que reduz o gasto de memória.
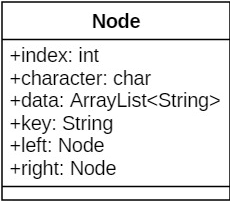
Faz-se a separação entre nós pais e nós folhas, onde os nós pais são representados por instâncias da classe Node (figura abaixo) cujos atributos data e key são nulos, enquanto que nas folhas, os atributos nulos são o index e o character.
 |
|---|
| Representação da classe Node |
É feita comparando-se alfanumericamente as Strings correspondentes às chaves primárias, que são armazenadas sempre como nós folhas.
O processo de inserção começa pela raiz e segue-se segundo descrito abaixo:
1. Caso a raiz seja um registro, compara-se a chave correspondente a este registro com a chave do registro que se queira inserir.
2. Cria-se um novo nó com a primeira posição na qual as Strings divergem e com o caractere presente nesta posição no nó raiz. Este novo nó passa a ser a raiz da árvore
3. Dentre os dois registros (o que se quer inserir e a raiz), o que possuir o caractere especificado pelo nó raiz, na posição especificada por este, passa a ser o filho esquerdo, enquanto que o outro passa a ser o filho direito.
4. Repete-se recursivamente, resultando em uma árvore binária onde todos os nós têm dois filhos.
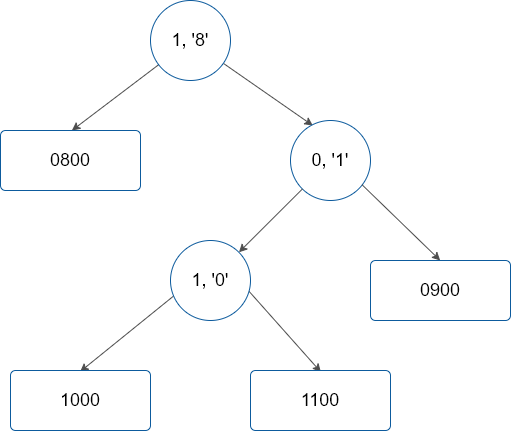
A figura a seguir traz uma representação da árvore Patrícia.
 |
|---|
| Representação da árvore Patricia com as chaves 0800, 0900, 1000 e 1100 armazenadas |
Pela literatura, sabe-se que o número médio de comparações a serem feitas nessa árvore é log(N), onde N é o número de registros.
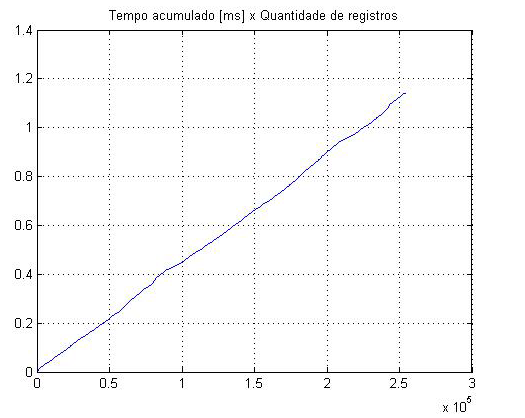
Porém como os registros se apresentam (no arquivo de dump) ordenados alfabeticamente, espera-se que as operações realizadas na árvore tendam ao pior caso, que seria da ordem N (como se pode ver expressado no gráfico abaixo).
 |
|---|
| Inserção de todos os registros na tabela nut_data |
Baseia-se na comparação da chave que se quer buscar com a raiz da árvore.
1. Considerando que a árvore possua mais que um registro, e, portanto, a raiz não é um registro, compara-se o caractere presente na raiz com com o caractere presente na chave na posição indicada pela raiz.
2. Caso a comparação seja positiva, segue-se para a esquerda e repete-se o procedimento.
3. Caso contrário, segue-se para a direita recursivamente.
4. A recursão pára ao se atingir o nó folha correspondete à chave procurada.
5. Caso não a ache, o retorno é nulo.
A remoção de qualquer registro na árvore segue os seguintes passos:
1. Remove-se o registro
2. Remove-se o pai do registro
3. O irmão do registro passa a ser o pai
Os passos acima descritos valem para se remover qualquer nó folha, não importando se este é filho esquerdo ou direito ou a altura em que este se encontra na árvore.
-
Fez-se um método para contar todos os registros de uma tabela, dado o nome da tabela. Este método considera apenas registros que foram indexados a partir de suas chaves primárias.
-
Dado o nome da tabela, o nome do campo e o valor que este deve apresentar, criou-se um método que retorna a quantidade de campos iguais presentes em uma tabela.
A cláusula JOIN combina campos de tabelas diferentes e os transforma em um novo conjunto.
Considere duas tabelas (assinaladas por 1 e 2), onde 1 é a tabela da esquerda e a 2 da direita.
-
O INNER JOIN é feito percorrendo-se os registros da tabela 1 e procurando se as chaves correspondentes a tais registros se fazem presentes na tabela 1.
-
O percurso na primeira árvore apresenta complexidade O(N).
-
A busca na segunda árvore, considerando o pior caso, também apresenta complexidade O(N).
-
Portanto, podemos concluir que a complexidade do método INNER JOIN tende a N2.
-
O LEFT JOIN, assim como o INNER JOIN, representa a interseção entre as tabelas 1 e 2 por um campo considerado chave primária.
-
Entretanto, o LEFT JOIN não representa somente a interseção entre os conjuntos, mas também todos os outros camposda tabela 1 que não apresentam correspondência na tabela 2.
-
O Right Join se parece com o Left Join, entretanto, considera-se campos não nulos na segunda tabela e se pode considerar campos nulos na primeira.
-
Logo é o contrário do Left Join, tendo seu conjunto resultante representado pelo conjunto da tabela 2.
- O Full Join pode ser visto como a uni~ao entre os Joins Left e Right, podendo ser representado pela união das tabelas 1 e 2.
-
Com o objetivo de se obter buscas mais rápidas, propôs-se a implementação de uma modificação na estrutura original.
-
Tal modificação se dá pela implementação de uma tabela hash, cujo acesso, no melhor caso, é direto.
-
A tabela é formada por um vetor de árvores Patrícia. Portanto, trata-se da abordagem de tabela hash com encadeamento externo.
-
Para uma tabela de tamanho m, cuja função de hash apresenta uma distribuição uniforme, o custo para acessar uma posição na tabela é 1/m. Logo, 1/m é o custo para se buscar uma árvore na tabela.
-
Considerando o pior caso da árvore, o custo para se buscar um registro na árvore é O(N). Portanto, pode-se dizer que a complexidade de busca na tabela hash de árvores tende a N/m.
-
Para a implementação da estrutura, escolheu-se m = 1051. É valido notar que a escolha por um número primo é uma tentativa de se minimizar colisões.
-
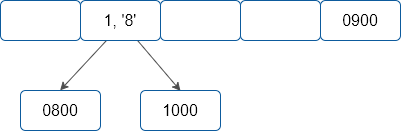
A valor de demonstração, o passo a passo seguinte elucida o processo de inserção de registros na estrutura, considerando um tamanho hipotético de m = 5.
-
Considere ainda, hipoteticamente, que as chaves 0800, 0900, 1000 e 1100 quando aplicadas à função de hash apresentem os seguintes valores, respectivamente: 1, 4, 1, 1.
 |
|---|
| Primeiro passo da inserção |
 |
|---|
| Segundo passo da inserção |
 |
|---|
| Terceiro passo da inserção |
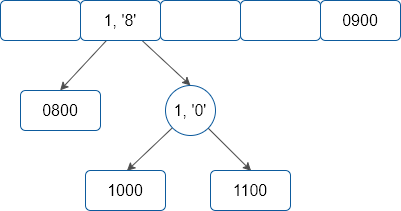 |
|---|
| Quarto passo da inserção |
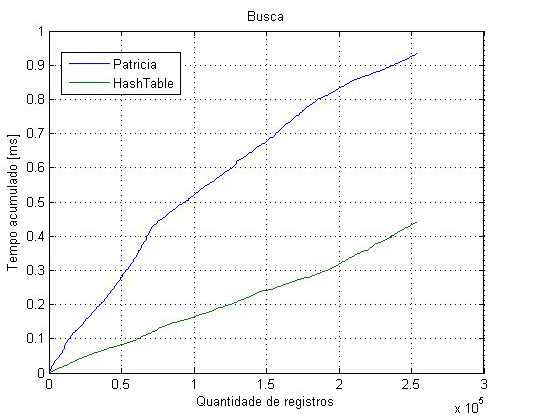
A figura abaixo apresenta uma comparação entre o tempo acumulado de busca por quantidade de registro considerando-se as duas estruturas.
 |
|---|
| Busca de todos os registros da tabela nut_data |
Percebe-se que a curva referente à estrutura modificada (tabela hash de árvores) cresce mais lentamente que a apresentada pela árvore Patricia. Logo, há um decréscimo no tempo de busca.
As demais operações apresentaram comportamento semelhante à busca.