-
Notifications
You must be signed in to change notification settings - Fork 0
Gridfour Raster Index and Coordinate Systems
This wiki page describes the integer indexing and real-valued coordinate systems used in the Gridfour software library. The approach described below is used both for the Gridfour Virtual Raster Store (GVRS) API and for all other modules in the Gridfour system.
For applications that do not require geometry-based operations, a raster data set can be viewed as a simple two-dimensional array. In such cases, the data contained in the raster product can be accessed using integer indices. The figure below illustrates a typical layout of a non-spatial data grid. The variable i is used to indicate row and j to indicate column. Variables zi,j give the values for each data cell. For reasons of software efficiency, the Gridfour library often uses arrays of one-dimension rather than two. In one-dimensional arrays, the data is organized in row-major order. The small numbers in the upper-left corner of each data cell in the figure represent the order of elements within the raster grid. They correspond to the integer indices for array elements when the grid is stored in a one-dimensional array. This ordering scheme is also used when data is serialized for storage or transmission between applications.
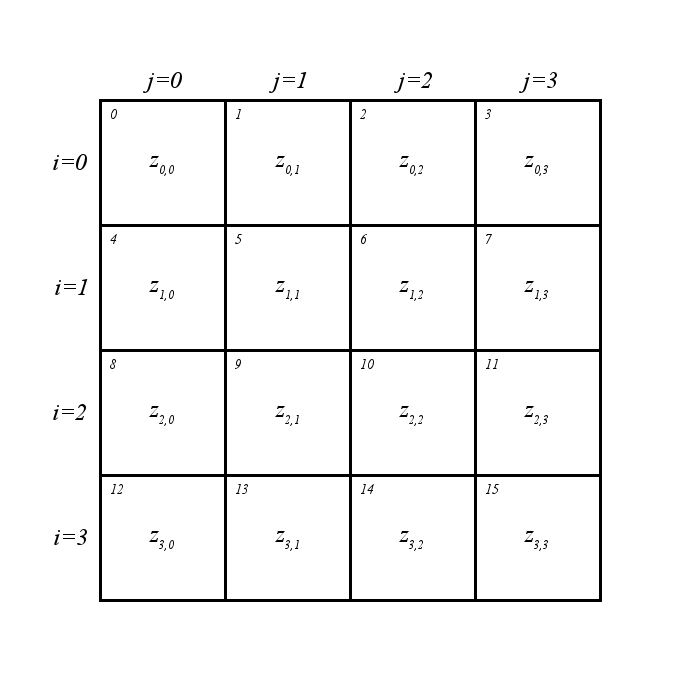
Many applications apply a spatial interpretation to raster data sets. In such cases, we extend the variables i and j to real-valued counterparts, i′ and j′. These coordinates, which we refer to as "grid coordinates", allow us to indicate any point within the raster grid using unitless, real-valued coordinates based on row and column. Gridfour also allows applications to tie real-world coordinates (Cartesian coordinates, geographic coordinates, etc.) to the grid. To do so, an "anchor point" designated (x0, y0) is attached to the center of the cell in the first row and first column of the grid. Cells are treated as having a uniform width, w, and height, h.
The figure below shows an example of the assignments of coordinates to a raster product with a spatial basis.

The figure above shows points at the center of each raster cell. The Gridfour software library often (but not always) assumes that the data in a raster product with a spatial basis represents a continuous surface. The data values are treated as being tied to points located at the center of each grid cell. These points are assigned integral coordinates. Points falling between data samples are assigned non-integral coordinates.
The center-point interpretation of data values is useful for interpolation, data-smoothing, digital filtering, and other applications that perform operations over a continuous surface.
The Gridfour Virtual Raster Store (GVRS) API supports two broad categories of real-valued coordinate systems:
- Grid Coordinates are the row and column specifications i′ and j′ that were described above. Grid coordinates are used to perform lookup operations on raster data sets, and are also applied to interpolation operations.
- Model Coordinates are real-valued coordinates computed using information about the cell-size and anchor position described above. Currently, Gridfour supports two subcategories for model coordinates: Cartesian (x, y) and geographic coordinates (latitude and longitude). Additional kinds of model coordinates (including polar and complex coordinates) may be considered in the future.
Internally, the GVRS API uses specifications about the anchor point and cell sizes to establish affine transforms for mapping model coordinates to grid coordinates. The API also allows applications to specify custom affine transforms to support operations such as rotations, skewed axes, or reflections.
The following examples illustrate the way the Gridfour API uses integer indices and real-valued grid and model coordinates.
As an example of the way a raster-query operation might occur, consider the following steps:
- The application specifies a pair of model coordinates, (x, y).
- An API transforms the model coordinates to grid coordinates (i′, j′) using an appropriate affine transform.
- The API performs a round-off operation to convert the grid coordinates to integer row and column indices (i, j).
- If the data is stored in a one-dimensional array, the array index is computed as index = i*nColumnsInGrid+j.
From the discussion above, we can express model coordinates (x, y) in terms of i′ and j′ using the following
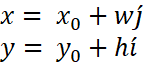
Solving for i′ and j′, we find grid coordinates
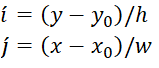
And finding the integer indices for row and column is simply a matter of round-off.
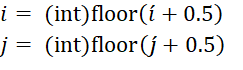
This computation is straightforward, but it has one complication. In the 4-by-4 grid shown in the figures above, the coordinates (i′, j′) for the point in the lower-right corner are (3.5, 3.5). When we convert them to integer indices, their values round up to 4. Since Gridfour starts the indices for rows and columns at zero, the computed indices for the corner point would be out-of-range. As shown in the picture above, there is no value z4,4.
To compensate for this numeric precision and round-off issues at the fringes of the data set, the Gridfour coordinate-to-index conversion methods (the "mapping" methods) apply logic to truncate values lying on the edges of the raster.
One of the motivations for treating the values in a raster as point samples is to support interpolation. The example below shows an example of a simple bilinear interpolation operating over the grid coordinate system.
We wish to interpolate a value z for a point positioned somewhere between four sample points on the grid. The position of the interpolation point is given by the grid coordinates (i′, j′). The result will be a linear combination of the values zi,j, zi,j+1, zi+1,j, and zi+1,j+1. The geometry for the interpolation is illustrated below.
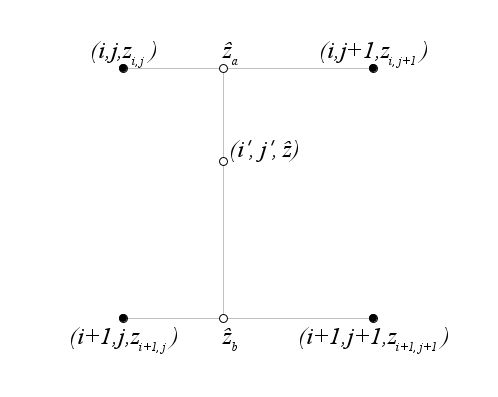
The indexing of points for interpolation is different from that used for the raster look-up operation. For interpolation, we do not round off the grid coordinates, but instead truncate their values to find the first corner in a set of 4 points taken from the overall raster.
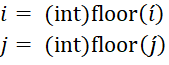
We can find two parameters s and t in the range zero to one using
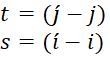
And the interpolated value can be computed using those parameters as shown
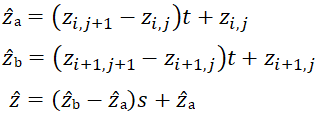
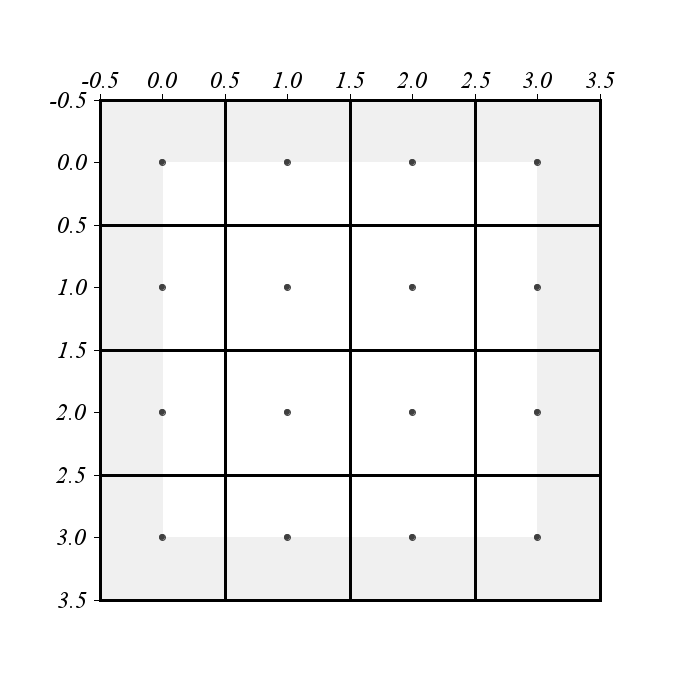
Interpolation techniques are only effective in regions that are bracketed by sample data values. As shown in the figure below, one consequence of the way Gridfour defines its coordinate systems is that the interpolated region is limited to a sub-domain of the overall raster bounds. In cases where an application requires values for points in the "fringe area" (shown in gray), the Gridfour API generally constrains the out-of-bounds coordinates to the limits of the interpolation region. Even if a point lies in a row that is in fringe area, it might still be possible to interpolate values based on colummn... and vice versa. However, in cases where a coordinate of interest lies entirely outside the domain of the raster (i.e. it is beyond the fringe), the Gridfour interpolators generally treat the value as undefined (typicaly as a floating point not-a-number value).
There are other ways of specifying coordinate systems for rasters. For simplicity, Gridfour sticks to the system described above. In most cases, it is possible to specify a model coordinate system for Gridfour raster that is compatible with other data products.
In designing the Gridfour API's we have tried to follow a consistent and predictable approach. The information supplied in this wiki article should help clarify that goal.