#FUNPSY (FUNctional magnetic resonance imaging Phase SYnchronization)
A simple collection of Matlab routines to
- convert BOLD time series into phase time series after band-pass filtering and Hilbert transform
- compute instantaneous intersubject phase synchronization (an instantaneous measure of similarity between a group of subjects undergoing same stimulation)
- compute instantaneous dynamic functional connectivity consistent across subjects undergoing same stimulation
Please see: Glerean, E., Salmi, J., Lahnakoski, J.M., Jääskeläinen, I.P., Sams, M. (2012). Functional Magnetic Resonance Imaging Phase Synchronization as a Measure of Dynamic Functional Connectivity. Brain connectivity 2(2): 91-101. doi:10.1089/brain.2011.0068
See example of the tool in action in these papers:
- Nummenmaa L., Smirnov D., Lahnakoski J., Glerean E., Jääskeläinen I.P., Sams M., Hari R. (2013) Mental Action Simulation Synchronizes Action-Observation Circuits Across Individuals. Journal of Neuroscience doi:10.1523/JNEUROSCI.0352-13.2014 http://www.jneurosci.org/content/34/3/748.full
- Nummenmaa L., Saarimäki H.; Glerean E.; Gotsopoulos A.; Jääskeläinen I.P.; Hari R.; Sams M. (2014) Emotional Speech Synchronizes Brains Across Listeners And Engages Large-Scale Dynamic Brain Networks. Neuroimage doi:10.1016/j.neuroimage.2014.07.063 http://www.sciencedirect.com/science/article/pii/S1053811914006466
Typo: the frequency band in Nummenmaa 2014 JNeurosci is written as 0.30–0.95 Hz while it should have been 0.030–0.095 Hz.
The documentation present on this page is minimal. The toolbox does not provide a graphical interface. The best way to learn how to use it is to read the code and comments in funpsy_demo.m and re-run same commands with your own data.
The code is managed with GIT and can be downloaded at https://github.com/eglerean/funpsy . To download it, open a terminal and type
git clone https://github.com/eglerean/funpsy
Then make sure your matlab path sees the funpsy folder and its subfolders.
Please make sure you also have the NIFTI tools for matlab installed: http://www.mathworks.com/matlabcentral/fileexchange/8797-tools-for-nifti-and-analyze-image
Funpsy currently works with data from experiments were all subjects are undergoing the same stimulation in sync (e.g. watching a feature film). It is an extension of methods such as intersubject correlation (https://code.google.com/p/isc-toolbox/) with the added temporal dimension. The phase synchrony method has however also been used successfully at rest with real data and models (see for example http://journals.plos.org/ploscompbiol/article?id=10.1371/journal.pcbi.1004100).
The toolbox has been tested with data preprocessed following the FEAT FSL pipeline with coregistration to the 2mm MNI 152 template. Other spatial resolutions or volume sizes are allowed as long as the user provides a matching mask of voxels of interests of the same size of the data.
The easiest way is for you to open funpsy_demo.m and look at the comments. Just run funpsy_demo with your dataset and parameters of choice to obtain all the results. At the moment the demo uses the AAL atlas as set of ROIs, but it is possible to generate your own rois.
The following three measures are computed:
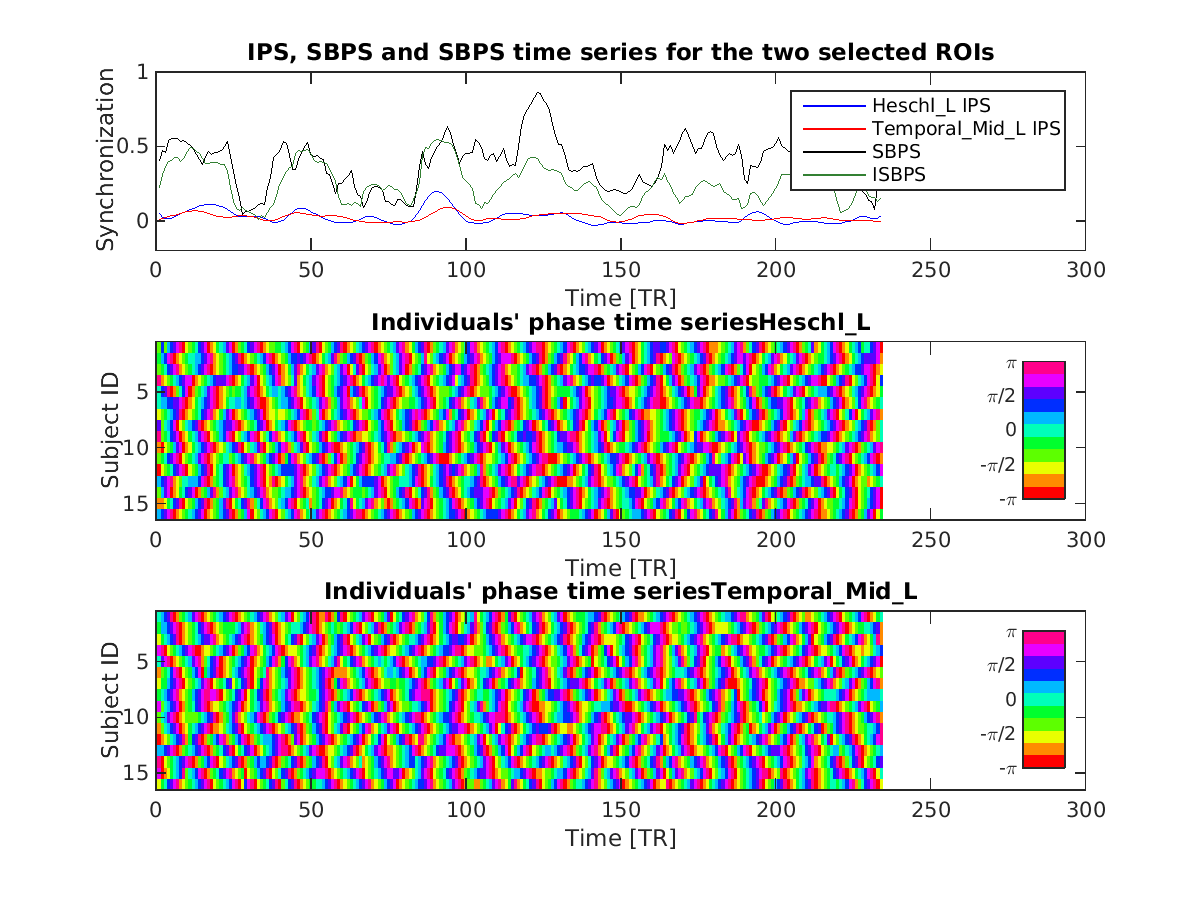
- Intersubject Phase Synchronization (IPS): a single voxel measure of time-varying synchronization across subjects (massive univariate approach)
- Seed Based Phase Synchronization (SBPS): a bi-variate measure of time-varying synchronization (i.e. a measure of dynamic functional connectivity at group level).
- Intersubject Seed Based Phase Synchronization (ISBPS): similar to the previous one, but with the added constraint that also each seed has to be synchronous across subjects (still at an experimental stage since it is not straightforward to compare this to other correlation based methods)
The script funpsy_example.m will generate some visualization after all IPS/SBPS/ISBPS time series are computed.
Move and extend the documentation present at funpsy_demo.m into the subsections below.
Currently the toolbox uses an optimal FIR filter. Remember to specify the right TR as this is important for the filter design. If you are trying a different filter, it is recommended that you test the design separately. Code for doing this will be added here.
funpsy_ips
funpsy_sbps
funpsy_isbps
funpsy_makerois
A) IPS: results are stored in the subfolder 'results' of the specified output folder. The IPS is stored in ips.mat which is a 4D matrix with first three dimension equal to the x, y, z dimensions of the subjects. Fourth dimension is time (number of time points). Each voxel stores values of synchronization (between -1 and 1).
B) SBPS: results are stored in subfolder 'results/sbps'. Files are named as numbers equivalent to the ROI id. File 1.mat will contain all the link time-series from ROI 1 to all other N-1 rois (i.e. a total of N-1 connectivity time-series). File 2.mat will contain N-2 link time series (from roi 2 to roi 3, 4, ..., N). The time series of connectivity between 1 and 2 is already stored in 1.mat hence it is not stored in 2.mat.
C) ISBPS: see SBPS, subfolder is 'results/isbps'
There are three ways of computing stats: A) data driven approach B) model based approach C) comparing groups (permutation based two sample ttest)
Case A: this means that you just want to see which voxels (for IPS) or links (for SBSP) are in sync across subjects and also when they are in sync. The current script funpsy_stats.m does that (although ISBPS is not there yet as noted by one of you). From personal experience, the uncorrected p values that are obtained by permutations are very similar to a parametric Rayleigh test http://www.neurophys.wisc.edu/comp/docs/not011/not011.html (scroll down to see the table where n - first column - is the number of subjects). For the multiple comparisons problem see next subsection. At the moment the stats script is not optimized for those cases with small amount of RAM or small amount of CPUs. Personal notes: I personally find this data-driven approach a bit uninteresting: we have used it as a first starting point to show which areas are on average in sync across subjects (for this also the ISCtoolbox is good https://code.google.com/p/isc-toolbox/), but the interesting statistics are in the model driven case (case B). Finding that at some time points, some areas are in sync across subjects, might easily lead to the dangers of reverse inference (you find that the FFA is significantly in sync in one time point and most likely there will be a face in the stimulus at that moment, but this does not test for all the faces across the whole experiment; see also http://www.sciencedirect.com/science/article/pii/S1364661305003360). Model based approach better tests this hypothesis.
Case B: for the model based approach (used for example in the papers linked above), we obtain time series of intersubject synchrony for each voxel (IPS case) or for each link (SBPS and ISBPS cases). Then these time series are compared against a model, i.e. another time series that could represent annotations from the movie (Lahnakoski 2012 Plos One), valence or arousal (Nummenmaa 2012 PNAS, Nummenmaa 2014 Neuroimage) or some experimental conditions (Nummenmaa 2014 J Neurosci). I.e., the toolbox is only needed to generate group level phase synchrony time series. These time series are then tested against a model like you would do in a normal GLM with only one hypothetical subject who has synchronization values rather than BOLD signal). This means that (for the IPS case) you can use other packages (FSL or SPM) to perform GLM analysis. For the connectivity case there's no real package that tests for link time series vs a model. A function funpsy_glm.m will do this.
Case C: similar to case B but here we want to compare groups (e.g. controls vs drug). This is under development and paper not yet submitted. Code will be available later.
Multiple comparisons are happening in space (many voxels or links tested) and -only for case A- also in time. Case B and C are getting rid of time (ie glm results will produce a map of voxels whose synchrony covaries with the model). For case A: Funpsy_stats provides spatial FDR correction based on an approach similar to the max statistics (Nichols 2002) but it doesn't take in consideration the number of time points. Ideally, one would have to divide the desired p value threshold by the number of time points. In reality, the synchronisation time series are autocorrelatied, i.e. it is enough to divide by the estimated number of independent time points (degrees of freedom) which is smaller than the total number of time points. One can estimate this parametrically (see appendix B of our paper Alluri 2012 Neuroimage). A function that does this for you is here in our lab's repository: https://git.becs.aalto.fi/bml/bramila/blob/master/bramila_autocorr.m).
Personal comment: You now see why I find case A (data driven approach) least interesting since just the temporal length of the data is going to affect the statistical threshold. Instead of a frequentist approach, a Bayesian solution might be better suited for case A (anyone wants to implement the Bayesian approach with STAN http://mc-stan.org/? bear in mind that you need a computational cluster to do this since from our tests the Bayesian way is much slower computationally).
Case B and C don't have the multiple comparison problem in time as they get rid of the temporal dimension. You need however to correct for multiple comparisons spatially. You can feed your p values to the Benjamin hochberg FDR function (see matlab mafdr). This is a bit strict since it doesn't take into account spatial autocorrelation (I.e. The number of independent comparisons is smaller than the number of tested voxels). Cluster correcting the results is a better option. I am planning to add a permutation based cluster correction approach, but it's not a priority at the moment. If you run your glm with standard packages (fsl, spm etc) you can use what is provided there.
A different story is for the network approach. For this case you can use the network based statistics https://sites.google.com/site/bctnet/comparison/nbs however I found it a bit too lenient when the number of nodes (and links) increases (i.e. it seems that it is always able to find a large connected component when there's millions of links). In Nummenmaa 2014 Neuroimage we had a network of ~13 million links, the NBS approach was giving way too many significant links. On the other hand, the BHFDR approach becomes too strict since you need to have a p value of 10e-7 for the strongest link (almost nothing survived). In the end we used a similar approach as used in GWAS studies, with the so called positive FDR (pFDR http://www.pnas.org/content/100/16/9440.full, a somewhat Bayesian interpretation of FDR: https://projecteuclid.org/euclid.aos/1074290335). For that, we decided to set a q value of 10% rather than the usual 5% as also done in genetics. I can help on this bit if you are going to deal with dense networks with millions of links.
Code under development, paper in preparation.
Add code here
Added more atlases for connectivity analysis. Currently working on a function for group comparisons (i.e. is group A more in-synch than group B) and model based analysis (general linear model of time series of synchronization). A small "how to" has been added to wiki pages.
- SVPS: a seed-voxel approach, i.e. connectivity from a given seed to the rest of the brain. Bits of code for this are already committed but the feature is not ready yet.
- Parallel computing and optimizing permutation tests
- Add more atlases for ROIs (UCLA, CC200 and CC400)
###Future Python version of the code (send an email if you want to help!)