Skip to content

Latest commit

 

History

History
397 lines (340 loc) · 10.7 KB

README_EN.md

File metadata and controls

397 lines (340 loc) · 10.7 KB
comments difficulty edit_url rating source tags
true
Medium
1476
Weekly Contest 305 Q2
Tree
Depth-First Search
Breadth-First Search
Union Find
Graph
Array
Hash Table

2368. Reachable Nodes With Restrictions

中文文档

Description

There is an undirected tree with n nodes labeled from 0 to n - 1 and n - 1 edges.

You are given a 2D integer array edges of length n - 1 where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree. You are also given an integer array restricted which represents restricted nodes.

Return the maximum number of nodes you can reach from node 0 without visiting a restricted node.

Note that node 0 will not be a restricted node.

 

Example 1:

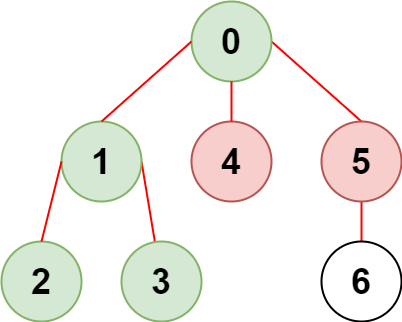
Input: n = 7, edges = [[0,1],[1,2],[3,1],[4,0],[0,5],[5,6]], restricted = [4,5]
Output: 4
Explanation: The diagram above shows the tree.
We have that [0,1,2,3] are the only nodes that can be reached from node 0 without visiting a restricted node.

Example 2:

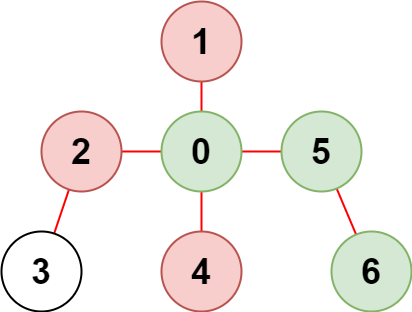
Input: n = 7, edges = [[0,1],[0,2],[0,5],[0,4],[3,2],[6,5]], restricted = [4,2,1]
Output: 3
Explanation: The diagram above shows the tree.
We have that [0,5,6] are the only nodes that can be reached from node 0 without visiting a restricted node.

 

Constraints:

  • 2 <= n <= 105
  • edges.length == n - 1
  • edges[i].length == 2
  • 0 <= ai, bi < n
  • ai != bi
  • edges represents a valid tree.
  • 1 <= restricted.length < n
  • 1 <= restricted[i] < n
  • All the values of restricted are unique.

Solutions

Solution 1: DFS

First, we construct an adjacency list $g$ based on the given edges, where $g[i]$ represents the list of nodes adjacent to node $i$. Then we define a hash table $vis$ to record the restricted nodes or nodes that have been visited, and initially add the restricted nodes to $vis$.

Next, we define a depth-first search function $dfs(i)$, which represents the number of nodes that can be reached starting from node $i$. In the $dfs(i)$ function, we first add node $i$ to $vis$, then traverse the nodes $j$ adjacent to node $i$. If $j$ is not in $vis$, we recursively call $dfs(j)$ and add the return value to the result.

Finally, we return $dfs(0)$.

The time complexity is $O(n)$, and the space complexity is $O(n)$. Where $n$ is the number of nodes.

Python3

class Solution:
    def reachableNodes(
        self, n: int, edges: List[List[int]], restricted: List[int]
    ) -> int:
        def dfs(i: int) -> int:
            vis.add(i)
            return 1 + sum(j not in vis and dfs(j) for j in g[i])

        g = defaultdict(list)
        for a, b in edges:
            g[a].append(b)
            g[b].append(a)
        vis = set(restricted)
        return dfs(0)

Java

class Solution {
    private List<Integer>[] g;
    private boolean[] vis;

    public int reachableNodes(int n, int[][] edges, int[] restricted) {
        g = new List[n];
        vis = new boolean[n];
        Arrays.setAll(g, k -> new ArrayList<>());
        for (var e : edges) {
            int a = e[0], b = e[1];
            g[a].add(b);
            g[b].add(a);
        }
        for (int i : restricted) {
            vis[i] = true;
        }
        return dfs(0);
    }

    private int dfs(int i) {
        vis[i] = true;
        int ans = 1;
        for (int j : g[i]) {
            if (!vis[j]) {
                ans += dfs(j);
            }
        }
        return ans;
    }
}

C++

class Solution {
public:
    int reachableNodes(int n, vector<vector<int>>& edges, vector<int>& restricted) {
        vector<int> g[n];
        vector<int> vis(n);
        for (auto& e : edges) {
            int a = e[0], b = e[1];
            g[a].emplace_back(b);
            g[b].emplace_back(a);
        }
        for (int i : restricted) {
            vis[i] = true;
        }
        function<int(int)> dfs = [&](int i) {
            vis[i] = true;
            int ans = 1;
            for (int j : g[i]) {
                if (!vis[j]) {
                    ans += dfs(j);
                }
            }
            return ans;
        };
        return dfs(0);
    }
};

Go

func reachableNodes(n int, edges [][]int, restricted []int) int {
	g := make([][]int, n)
	vis := make([]bool, n)
	for _, e := range edges {
		a, b := e[0], e[1]
		g[a] = append(g[a], b)
		g[b] = append(g[b], a)
	}
	for _, i := range restricted {
		vis[i] = true
	}
	var dfs func(int) int
	dfs = func(i int) (ans int) {
		vis[i] = true
		ans = 1
		for _, j := range g[i] {
			if !vis[j] {
				ans += dfs(j)
			}
		}
		return
	}
	return dfs(0)
}

TypeScript

function reachableNodes(n: number, edges: number[][], restricted: number[]): number {
    const vis: boolean[] = Array(n).fill(false);
    const g: number[][] = Array.from({ length: n }, () => []);
    for (const [a, b] of edges) {
        g[a].push(b);
        g[b].push(a);
    }
    for (const i of restricted) {
        vis[i] = true;
    }
    const dfs = (i: number): number => {
        vis[i] = true;
        let ans = 1;
        for (const j of g[i]) {
            if (!vis[j]) {
                ans += dfs(j);
            }
        }
        return ans;
    };
    return dfs(0);
}

Solution 2: BFS

Similar to Solution 1, we first construct an adjacency list $g$ based on the given edges, then define a hash table $vis$ to record the restricted nodes or nodes that have been visited, and initially add the restricted nodes to $vis$.

Next, we use breadth-first search to traverse the entire graph and count the number of reachable nodes. We define a queue $q$, initially add node $0$ to $q$, and add node $0$ to $vis$. Then we continuously take out node $i$ from $q$, accumulate the answer, and add the unvisited adjacent nodes of node $i$ to $q$ and $vis$.

After the traversal, we return the answer.

The time complexity is $O(n)$, and the space complexity is $O(n)$. Where $n$ is the number of nodes.

Python3

class Solution:
    def reachableNodes(
        self, n: int, edges: List[List[int]], restricted: List[int]
    ) -> int:
        g = defaultdict(list)
        for a, b in edges:
            g[a].append(b)
            g[b].append(a)
        vis = set(restricted + [0])
        q = deque([0])
        ans = 0
        while q:
            i = q.popleft()
            ans += 1
            for j in g[i]:
                if j not in vis:
                    q.append(j)
                    vis.add(j)
        return ans

Java

class Solution {
    public int reachableNodes(int n, int[][] edges, int[] restricted) {
        List<Integer>[] g = new List[n];
        boolean[] vis = new boolean[n];
        Arrays.setAll(g, k -> new ArrayList<>());
        for (var e : edges) {
            int a = e[0], b = e[1];
            g[a].add(b);
            g[b].add(a);
        }
        for (int v : restricted) {
            vis[v] = true;
        }
        Deque<Integer> q = new ArrayDeque<>();
        q.offer(0);
        int ans = 0;
        for (vis[0] = true; !q.isEmpty(); ++ans) {
            int i = q.pollFirst();
            for (int j : g[i]) {
                if (!vis[j]) {
                    q.offer(j);
                    vis[j] = true;
                }
            }
        }
        return ans;
    }
}

C++

class Solution {
public:
    int reachableNodes(int n, vector<vector<int>>& edges, vector<int>& restricted) {
        vector<int> g[n];
        vector<int> vis(n);
        for (auto& e : edges) {
            int a = e[0], b = e[1];
            g[a].emplace_back(b);
            g[b].emplace_back(a);
        }
        for (int i : restricted) {
            vis[i] = true;
        }
        queue<int> q{{0}};
        int ans = 0;
        for (vis[0] = true; !q.empty(); ++ans) {
            int i = q.front();
            q.pop();
            for (int j : g[i]) {
                if (!vis[j]) {
                    vis[j] = true;
                    q.push(j);
                }
            }
        }
        return ans;
    }
};

Go

func reachableNodes(n int, edges [][]int, restricted []int) (ans int) {
	g := make([][]int, n)
	vis := make([]bool, n)
	for _, e := range edges {
		a, b := e[0], e[1]
		g[a] = append(g[a], b)
		g[b] = append(g[b], a)
	}
	for _, i := range restricted {
		vis[i] = true
	}
	q := []int{0}
	for vis[0] = true; len(q) > 0; ans++ {
		i := q[0]
		q = q[1:]
		for _, j := range g[i] {
			if !vis[j] {
				vis[j] = true
				q = append(q, j)
			}
		}
	}
	return
}

TypeScript

function reachableNodes(n: number, edges: number[][], restricted: number[]): number {
    const vis: boolean[] = Array(n).fill(false);
    const g: number[][] = Array.from({ length: n }, () => []);
    for (const [a, b] of edges) {
        g[a].push(b);
        g[b].push(a);
    }
    for (const i of restricted) {
        vis[i] = true;
    }
    const q: number[] = [0];
    let ans = 0;
    for (vis[0] = true; q.length; ++ans) {
        const i = q.pop()!;
        for (const j of g[i]) {
            if (!vis[j]) {
                vis[j] = true;
                q.push(j);
            }
        }
    }
    return ans;
}