Skip to content

2D Sod

Jump to bottom Edit New page
evazlimen edited this page Jul 16, 2024 · 2 revisions

2D Sod Shock Test

Illustrates the ability of a code to resolve shocks and contact discontinuities over a narrow region. Parameters from Sod (1978). The test consists of two constant states (on left pressure and density are equal to 1; on right they are equal to 0.1) separated by a discontinuity at 0.5. Gamma is set to 1.4. This test is performed with the default hydro build (cholla/builds/make.type.hydro) and Van Leer integrator.

Parameter file: (modified from cholla/examples/2D/sod.txt)

Modified to add zl_bcnd=0 and zu_bcnd=0.

#
# Parameter File for 2D Sod Shock tube
#

################################################
# number of grid cells in the x dimension
nx=100
# number of grid cells in the y dimension
ny=100
# number of grid cells in the z dimension
nz=1
# final output time
tout=0.2
# time interval for output
outstep=0.2
# name of initial conditions
init=Riemann
# domain properties
xmin=0.0
ymin=0.0
zmin=0.0
xlen=1.0
ylen=1.0
zlen=1.0
# type of boundary conditions
xl_bcnd=3
xu_bcnd=3
yl_bcnd=3
yu_bcnd=3
zl_bcnd=0
zu_bcnd=0
# path to output directory
outdir=./

#################################################
# Parameters for 2D Riemann problems
# density of left state
rho_l=1.0
# velocity of left state
vx_l=0.0
vy_l=0.0
vz_l=0.0
# pressure of left state
P_l=1.0
# density of right state
rho_r=0.1
# velocity of right state
vx_r=0.0
vy_r=0.0
vz_r=0.0
# pressure of right state
P_r=0.1
# location of initial discontinuity
diaph=0.5
# value of gamma
gamma=1.4

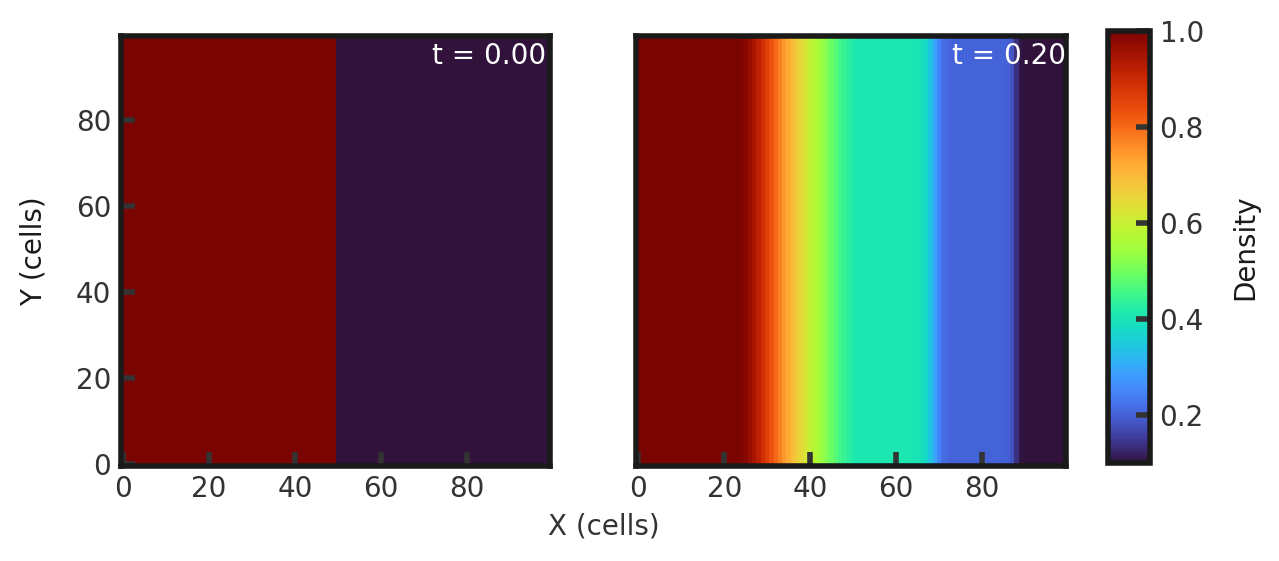
Upon completion, you should obtain two output files. The initial and final densities (in code units) of a slice along the y-midplane is shown below. Examples of how to plot projections and slices can be found in cholla/python_scripts/Projection_Slice_Tutorial.ipynb.
Two 2D histograms side by side, showing density of cells in y direction vs cells in x direction. The leftmost is the initial density plot with a constant density of 1 throughout all 100 y cells between x-cells 0 through 50 and a constant density of 0.1 between x cells 0 through 100. The rightmost plot is the final density plot at t = 0.20 with a nonconstant density in x and constant density in y. A density of 1 transitions abruptly to a density 0.8 around x = 25 cells, then gradually lessens to 0.6 around x = 50 cells. An abrupt change occurs at x = 70 cells to a density of 0.3 and the final abrupt transition is at x = 90 cells to a density of 0.2
A skewer in x along the y and z midplanes yields the traditional 1-dimension solution, shown below (pink dots) plotted over the exact solution (purple line).
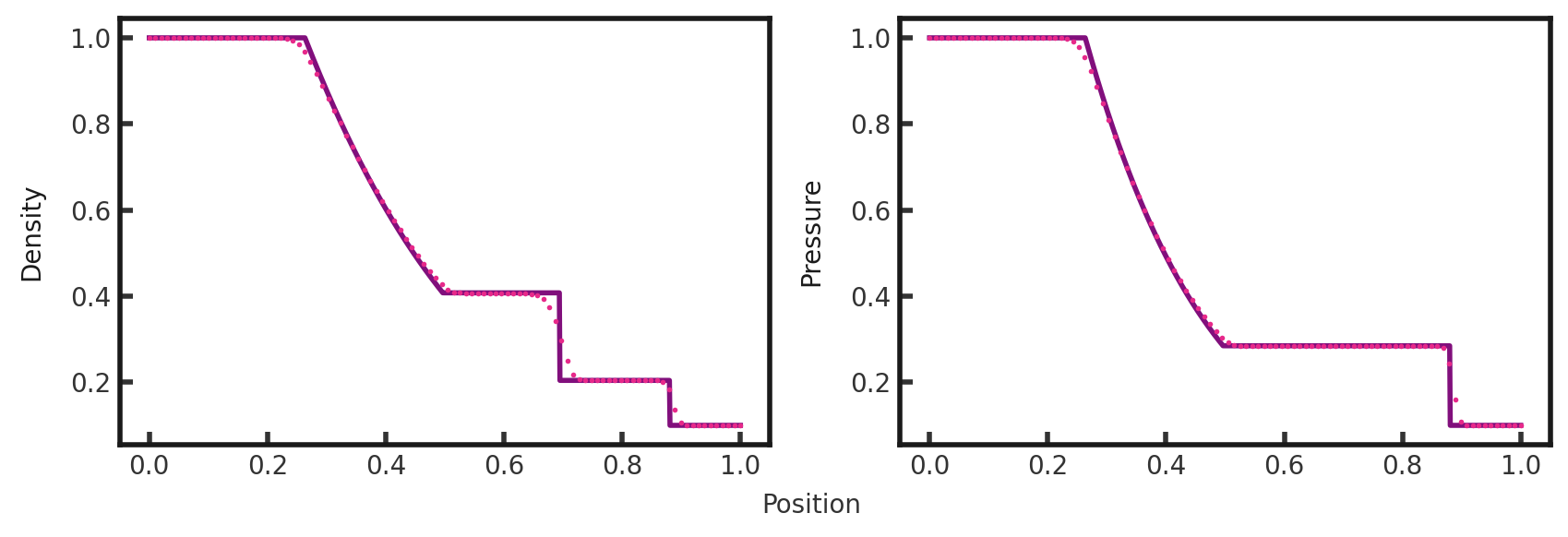
Two scatter plots side by side of density vs position and pressure vs position. The plots have pink dots plotted over a purple line. In all cases, the pink dots match the shape of the purple line, albeit imperfectly. The leftmost plot (density) shows a density of 1.0 for 0 \< x \< 0.2, then a continuous gradual decrease to a value of 0.4 at x = 0.5. Density remains constant until x = 0.7, then it jumps down abruptly to a value of 0.2. Density remains constant here until x = 0.9 where it makes a final jump to a value of 0.1, remaining at 0.1 for the final x values. The rightmost plot (final pressure) shows a pressure of 1.0 for 0 \< x \< 0.2, then a continuous gradual decrease to a value of 0.3 at x = 0.5. Pressure remains constant until x = 0.9 where it makes a jump to a value of 0.1, remaining at 0.1 for the final x values.
We can see a rarefaction wave on the left side, followed first by a contact discontinuity and then a shock.

Add a custom footer

Cholla Wiki

Physics

Testing

Examples

Advanced

In progress

Contributing

Clone this wiki locally