-
Notifications
You must be signed in to change notification settings - Fork 35
ECP Milestone 1.7: Kokkos contribution
SAND2017-11204 W
In this report we develop and port two QMCPACK kernels of the miniqmc miniapp (spline and Jastrow evaluations) to the Kokkos C++ programming model, and at least one CPU and one GPU based architecture. We make an initial assessment of:
- Capability (expressiveness, ability to achieve required levels of parallelization)
- Performance (achieved time to solution on multiple architectures)
- Portability (extent of modification required for performance on multiple architectures)
- Suitability (deviation from desired application abstractions required to port or to obtain performance, complexity, difficulty of learning curve)
- Support (compiler, tools, documentation)
Desired improvements and extensions to improve the objective (1-3) and subjective (4,5) measures will be identified and communicated with the Kokkos team.
In this initial assessment we concentrate on objective (1,3,4) with only a partial performance evaluation. Objective 5 is at this stage not a specific issue, since only production level compilers and tools are required for using Kokkos. A particular goal of this first porting approach to Kokkos is to leave the code structure of QMCPACK intact, and provide a minimally invasive implementation. As a consequence some possible optimization strategies, such as kernels which work on multiple walkers at the same time were not attempted. If this allows ultimately for satisfying performance, the approach would minimize the effort necessary to adopt Kokkos in QMCPACK. The work corresponds to the second stage porting effort outlined in the Sandia Technical Report SAND2015-7886 for an initial portable version.
Integrating Kokkos into the existing CMake build system is straight forward. Kokkos supports inclusion of its own CMake files into existing projects.
In the top level CMakeLists.txt we add:
######################################################
#KOKKOS Interaction
######################################################
set(CMAKE_CXX_EXTENSIONS OFF)
SET( KOKKOS_PATH "/home/crtrott/Kokkos/kokkos" )
add_subdirectory( ${KOKKOS_PATH} ${qmcpack_BINARY_DIR}/kokkos )
include_directories(${Kokkos_INCLUDE_DIRS_RET})
LINK_LIBRARIES(kokkos)
We also need to remove QMCPACKs internal settings for architecture flags, which
- didn't work on all platforms in the first place
- are now provided through Kokkos' CMake logic.
The net effect is a reduction of complexity of the build system. To provide architecture setting simply use the Kokkos options such as:
-DKOKKOS_HOST_ARCH=Power8
-DKOKKOS_GPU_ARCH=Pascal60
Currently for CUDA we require UVM as the memory space, which allows us to leave memory staging to the GPU memory to the driver runtime system. To configure on the Summit like testbeds use:
cmake -DKOKKOS_ENABLE_CUDA=true -DKOKKOS_ENABLE_OPENMP=false -DKOKKOS_ENABLE_CUDA_UVM=true -DCMAKE_CXX_COMPILER=${KOKKOS_PATH}/bin/nvcc_wrapper -DKOKKOS_GPU_ARCH=Pascal60 -DKOKKOS_HOST_ARCH=Power8 ../
On KNL use:
cmake -DKOKKOS_ENABLE_OPENMP=true -DCMAKE_CXX_COMPILER=icpc -DKOKKOS_HOST_ARCH=KNL ../
For the walker parallelization strategy a new capability in Kokkos called partitioning was utilized. It allows splitting of resources owned by the process over multiple master threads. For the Kokkos OpenMP backend this capability is implemented using OpenMP nested parallel execution. The outer level is utilized for walkers, while the inner levels are doing the parallelization for kernels acting on the data of each individual walker. Currently this approach is only available for the OpenMP backend, we expect it to be ready for CUDA in mid 2018. The fallback for CUDA compilation is to use a single walker per process, but launching multiple processes per GPU using the NVIDIA MPS server. The drawback of this approach is that otherwise shared data such as the spline arrays are duplicated in each process, similar to MPI only parallelization in the current QMCPACK production application.
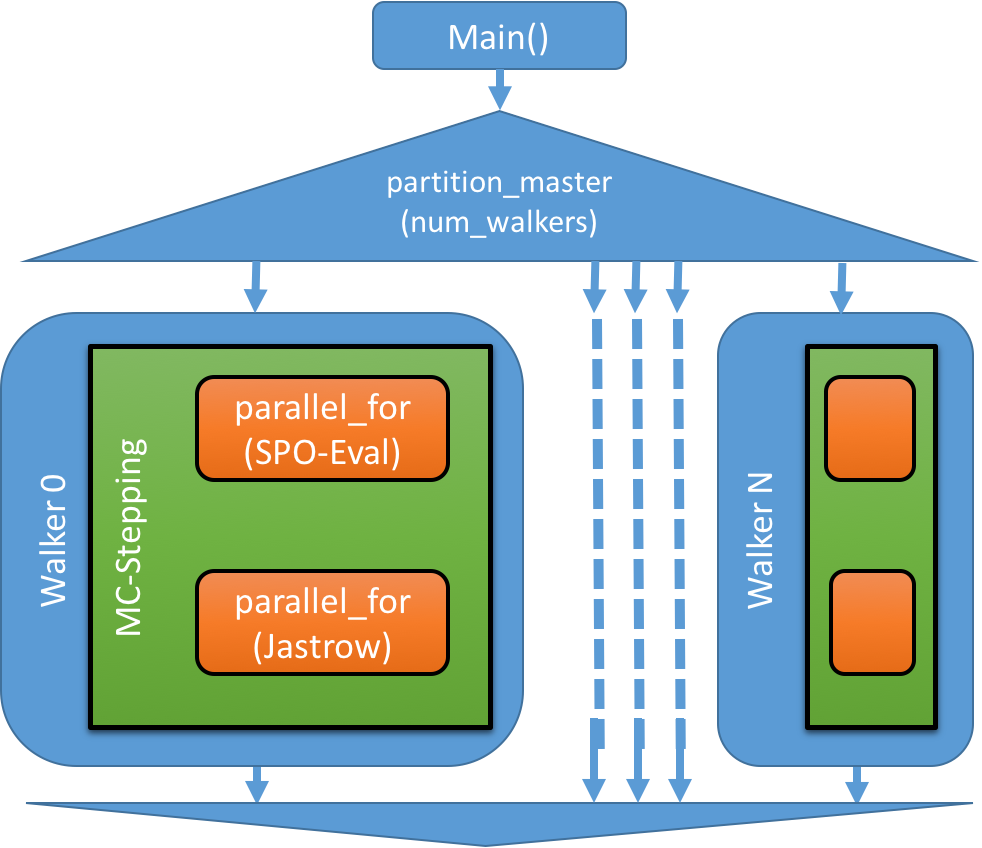
The code change to achieve the partitioning is to take the openMP parallel section in main() and change it into a C++11 lambda which is provided to the partition_master function of Kokkos:
// Old code
int main () {
...
#pragma omp parallel
{
// Walker Code Body
}
...
}
// New code
int main () {
...
auto main_function = [&] (int partition_id, int num_partitions) {
// Walker Code Body
}
Kokkos::partition_master(main_function,num_threads/ncrews,ncrews);
}Due to the above mentioned limitations in Kokkos the current partition_master call is implemented as:
#if defined(KOKKOS_ENABLE_OPENMP) && !defined(KOKKOS_ENABLE_CUDA)
int num_threads = Kokkos::OpenMP::thread_pool_size();
printf("Partitioning\n");
Kokkos::OpenMP::partition_master(main_function,num_threads/ncrews,ncrews);
#else
main_function(0,1);
#endif
Each Monte Carlo step requires the evaluation of single particle orbitals (SPOs). The miniqmc miniapp uses a 3D tricubic B-spline based orbital representation for the evaluation of the SPOs. The 3D tricubic B-spline basis is a highly efficient representation for SPOs requiring only 64 elements at any given point in space. The Kokkos implementation of the spline kernel requires modifications to the data structures and expression of parallelism in the mini-app.
The spline kernel evaluates the wavefunction, its gradient (a 3D vector containing the first derivative with respect to particle positions) and its hessian (a 3D tensor containing the second derivative with respect to particle positions). We convert several data structures related to these into Views which is the Kokkos abstraction for multidimensional arrays with template parameters controlling in which memory space (host or device) the data resides and which data layout is imposed. Generally all aligned_vector and std::vector objects which are accesses inside of parallel_for regions need to be replaced. The same is true for the VectorSoaContainer which is replaced with a 2D View. Note that the Layout of the 2D View is fixed to correspond with the legacy data layout for interoperability purposes during incremental Kokkos adoption.
For example in einspline_spo.hpp we replace:
using vContainer_type = aligned_vector<T>;
using gContainer_type = VectorSoaContainer<T, 3>;
using hContainer_type = VectorSoaContainer<T, 6>;with
using vContainer_type = Kokkos::View<T*>;
using gContainer_type = Kokkos::View<T*[3],Kokkos::LayoutLeft>;
using hContainer_type = Kokkos::View<T*[6],Kokkos::LayoutLeft>;Furthermore the spline class utilizes vectors of vectors for the psi grad and hess members, which are now replaced with Views of Views.
// Old
aligned_vector<vContainer_type *> psi;
aligned_vector<gContainer_type *> grad;
aligned_vector<hContainer_type *> hess;
// New
Kokkos::View<vContainer_type*> psi;
Kokkos::View<gContainer_type*> grad;
Kokkos::View<hContainer_type*> hess;This necessitates a particular way of allocation though using a placement new strategy:
// Old
psi.resize(nBlocks);
grad.resize(nBlocks);
hess.resize(nBlocks);
#pragma omp parallel for
for (int i = 0; i < nBlocks; ++i)
{
psi[i] = new vContainer_type(nSplinesPerBlock);
grad[i] = new gContainer_type(nSplinesPerBlock);
hess[i] = new hContainer_type(nSplinesPerBlock);
}
// New
psi = Kokkos::View<vContainer_type*>("Psi",nBlocks) ;
grad = Kokkos::View<gContainer_type*>("Grad",nBlocks) ;
hess = Kokkos::View<hContainer_type*>("Hess",nBlocks);
for(int i=0; i<psi.extent(0); i++) {
new (&psi(i)) vContainer_type("Psi_i",nSplinesPerBlock);
new (&grad(i)) gContainer_type("Grad_i",nSplinesPerBlock);
new (&hess(i)) hContainer_type("Hess_i",nSplinesPerBlock);
}
For the actual bspline struct we add an additional View member, but keep the old data handles available for interoperability purposes during an incremental Kokkos adoption. This again necessitates fixing the layout to the legacy layout, which in this case is not an issue since it is already optimal for the chosen parallelization strategy, which explicitly exploits vectorization on all architectures.
// Old
typedef struct
{
...
double *restrict coefs;
...
} multi_UBspline_3d_d;
// New
typedef struct
{
...
typedef Kokkos::View<double****, Kokkos::LayoutRight> coefs_view_t;
coefs_view_t coefs_view;
double *restrict coefs;
...
} multi_UBspline_3d_d;To allocate the splines we allocate the View first and then extract the raw data pointer:
spline->coefs_view = multi_UBspline_3d_d::coefs_view_t("Multi_UBspline_3d_d",Nx,Ny,Nz,N);
spline->coefs = spline->coefs_view.data();Deallocation generally relies on Kokkos' reference counting, and thus simply involves assigning a default constructure View:
// Old
class Allocator
{
template <typename SplineType> void destroy(SplineType *spline)
{
einspline_free(spline->coefs);
free(spline);
}
}
// New
class Allocator
{
template <typename SplineType> void destroy(SplineType *spline)
{
// Delete View by setting it to an empty view and rely on reference counting of views.
spline->coefs_view = typename SplineType::coefs_view_t();
free(spline);
}
}
A last data structure issue are static global variables utilized for the interpolation in MultiBsplineData. Such as global static variables are not supported on some architectures. We instead make them non-static members of the MultiBspline class, and initialize them before launching parallel kernels. At the same time we move the free compute_prefactor functions into the MultiBspline class as member functions.
By using the partitioning strategy for Walkers the parallel kernels actually look like top-level parallel dispatches in Kokkos, eliminating the need to think about that extra level while implementing the code for each Walker.
The basic approach is to parallelize over data blocks in the einspline_spo class. The original code looped over those blocks in its evaluate functions. For Kokkos parallelization we utilize its tagged operator capability, which enables a single class to act as the functor for multiple kernels. This is a strategy utilized in a number of class based applications for example in LAMMPS. What this entails is to copy the body of each parallel loop into its own operator member functions, which take a tag class as their first argument. These tag classes are defined as nested class definitions and are accompanied by corresponding execution policy typedefs:
struct einspline_spo {
...
struct EvaluateVTag {};
typedef Kokkos::TeamPolicy<EvaluateVTag> policy_v_t;
typedef typename policy_v_t::member_type team_v_t;
...
};The function split up into dispatch function and operator then becomes:
// Old
struct einspline_spo {
...
inline void evaluate_v(const pos_type &p)
{
auto u = Lattice.toUnit(p);
for (int i = 0; i < nBlocks; ++i)
compute_engine.evaluate_v(einsplines[i], u[0], u[1], u[2], psi[i]->data(), psi[i]->size());
}
};
// New
struct einspline_spo {
...
inline void evaluate_v(const pos_type &p)
{
pos = p;
is_copy = true;
compute_engine.copy_A44();
Kokkos::parallel_for("EinsplineSPO::evalute_v",policy_v_t(nBlocks,1,32),*this);
is_copy = false;
}
KOKKOS_INLINE_FUNCTION
void operator() (const EvaluateVTag&, const team_v_t& team ) const {
int block = team.league_rank();
// Need KokkosInlineFunction on Tensor and TinyVector ....
auto u = Lattice.toUnit(pos);
//
compute_engine.evaluate_v(team,&einsplines[block], u[0], u[1], u[2],
psi(block).data(), psi(block).extent(0));
}
};The attentive reader will notice some new things in the dispatch function. In particular arguments to the function need to be made members of the class, so that they are captured in the functor and accessible in the parallel code section. Furthermore, the functor (i.e. the einspline_spo class instance) will be captured by value and copy constructed. Since the class has View of Views data members which need to be manually deallocated, a is_copy flag needs to be added to prevent premature deallocation of data.
~einspline_spo()
{
if(! is_copy) {
if (psi.extent(0)) clean();
einsplines = Kokkos::View<spline_type *>() ;
}
}Another necessary change is the replacement of inline with KOKKOS_INLINE_FUNCTION for all functions which are subsequently called inside of the operator. For example:
template <typename T> struct MultiBspline
{
...
template<class TeamType>
KOKKOS_INLINE_FUNCTION
void evaluate_v(const TeamType& team, const spliner_type *restrict spline_m, T x, T y, T z, T *restrict vals, size_t num_splines) const;
...
}Furthermore, the team handle needs to be passed on for utilization of nested parallelism (including vector parallelism) in the evaluate function. In those functions loops decorated with #pragma omp simd are replaced with nested parallel_for calls using the Kokkos::ThreadVectorRange execution policy.
// Old
#pragma omp simd
for(int n=0; n<num_splines; n++) {
...
}
// New
Kokkos::parallel_for(Kokkos::ThreadVectorRange(team,num_splines),
[&](const int& n) {
...
});In this first pass through, we did not use Kokkos Views all the way down to the lowest level. The previous strategy of extracting the pointers from the aligned_vector class was kept in place.
Two evaluate function are called in the miniApp: evaluate_v and evaluate_vgh. The former requires a significantly lower amount of work, and is not profitable to internally parallelize for small problem sizes. Thus we add a runtime option based on a threshold, to whether execute it serially or in parlallel. This requires the addition of a number of typedefs, for defining different policy and member types.
struct EvaluateVTag {};
typedef Kokkos::TeamPolicy<Kokkos::Serial,EvaluateVTag> policy_v_serial_t;
typedef Kokkos::TeamPolicy<EvaluateVTag> policy_v_parallel_t;
typedef typename policy_v_serial_t::member_type team_v_serial_t;
typedef typename policy_v_parallel_t::member_type team_v_parallel_t;
inline void evaluate_v(const pos_type &p)
{
pos = p;
is_copy = true;
compute_engine.copy_A44();
if(nSplines > nSplinesSerialThreshold_V)
Kokkos::parallel_for("EinsplineSPO::evalute_v_parallel",policy_v_parallel_t(nBlocks,1,32),*this);
else
Kokkos::parallel_for("EinsplineSPO::evalute_v_serial",policy_v_serial_t(nBlocks,1,32),*this);
is_copy = false;
}While it would be possible to implement a templated operator, we simply opted to provide two copies, one taking a team_v_serial_t and one for team_v_parallel_t.
That said, evaluate_v is called in the second main loop of the main function to compute the NLPP energy, which with some further data structure changes would allow to exploit an additional level of parallelism. This strategy was not attempted yet, and remains to be done in future work.
The points discussed for the spline kernel apply equally for the Jastrow Kernels. Due to the limited amount of parallel work exposed in the original miniApp implementations, only a single team is launched though, and thus only vector parallelism is exploited. Furthermore, the utilization of the TinyVector and similar classes, requires the addition of KOKKOS_INLINE_FUNCTION in a significant amount of places for these helper objects. As discussed for the evaluate_v spline function above, it would be possible to exploit another level of parallelism in the main function, but this was not attempted for this time limited study.
Initial performance evaluations are performed on three Sandia testbed machines:
| Machine | CPU Type | Sockets x Cores x Threads | Memory |
|---|---|---|---|
| Shepard | Intel Haswell | 2 x 16 x 2 | 128GB DDR3 |
| Bowman | Intel KNL | 1 x 68 x 4 | 16GB HBM + 96GB DDR3 |
| White | IBM Power8 + NVIDIA P100 | 2 x 8 x 8 + 2 x 2 GPUs | 16GB HBM/GPU + 512GB DDR3 |
On Shepard performance tests were done with a single thread per core, using all 32 cores. On Bowman only 64 cores were utilized, with two threads per core. On White tests were run with a single GPU. White's GPUs are connected with NVLink to the IBM host CPUs.
At this point only the evaluation of the SPO in the diffusion section is reasonably well optimized (einspline_spo::evaluate_vgh). The other functions SPO evaluation and Jastrow functions are ported to Kokkos but no optimization attempts have been done, due to lack of time.
System sizes ranging from 384 electrons up to 12288 electrons were investigated, which should cover currently common problem sizes all the way to the ExaScale challenge problem. Not all sizes were run with the reference implementation, due to running out of memory, when restricted to a single thread per walker. With the Kokkos version it was possible to run the full range, with using multiple threads per Walker and thus less walkers per node.
Since the reference version does not provide thread parallelization inside individual walkers the comparison is run with a single thread per walker, as far as possible. On KNL this didn't work for larger problem sizes since the HBM memory is much more size constraint. For the larger problemsize of 6k electrons, 32 threads per walker were used on KNL.
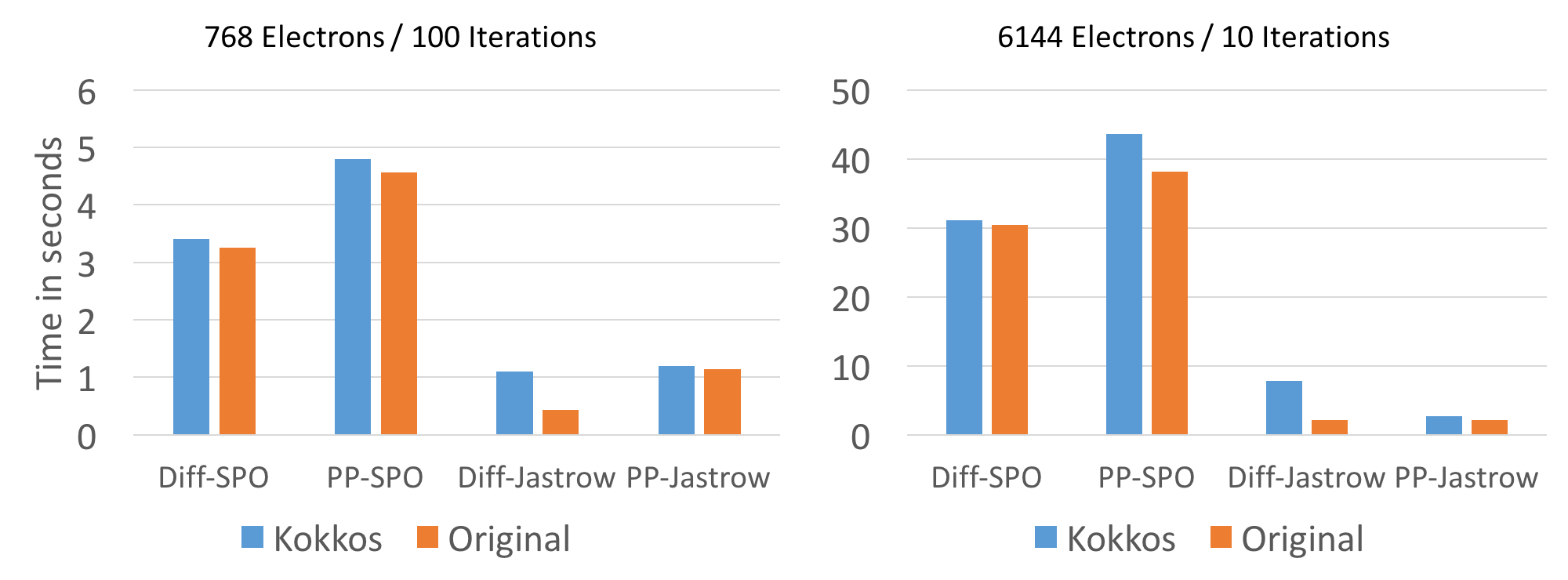
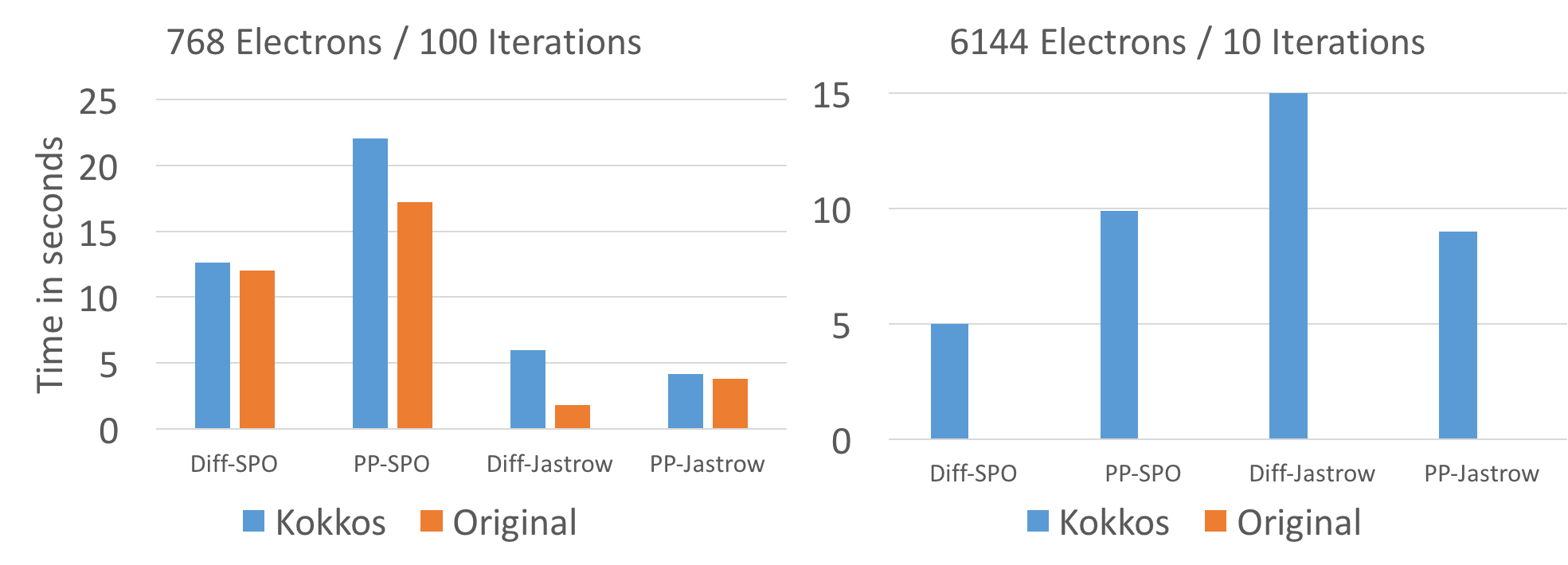
On CPU and KNL performance is very comparable to the reference version with the exception of the Diffusion Jastrow computation. The cause for that slowdown was not yet investigated. The reasonably well optimized diffusion SPO evaluation is with a few % points of the reference version.
Since the partition_master master capability is not yet available for the CUDA backend, the attempt was made to mimic the effect using multiple processes. The below plot shows the aggregate sampling rate for multiple concurrent processes sharing a single P100 GPU. The sampling rate is computed as num_walkers * num_iterations / time. Since only the SPO evaluation in Diffusion is reasonably optimized, the analysis is restricted to it.
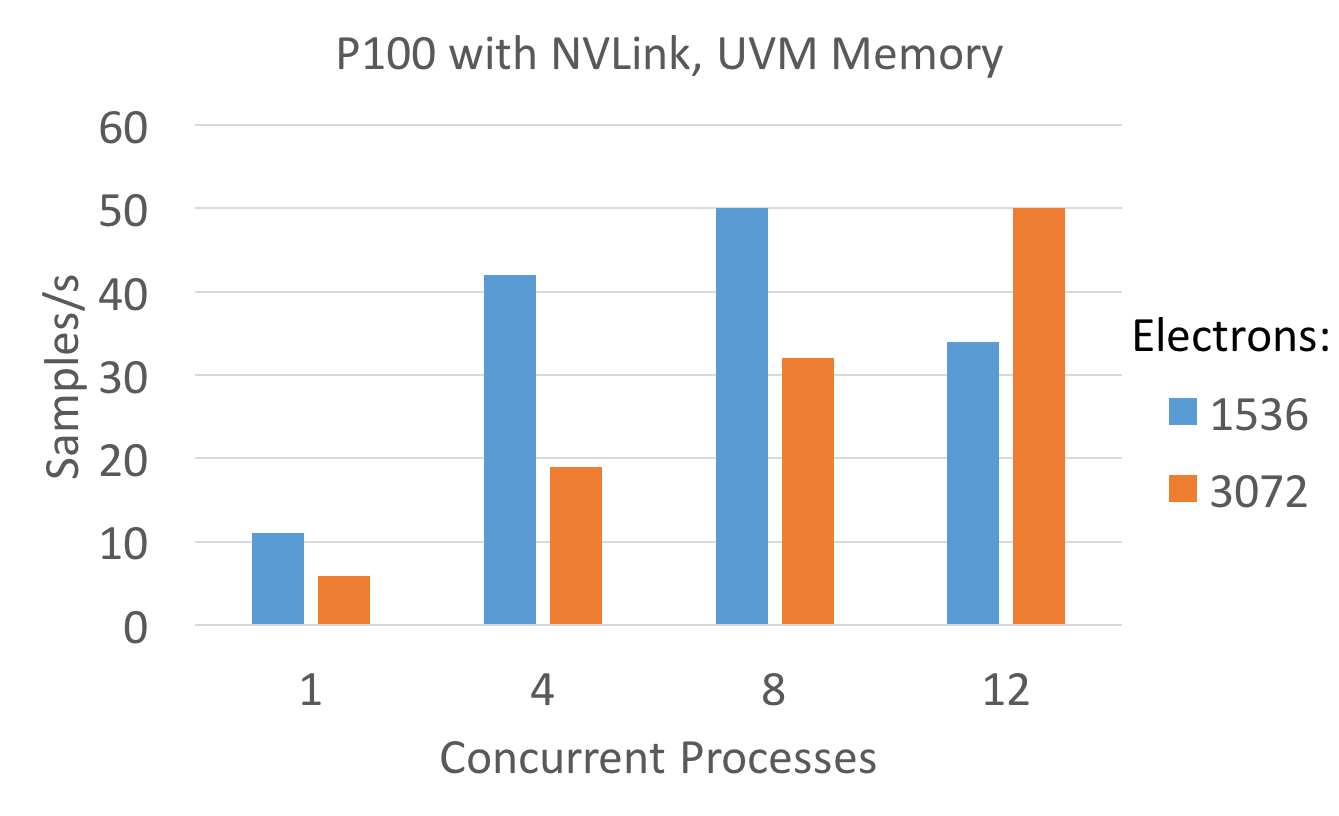
Ideally the aggregate sampling rate should be independent of the choice of how many walkers per node vs. how many threads per walker are used, as long as the total amount of threads is constant. This obviously breaks down for small problem sizes, where the amount of parallelism available within each walker is low. That said due to initilization cost it may be profitable to use multiple threads per walker, even if the sampling rate is somewhat lower, since more of the computed MC steps would be computational useful instead of consumed by system equilibration.
The following plot uses a Figure of Merit (FOM) for the SPO evaluation which is proportional to the achieved flop rate. It is computed as (num_walkers * num_iterations /time) * num_electrons * num_electrons * 1e-6.
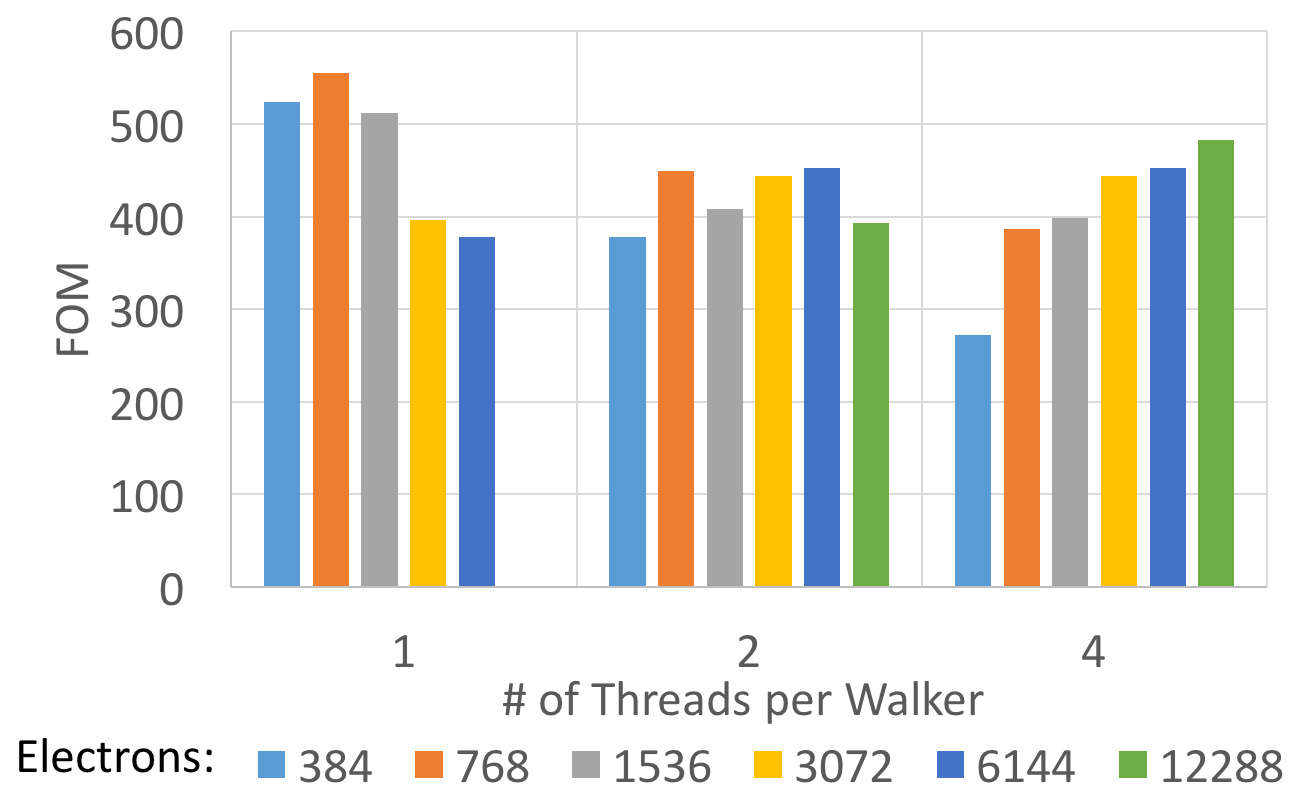
As can be seen for problem sizes larger than 2k electrons using multiple threads per walker always provides a benefit. Below that it may depend on the number equilibration vs. collection MC steps during a run.
Last but not least the following plot shows an architecture comparison, using the optimal choice of threads per walker for each problem size and architecture individually.

At 3k electrons largely equivalent performance is achieved across the three architectures, but while Haswell provides a flat performance profile, GPUs clearly need bigger problem sizes and KNL suffers at the largest problem sizes.
The GPU issues should be mitigated by a proper partition_master implementation in Kokkos, since it will eliminate a number of restrictions and performance issues caused by using multiple processes per GPU. The KNL performance degradation in particular at 12k electrons, might be caused by running the HBM memory close to its capacity limit, but a more detailed investigation will be necessary.
This research was supported by the Exascale Computing Project (ECP), Project Number: 17-SC-20-SC, a collaborative effort of two DOE organizations—the Office of Science and the National Nuclear Security Administration responsible for the planning and preparation of a capable exascale ecosystem including software, applications, hardware, advanced system engineering, and early testbed platforms to support the nation’s exascale computing imperative.