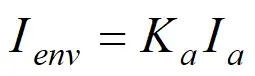本项目是一个基于TypeScript、浏览器Canvas,完全软光栅器实现。当然现实其实已经有很多非常出色的软光栅的项目,但难于这些项目依赖C++或一些图形库(GLFW)的支撑,学习成本较大,尤其我这样很少接触这些。如果基于浏览器Canvas渲染反馈,JavaScript实现光栅逻辑,基本上不需要配置复杂的环境。而且在调试上也有着巨大的优势,如利用浏览器的Devtools。
当然本项目适用于拥有一定的图形学基础、线代基础,因为在本文后部分,基于此项目会粗略讲解重要实现的部分,所以关于图形学、线代不会提及。但是,此项目也是我本人在入门完图形学(Games101)、以及拜读另一个软光栅项目tinyrender有感而发,用自己擅长的技术栈也去实现一个软光栅,在后面我也会分享一下我的学习路线,以及我的参考文章。
关于上面分别提到了TypeScript和JavaScript,原因是本项目是遵循工程化、模块化标准的一个Web前端项目,所以本质上最好打包后得到还是一个Html文件以及引用了一些JavaScript脚本文件,具体描述参考下方关于项目描述的介绍
基于TypeScript,ESM模块化标准,最后使用第三方库rollup等周边工具构建最终JavaScript单脚本文件,使用准备模板Html文件引入该脚本文件,当然静态文件Html已提前包含Cavans元素,因为此后渲染反馈载体都使用的是Cavans元素
此外为了提高开发便利性,如观察反馈效果、源码调试,使用nodemon +live-server做热重载刷新,且构建后JavaScript带持有源码TypeScript映射的SourceMap文件
本项目尽可能的不使用第三方库,唯一的模型解析除外,本项目模型文件使用的是.obj格式,所以采用了是webgl-obj-loader第三方库
- npm install 安装依赖
- npm run dev 启动项目
项目启动后,每当有文件变动的时都会触发TypeScipt编译、Rollup构建成单JavaScript脚本文件输出到dist目录,随后打开或刷新浏览器。dist目录下存放的项目生成的静态文件以及一些需要加载的纹理资源
{
"dependencies": {
"webgl-obj-loader": "^2.0.8"
},
"devDependencies": {
"@rollup/plugin-commonjs": "^26.0.1",
"@rollup/plugin-node-resolve": "^15.2.3",
"@rollup/plugin-typescript": "^11.1.6",
"concurrently": "^9.0.0",
"live-server": "^1.2.2",
"nodemon": "^3.1.4",
"rollup": "^4.21.0",
"typescript": "^5.5.4"
}
}├── dist //工程化打包后输出的目录,用浏览器打开.html静态文件,即可看到效果
├── src //工程化入库
│ ├── core //核心的模块,如camera、raster、shader等
│ ├── math //数学计算相关模块vector、matrix等
│ ├── model //模型源文件
│ ├── utils //工具函数、相关数据结构等
│ ├── app.ts //主入口
渲染的最终目标是视觉反馈,也就是图形显示的载体,在Html中 Canvas元素提供了一种渲染上下文CanvasRenderingContext2D,通过 canvas.getContext("2d")获取。随后将要渲染的帧数据通过context.putImageData(frameData)提交即可显示此次帧数据,frameData是一个ImageData对象,该对象可以理解成是一个w*h长度的数组,数组每连续四位元素记录坐标x,y像素上的的RGBA值。每个元素占用1字节8位,也就是我们常用的纹理格式RGBA8888。
通过new ImageData(width, height)即可得到一个widthXheight的帧数据,ImageData通过数组形式下标访问或修改元素值,如下例,生成的一个 100 * 100 ,颜色为红色的帧数据
具体使用以及详解可在MDN官网查询
const frameData = new ImageData(100, 100)
for (let offset = 0; offset < frameData.data.length; offset += 4) {
const [rIdx, gIdx, bIdx, aIdx] = [offset + 0, offset + 1, offset + 2, offset + 3]
frameData.data[rIdx] = 255
frameData.data[gIdx] = 0
frameData.data[bIdx] = 0
frameData.data[aIdx] = 255
}
const context = canvas.getContext("2d")
context.putImageData(frameData) 有了渲染载体,只需要在渲染主循环中变化帧数据,然后每次渲染将该数据提交给渲染上下文即可达到渲染效果。关于渲染主循环实现方式很多计时器、定时器都可以,但是本项目采用的是浏览器提供方法window.requestAnimationFrame,好处在于此方法执行频率可以匹配我们显示器刷新频率,且很方便我们统计当前帧数信息,参考下面代码,位于项目App.ts文件
// src/app.ts
class App {
private static raster: Raster
private static isMouseMoving: boolean = false
public static init(canvas: HTMLCanvasElement) {
const context = canvas.getContext("2d") as CanvasRenderingContext2D
this.raster = new Raster(canvas.width, canvas.height, context)
}
public static start() {
let last = 0
const loop = (timestamp: number) => {
const delt = timestamp - last
document.getElementById("fps")!.innerText = `FPS:${(1000 / delt).toFixed(0)}`
this.mainLoop()
last = timestamp
requestAnimationFrame(loop)
}
loop(0)
}
public static mainLoop() {
this.raster.render()
}
} 通过requestAnimationFrame每帧数执行我们的渲染主循环,执行完此次渲染逻辑后,随机注册下一帧的渲染逻辑,这样保证每帧渲染是连续性,且是有次序的,这也意味着若某一帧渲染耗时太久也会影响下一帧渲染时机,这也是我必须要保证的逻辑
此后,每帧循环执行的Raster的render方法,也是我们渲染的方法,看如下render 的实现:
// src/utils/frameBuffer.ts
export class FrameBuffer {
private data: ImageData
constructor(width: number, height: number) {
this.data = new ImageData(width, height)
}
public get frameData(): ImageData {
return this.data
}
}
// src/core/raster.ts
export class Raster {
private width: number
private height: number
private frameBuffer: FrameBuffer
private context: CanvasRenderingContext2D
constructor(w: number, h: number, context: CanvasRenderingContext2D) {
this.width = w
this.height = h
this.context = context
this.frameBuffer = new FrameBuffer(w, h)
}
public clear() {
for (let offset = 0; offset < this.frameBuffer.frameData.data.length; offset += 4) {
const [rIdx, gIdx, bIdx, aIdx] = [offset + 0, offset + 1, offset + 2, offset + 3]
this.frameBuffer.frameData.data[rIdx] = 0
this.frameBuffer.frameData.data[gIdx] = 0
this.frameBuffer.frameData.data[bIdx] = 0
this.frameBuffer.frameData.data[aIdx] = 255
}
}
public render() {
// 清理帧缓冲区
this.clear()
// 提交帧数据
this.context.putImageData(this.frameBuffer.frameData, 0, 0)
}
}注意对帧数据用类
FrameBuffer进行包装,方便后续提供一些其他操作方法
如上,Raster每帧在用黑色填充当前帧数据,然后将当前帧数据提交,因为目前在此中间比没有其他操作,所以目前我们看到Cavans一直处于黑色,且页面左上方会事实显示我们当前渲染的帧数
本项目模型使用的是.obj格式的模型文件,模型解析库使用的是
webgl-obj-loader,关于它的一个解析规则可在官方文档了解
目前没有任何东西在渲染,所以我们从导入模型开始,让屏幕能够渲染一些什么东西来。为了便捷我将模型源文件内容直接放入一个模块中,并将其内容作为字符串导出,方便可以对模型的解析,如下:
// src/model/african_head.ts
const fileText = `
v -0.3 0 0.3
v 0.4 0 0
v -0.2 0.3 -0.1
v 0 0.4 0
# 4 vertices
g head
s 1
f 1/1/1 2/1/1 4/1/1
f 1/1/1 2/1/1 3/1/1
f 2/1/1 4/1/1 3/1/1
f 1/1/1 4/1/1 3/1/1
# 4 faces
`
export default fileText 通过webgl-obj-loader库对模型进行解析,如下代码,对redner函数增加了渲染模型顶点的逻辑,以模型三角形顶点数量为循环,以此将模型顶点在帧数据中的像素位置的赋予红色。
注意这里的使用的模型在项目中已提供,位于`/src/model/african_head.ts
// src/utils/frameBuffer.ts
export class FrameBuffer {
// ......
public setPixel(x: number, y: number, rgba: [number, number, number, number]): void {
x = Math.floor(x)
y = Math.floor(y)
if (x >= this.data.width || y >= this.data.height || x < 0 || y < 0) return
this.data.data[((y * this.data.width + x) * 4) + 0] = rgba[0]
this.data.data[((y * this.data.width + x) * 4) + 1] = rgba[1]
this.data.data[((y * this.data.width + x) * 4) + 2] = rgba[2]
this.data.data[((y * this.data.width + x) * 4) + 3] = rgba[3]
}
// ......
}
// src/core/raster.ts
import { Mesh } from "webgl-obj-loader";
import african_head from "../model/african_head";
export class Raster {
constructor(w: number, h: number, context: CanvasRenderingContext2D) {
// .......
this.model = new Mesh(african_head)
this.vertexsBuffer = this.model.vertices
this.trianglseBuffer = this.model.indices
// .......
}
public render() {
// 清理帧缓冲区
this.clear()
// 遍历模型的三角面
for (let i = 0; i < this.trianglseBuffer.length; i += 3) {
for (let j = 0; j < 3; j++) {
const idx = this.trianglseBuffer[i + j]
const vertex = new Vec3(this.vertexsBuffer[idx * 3 + 0], this.vertexsBuffer[idx * 3 + 1], this.vertexsBuffer[idx * 3 + 2])
this.frameBuffer.setPixel(vertex.x,vertex.y,[255,0,0,255])
}
}
// 提交帧数据
this.context.putImageData(this.frameBuffer.frameData, 0, 0)
}
} 当然这样逻辑去渲染的话,最终得出效果肯定是不符合预期的,原因也很明显坐标系的差异,模型、屏幕都有着自己的坐标系,也就是所谓的模型空间、屏幕空间,当然还有一个的世界空间,观察空间,所以下面开始第四部分矩阵变化变化,就包含上述的不同坐标系间的转换。注意,这里模型坐标系以及平屏幕坐标系初始是被固定的
- 屏幕坐标系:依赖的是
Cavans,原点在左上角,范围在0-width,0-height,没有负值 - 模型坐标系:项目中的模型的原点为(0,0,0),x,y,z范围在-1,1,也就是被包含在一个长度为2的立方体中,原点在这个立方体的中心
这里的矩阵变化属于是图形学中部分,所以具体理论和推导就不多复述了,以及投影矩阵部分,为了不增加复杂度,后面讲解基于正交投影,当然项目也有透视投影矩阵,可以切换相机类型达到透视投影效果
模型矩阵作用将模型空间转换到世界空间,这里我们定义模型的位置就是放在世界坐标系的原点,因为模型的坐标x,y,z在-1,1的立方体中,为了变得显而易见,我们要对模型进行缩放,并且考虑为了方便后续相机的观察,这里将模型Z坐标移动-240,负值是因为本项目基于右手坐标系,相机默认向-z方向看,所以最终得到下面的矩阵
this.modelMatrix = new Matrix44([
[240, 0, 0, 0],
[0, 240, 0, 0],
[0, 0, 240, -240],
[0, 0, 0, 1]
]) 视图矩阵的目的将世界坐标系转换到相机的观察坐标系,也可以理解统一这俩坐标系,方面后续的计算。因为本项目是基于右手坐标系,所以X 轴叉乘 Y 轴等于+Z轴,Y 轴叉乘 Z 轴等于+X轴。下面是个人对于视图变化的一个理解
原相机:原本和世界坐标系重合的相机
现在相机:原相机经过矩阵变化后等到现在的相机状态,也就是pos,lookAt,up组成的状态
- 视图变化目的就是将世界坐标系和相机坐标做一个统一,方便后面投影计算,因为统一了坐标系,默认将原点作为投影的出发点定义一些平面和参数
- 首先一个常识问题,对一个物体和相机以相同的方向和角度旋转,相机所观察到的画面是不不会变的,以互为相反的方向旋转,相机所观察的画面是我们显示生活中看到的画面
- 想象原相机在世界坐标系下原点位置,在经过旋转、平移等操作后,得到我们现在的相机状态,也就是相机坐标系,vecZ,vecX,vecY
- 由矩阵的本质,相机旋转、平移操作矩阵本质上就是现在相机坐标系的基向量,可以理解为原本和世界坐标系重合的相机经过现在的相机的基向量坐标系进行的矩阵变化
- 理论上我们只要将世界坐标系下的所有点都转换到相机坐标系下,也就是将所有世界左边乘上如今相机的基向量的组成的矩阵,由于相机操作和物体操作时相反的,所以应该是乘上如今相机的基向量的组成的矩阵的逆矩阵
为了方便后续动态的旋转平移,本项目将视图矩阵由初始的视图矩阵和动态变化矩阵组合而成的,如下:
// src/core/camera.ts
export class Camera {
//......
public look(): Matrix44 {
// 通过pos、lookAt、up求求现在相机的基向量
const vecZ = this.pos.sub(this.lookAt).normalize()
const vecX = this.up.cross(vecZ).normalize()
const vecY = vecZ.cross(vecX).normalize()
const revTransMat = new Matrix44([
[1, 0, 0, -this.pos.x],
[0, 1, 0, -this.pos.y],
[0, 0, 1, -this.pos.z],
[0, 0, 0, 1]
])
const revRotationMat = new Matrix44([
[vecX.x, vecX.y, vecX.z, 0],
[vecY.x, vecY.y, vecY.z, 0],
[vecZ.x, vecZ.y, vecZ.z, 0],
[0, 0, 0, 1]
])
// 合成view矩阵,先平移后旋转
return revRotationMat.multiply(revTransMat)
}
public getViewMat(): Matrix44 {
const baseViewMat = this.look()
return this.transMatExc.transpose().multiply(this.rotationMatExc.transpose().multiply(baseViewMat))
}
}这里讲解投影矩阵基于正交投影
投影矩阵顾名思义就是将被可视的空间投影到2D平面上,3D到2D的一个变化,所以一般来说我会定义一个被可视的空间,也就是会用一个远平面和近平面组成的长方体或锥体来定义这样的被可视空间。值得注意的是,近远平面的位置坐标应该基于相机坐标系,因为当要进行到投影矩阵变化时,此时已经经过模型变化、视图变化,所以此时所有坐标点已经在相机坐标系下,相机坐标系原点便是相机所在的位置。所以本项目近远平面的z坐标都是负值,因为相机在原点,向-Z轴看。
按照正交投影的性质,我们这里可视的空间是一个长方体,近远平面都在负Z半轴上,并定义近远平面宽高和屏幕宽高保持一致,也就是Canvas的宽高,随后将该可视空间长方体中心点平移到原点上,再将该长方体压缩成一个长度为2的一个标准立方体,既XYZ坐标的范围在-1到1。这样做目的好处如下
- 可视空间外被剔除不渲染,即观察空间(相机下的坐标系)下坐标不在这个标准正方体内的点
- 方便后续的视口矩阵变化计算,即将可是空间点真正的映射到屏幕像素
// src/core/camera.ts
export class Camera {
//......
public orthogonal(): Matrix44 {
const left = -this.screenWidth / 2
const right = this.screenWidth / 2
const bottom = -this.screenHeight / 2
const top = this.screenHeight / 2
const scaleMat = new Matrix44([
[2 / (right - left), 0, 0, 0],
[0, 2 / (top - bottom), 0, 0],
[0, 0, 2 / (this.near - this.far), 0],
[0, 0, 0, 1]
])
const transMat = new Matrix44([
[1, 0, 0, -((right + left) / 2)],
[0, 1, 0, -((top + bottom) / 2)],
[0, 0, 1, -((this.far + this.near) / 2)],
[0, 0, 0, 1]
])
return scaleMat.multiply(transMat)
}
} 视口变化也是最后的一个矩阵变化,再经过上一步的投影变化后,可视空间已经被压缩在一个标准被立方体中,如果按照正交投影方式,会直接丢弃z坐标,那么可是空间就被映射在一个x,y范围在-1至1的的平面中。
最重要的是我们屏幕分辨率不是固定的,且坐标系也是不同的,所以最后视口矩阵变化就是将这个2d平面转换到屏幕坐标系下,在本项目中也就是canvas。
值得注意的是,y坐标缩放是个负值,原因是canvas的原点在左上角,且y轴向下,所以这里需要对y坐标进行反转。
this.viewPortMatrix = new Matrix44([
[this.width / 2, 0, 0, this.width / 2],
[0, -this.height / 2, 0, this.height / 2],
[0, 0, 1, 0],
[0, 0, 0, 1]
]) 最终得到这四个变化矩阵后,对空间中所有点都进行这个四个矩阵变化,最后输出的坐标便是屏幕上的像素坐标,对所有点应用矩阵变化便就是vertexShader(顶点着色器),也就是下面提到的着色器部分。
经过上文,已经得到将空间中任意的点转换到屏幕中的像素点的变化矩阵,值得注意的是,并不是所有的点都能有对应的屏幕像素点,因为有相机的存在,不可见的是会被裁剪的。
顶点着色器,输入空间中的点坐标输出屏幕中像素点坐标,转换的逻辑便是引用上述的四个矩阵变化。输入的点便上我们模型的所有顶点,如下:
// scr/core/shader.ts
export class FlatShader extends Shader {
public vertexShader(vertex: Vec3): Vec4 {
const modelMatrix = this.raster.modelMatrix
const viewMatrix = this.raster.viewMatrix
const projectionMatrix = this.raster.projectionMatrix
const mvpMatrix = projectionMatrix.multiply(viewMatrix.multiply(modelMatrix))
const viewPortMatrix = this.raster.viewPortMatrix
const mergedMatrix = viewPortMatrix.multiply(mvpMatrix)
return mergedMatrix.multiplyVec(new Vec4(vertex.x, vertex.y, vertex.z, 1))
}
}
// src/core/raster.ts
export class Raster {
public render() {
// 遍历模型的三角面
for (let i = 0; i < this.trianglseBuffer.length; i += 3) {
for (let j = 0; j < 3; j++) {
const idx = this.trianglseBuffer[i + j]
const vertex = new Vec3(this.vertexsBuffer[idx * 3 + 0], this.vertexsBuffer[idx * 3 + 1], this.vertexsBuffer[idx * 3 + 2])
const vertexScreen = this.shader.vertexShader(vertex)
this.frameBuffer.setPixel(vertexScreen.x,vertexScreen.y,[0,255,0,255])
}
}
}
} 最终看到的效果便如上图,为了验证矩阵的正确性,这边监听鼠标拖动来动态调整相机的角度,如下代码:
// src/app.ts
class App {
public static onMouseUp(e: MouseEvent) { this.isMouseMoving = false }
public static onMouseDown(e: MouseEvent) { this.isMouseMoving = true }
public static onMouseMove(e: MouseEvent) {
if (!this.isMouseMoving) return
this.raster.camera.rotatedCamera(new Matrix44().rotateY(Math.sign(e.movementX) * 2 / 180 * Math.PI))
}
}
canvas.onmousedown = App.onMouseDown.bind(App)
canvas.onmouseup = App.onMouseUp.bind(App)
canvas.onmousemove = App.onMouseMove.bind(App)
// src/core/camera.ts
export class Camera {
public rotatedCamera(mat: Matrix44): void {
this.rotationMatExc = mat.multiply(this.rotationMatExc)
}
} 上述代码通过监听鼠标的按住拖动,生成一个绕Y轴旋转的旋转矩阵,并让更新相机一个rotationMatExc矩阵,此处rotationMatExc矩阵在上文3.4.2中提及过,以及它的设计目的。我们来长按拖动鼠标看到如下效果:
上述效果有个明显问题,我们旋转的是相机,当我们相机朝一个角度旋转时,当旋转到180度时,此时模型应该已经在我们相机背面,应该什么都看不到。
这个问题产生的原因:没有进行空间裁剪,可视空间在正交投影时已经压缩到一个标准立方体中,各坐标范围在-1致1,随后在通过一个视口变化,转换成屏幕的坐标。首先这里正交投影抛弃z(深度信息)坐标,就是z坐标不在-1至1仍然参与后续的视口变化转换成屏幕坐标,这便是问题所在,z坐标不在-1,1之内的点,说明这些点并不在可视空间内,并不需要渲染。处理方式的很简单,首先在视口变化中并没有对z坐标处理,所以转换成屏幕坐标后,z坐标仍是之前经过正交矩阵变化的后的z坐标,所以通过以下代码:
// src/core/raster.ts
export class Raster {
public render() {
// 遍历模型的三角面
for (let i = 0; i < this.trianglseBuffer.length; i += 3) {
for (let j = 0; j < 3; j++) {
//......
if (vertexScreen.z < -1 || vertexScreen.z > 1) continue
const vertexScreen = this.shader.vertexShader(vertex)
this.frameBuffer.setPixel(vertexScreen.x,vertexScreen.y,[0,255,0,255])
}
}
}
} 当然x y坐标不在-1,1范围内理论上也是不需要渲染,也需要裁剪掉,此项目这里不处理的原因是,在做视口变化后,x,y都转换成屏幕坐标,当设置像素时,超过屏幕高度和宽度的像素都是不生成的,frameBuffer的setPixel方法
public setPixel(x: number, y: number, rgba: [number, number, number, number]): void {
x = Math.floor(x)
y = Math.floor(y)
if (x >= this.data.width || y >= this.data.height || x < 0 || y < 0) return
this.data.data[((y * this.data.width + x) * 4) + 0] = rgba[0]
this.data.data[((y * this.data.width + x) * 4) + 1] = rgba[1]
this.data.data[((y * this.data.width + x) * 4) + 2] = rgba[2]
this.data.data[((y * this.data.width + x) * 4) + 3] = rgba[3]
}关于判断点是否再三角形内,有很多种方式,如向量叉乘等,本项目采用的是重心判断,感兴趣可以自行学习了解。使用重心原因为后续会用到一些插值。
目前我们只是简单通过渲染顶点来观察这个模型,接下来开始着手渲染面,也就是三角形,也是光栅化比较重要部分,通过填充再三角面内的像素,达到渲染面效果,所以也就是判断像素是否再某个三角形面,有俩种实现方式
- 遍历屏幕所有像素,挨个判断该像素是否再这个三角形中,性能差
- 通过一个最小包围盒包裹住该三角形,对包围盒的像素遍历,判断是否再三角形中,性能优
这里需要来改造一下render函数,并新增一个triangle,如下:
public render() {
// 清理帧缓冲区
this.clear()
// 重置变化矩阵
this.resetMatrix()
for (let i = 0; i < this.trianglseBuffer.length; i += 3) {
const oriCoords = []
const screenCoords = []
// 顶点计算: 对每个顶点进行矩阵运算(MVP),输出顶点的屏幕坐标,顶点着色阶段
for (let j = 0; j < 3; j++) {
const idx = this.trianglseBuffer[i + j]
const vertex = new Vec3(this.vertexsBuffer[idx * 3 + 0], this.vertexsBuffer[idx * 3 + 1], this.vertexsBuffer[idx * 3 + 2])
screenCoords.push(this.shader.vertexShader(vertex, idx * 3))
}
// 绘制三角形:通过三个顶点计算包含在三角形内的屏幕像素,并对包含像素上色,片元着色阶段
this.triangle(screenCoords)
}
}
public triangle(screenCoords: Array<Vec3>) {
const minx = Math.floor(Math.min(screenCoords[0].x, Math.min(screenCoords[1].x, screenCoords[2].x)))
const maxx = Math.ceil(Math.max(screenCoords[0].x, Math.max(screenCoords[1].x, screenCoords[2].x)))
const miny = Math.floor(Math.min(screenCoords[0].y, Math.min(screenCoords[1].y, screenCoords[2].y)))
const maxy = Math.ceil(Math.max(screenCoords[0].y, Math.max(screenCoords[1].y, screenCoords[2].y)))
for (let w = minx; w <= maxx; w++) {
for (let h = miny; h <= maxy; h++) {
const bar = barycentric(screenCoords, new Vec3(w, h, 0))
// 不在三角面内的像素点不进行着色
if (bar.x < 0 || bar.y < 0 || bar.z < 0) continue
// 计算插值后该像素的深度值,并进行深度测试
const depth = this.depthBuffer.get(w, h)
const interpolatedZ = bar.x * screenCoords[0].z + bar.y * screenCoords[1].z + bar.z * screenCoords[2].z
if (interpolatedZ < -1 || interpolatedZ > 1 || interpolatedZ < depth) continue
// 调用片元着色器,计算该像素的颜色
const color = this.shader.fragmentShader(bar)
this.depthBuffer.set(w, h, interpolatedZ)
this.frameBuffer.setPixel(w, h, color)
}
}
} 如上述代码,依次对每个三角形三个顶点调用vertexShader得到屏幕到像素点坐标,随后交给triangle处理,这里采用的是包围盒算法,去一个最小的包围盒包裹该三角形,遍历这些可能存在于三角形内的像素点,以此做是否再三角形内、深度测试,最后将通过测试的像素交给fragmentShader获取该像素最终的颜色。
值得注意的是深度测试放到此处,原因此时开始渲染面,丢弃应该是像素点,而不是之前粗暴的顶点。到这里我们开始处理fragmentShader的逻辑了。
片元着色器输入当前像素信息,输出该像素的颜色值。但常常输入是该像素的在三角形内的重心坐标,方便后续应用着色模型运用插值。为了快速看到我们加入面处理后的效果,这里我们FragmentShader只是简单通过输入的像素,输出一个固定的白色,如下效果:
// src/core/shader.ts
public fragmentShader(barycentric: Vec3): [number, number, number, number] {
return [255, 255, 255, 255]
} 很明显上述效果并不是我们想要,也是在意料之中。首先我们对每个所有三角面内的所有颜色都采用一种颜色,所以导致的这样结果。首先,模型本身所有三角面角度是不一致(法向量各不相同),也就是模型表面应该是凹凸不平的,现实生活中某个方向有一道平行光,模型每个地方接受的光是不相等,所以模型表面反射光的强弱是不一致的,也导致作为观察者,看去模型各个地方颜色也是不一致的。
以上便是着色模型的思想,物体表面的颜色受关照和材质影响,所以本文考虑最简单光照,平行光,首先我们定一个平行光,如对着模型正方向的平行光,也就是往-z轴照去的光:
// src/core/raster.ts
this.lightDir = new Vec3(0, 0, -1)有了平行光,此刻只要计算出光照强度,也就是平行光和面(像素、点)的法向量夹角。至于是以像素为计算夹角还是整个计算夹角,这便是着色频率的思想,如我计算一个三角面的光照强度,在这平面内所有像素都采用该光照强盗影响下的颜色,以此类推,以像素,以顶点,这也是常规的三种着色频率flat、gouraud、phone,这三种分别对应着逐面 、逐顶点、逐像素,为了方便观察效果的变化,我们采用最简单的flat着色频率,如下代码实现和效果:
// src/core/shader.ts
export class FlatShader extends Shader {
private normal: Vec3 = new Vec3(0, 0, 0)
private lightIntensity: number = 0
public vertexShader(vertex: Vec3): Vec3 {
if (this.vertex.length == 3) this.vertex = []
this.vertex.push(vertex)
if (this.vertex.length == 3) {
this.normal = this.vertex[1].sub(this.vertex[0]).cross(this.vertex[2].sub(this.vertex[0])).normalize()
this.lightIntensity = Vec3.dot(Vec3.neg(this.raster.lightDir).normalize(), this.normal)
}
// mvp、viewport
const modelMatrix = this.raster.modelMatrix
const viewMatrix = this.raster.viewMatrix
const projectionMatrix = this.raster.projectionMatrix
const mvpMatrix = projectionMatrix.multiply(viewMatrix.multiply(modelMatrix))
const viewPortMatrix = this.raster.viewPortMatrix
const mergedMatrix = viewPortMatrix.multiply(mvpMatrix)
return mergedMatrix.multiplyVec(new Vec4(vertex.x, vertex.y, vertex.z, 1)).toVec3()
}
public fragmentShader(barycentric: Vec3): [number, number, number, number] {
return [255 * this.lightIntensity, 255 * this.lightIntensity, 255 * this.lightIntensity, 255]
}
} 在顶点着色阶段便计算当前三角面的法向量,随后便计算出该面的光照强度并记录,在偏远着色阶段时,直接对面内所有像素采用同光照强度下的颜色值。
值得注意的是,这里将光照方向取反了,原因我们定义的光照是一个向量,表示一个方向,所以在计算夹角时,应取反。
观察上面效果可能会有疑问,为什么旋转时脸部一直都是最亮的状态,原因是我们旋转的是相机,光照方向和模型的位置都没有发生变化,所以脸部一直都是最亮的状态。
该着色频率便是逐顶点的,通过三角面三个顶点的法向量计算出对应的光照强度,随后对内部所有像素插值得出该像素的光照强度,直接上代码:
export class GouraudShader extends Shader {
private lightIntensityVetex: Array<number> = []
public vertexShader(vertex: Vec3, idx: number): Vec3 {
if (this.vertex.length == 3) {
this.vertex = []
this.lightIntensityVetex = []
}
this.vertex.push(vertex)
const vertexNormals = this.raster.model.vertexNormals
const vertexNormal = new Vec3(vertexNormals[idx], vertexNormals[idx + 1], vertexNormals[idx + 2]).normalize()
this.lightIntensityVetex.push(Vec3.dot(vertexNormal, Vec3.neg(this.raster.lightDir).normalize()))
// mvp、viewport
const modelMatrix = this.raster.modelMatrix
const viewMatrix = this.raster.viewMatrix
const projectionMatrix = this.raster.projectionMatrix
const mvpMatrix = projectionMatrix.multiply(viewMatrix.multiply(modelMatrix))
const viewPortMatrix = this.raster.viewPortMatrix
const mergedMatrix = viewPortMatrix.multiply(mvpMatrix)
return mergedMatrix.multiplyVec(new Vec4(vertex.x, vertex.y, vertex.z, 1)).toVec3()
}
public fragmentShader(barycentric: Vec3): [number, number, number, number] {
const lightIntensity = this.lightIntensityVetex[0] * barycentric.x + this.lightIntensityVetex[1] * barycentric.y + this.lightIntensityVetex[2] * barycentric.z
return [255 * lightIntensity, 255 * lightIntensity, 255 * lightIntensity, 255]
}
} 值得注意的是,这里再片元着色阶段,使用到传入的重心坐标,这个重心坐标也是上面提到再做深度测试以及判断是否在三角形内使用到。
该着色频率便是逐像素,根据每个像素自身的法向量来计算光照强度,随后对该像素应用对于光照强度的下的颜色值。关于每个像素的法向量并不是能直接得到的,这里需要一张法线贴图或切线贴图,这贴图也是一种纹理,纹理颜色值记录的表示的是法向量,所以在一个三角面内,通过三个顶点的uv坐标插值计算出对应像素的uv坐标,在从法线贴图中获取该像素的法向量,从而得到光照强度,计算该像素的最终颜色。
这个涉及到了关于纹理的采样,这块的实现在下一小节就会提及,所以这里我们先不关心纹理采样的逻辑,只去实现这样的着色频率逻辑,上代码:
export class PhoneShader extends Shader {
private textureVetex: Array<Vec3> = []
public vertexShader(vertex: Vec3, idx: number): Vec3 {
if (this.vertex.length == 3) {
this.vertex = []
this.textureVetex = []
}
this.vertex.push(vertex)
const vertexTextures = this.raster.model.textures
this.textureVetex.push(new Vec3(vertexTextures[idx], vertexTextures[idx + 1], 0))
// mvp、viewport
const modelMatrix = this.raster.modelMatrix
const viewMatrix = this.raster.viewMatrix
const projectionMatrix = this.raster.projectionMatrix
const mvpMatrix = projectionMatrix.multiply(viewMatrix.multiply(modelMatrix))
const viewPortMatrix = this.raster.viewPortMatrix
const mergedMatrix = viewPortMatrix.multiply(mvpMatrix)
return mergedMatrix.multiplyVec(new Vec4(vertex.x, vertex.y, vertex.z, 1)).toVec3()
}
public fragmentShader(barycentric: Vec3): [number, number, number, number] {
const u = this.textureVetex[0].x * barycentric.x + this.textureVetex[1].x * barycentric.y + this.textureVetex[2].x * barycentric.z
const v = this.textureVetex[0].y * barycentric.x + this.textureVetex[1].y * barycentric.y + this.textureVetex[2].y * barycentric.z
const normalColor = this.raster.textureNormal.sampling(u, v)
let lightIntensity = 1
if (normalColor) {
const normal = new Vec3(normalColor[0] * 2 / 255 - 1, normalColor[1] * 2 / 255 - 1, normalColor[2] * 2 / 255 - 1).normalize()
lightIntensity = Vec3.dot(Vec3.neg(this.raster.lightDir).normalize(), normal)
}
if (normalColor) return [255 * lightIntensity, 255 * lightIntensity, 255 * lightIntensity, 255]
return [255, 255, 255, 255]
}
} 如上述代码在顶点着色阶段,记录每个顶点的uv坐标,随后在偏远阶段插值计算当前像素的uv坐标,随后通过this.raster.textureNormal.sampling(u, v)从法线贴图中获取一个记录法向量的颜色值,中间需要对颜色值转换成法向量,这是一个固定计算方式,取决于法线贴图的生成。
这里对normalColor进行判断原因在于因为纹理作为图片是异步加载的,可能存在贴图还未加载完成。看下实际效果,明显相比前俩中着色频率,细节更加丰富:
本项目为了方便加载,所有贴图都放在项目./dist目录下
在上一节中介绍了三种着色频率,基于一种平行光,根据不同光照强度采用不同亮度的颜色。所以对于平行光的背面,以为光照强度为0,意味着没有任何颜色,这完全是不符合现实的。模型有着自身的颜色,也就是贴图,光照只会影响面的亮度。贴图通过uv坐标记录着模型中所有用到的颜色值。
因本项目基于web浏览器,所以加载都是通过Http请求加载图片,所以生成纹理是异步的过程。对加载好的图片,使用canvas对其解码展开,得到对应的纹理格式数据(位图)。具体看如下代码:
// scr/core/texture.ts
export class Texture {
private image: HTMLImageElement
private loaded: boolean = false
private textureData: ImageData
constructor(src: string) {
this.image = new Image()
this.image.src = src
this.image.onload = () => {
const canvas = document.createElement('canvas')
canvas.width = this.image.width
canvas.height = this.image.height
const context = canvas.getContext('2d')
context.drawImage(this.image, 0, 0)
this.textureData = context.getImageData(0, 0, canvas.width, canvas.height)
this.loaded = true
}
}
public sampling(u: number, v: number): [number, number, number, number] | null {
if (!this.loaded) return null
const x = Math.floor(u * (this.image.width - 1))
const y = Math.floor((1 - v) * (this.image.height - 1))
return this.getPixel(x, y)
}
public getPixel(x: number, y: number): [number, number, number, number] {
const result: [number, number, number, number] = [0, 0, 0, 0]
result[0] = this.textureData.data[((y * this.image.width + x) * 4) + 0]
result[1] = this.textureData.data[((y * this.image.width + x) * 4) + 1]
result[2] = this.textureData.data[((y * this.image.width + x) * 4) + 2]
result[3] = this.textureData.data[((y * this.image.width + x) * 4) + 3]
return result
}
}// scr/core/raster.ts
this.textureNormal = new Texture("african_head_nm.png")
this.textureDiffuse = new Texture("african_head_diffuse.png") 值得注意的是,因为使用canvas对图片进行的解码,因为的canvas解码的特性,原点在左上角,而我们的uv坐标的原点在左下角,所以对v坐标进行一个反转。
有了对于纹理贴图,在片元阶段,通过三个顶点的uv插值计算像素的uv坐标,从贴图纹理中采样其颜色值。
public fragmentShader(barycentric: Vec3): [number, number, number, number] {
const u = this.textureVetex[0].x * barycentric.x + this.textureVetex[1].x * barycentric.y + this.textureVetex[2].x * barycentric.z
const v = this.textureVetex[0].y * barycentric.x + this.textureVetex[1].y * barycentric.y + this.textureVetex[2].y * barycentric.z
const corlor = this.raster.textureDiffuse.sampling(u, v)
const normalColor = this.raster.textureNormal.sampling(u, v)
let lightIntensity = 1
if (normalColor && corlor) {
const normal = new Vec3(normalColor[0] * 2 / 255 - 1, normalColor[1] * 2 / 255 - 1, normalColor[2] * 2 / 255 - 1).normalize()
lightIntensity = Vec3.dot(Vec3.neg(this.raster.lightDir).normalize(), normal)
return [corlor[0] * lightIntensity, corlor[1] * lightIntensity, corlor[2] * lightIntensity, corlor[3]]
} else {
return [255, 255, 255, 255]
}
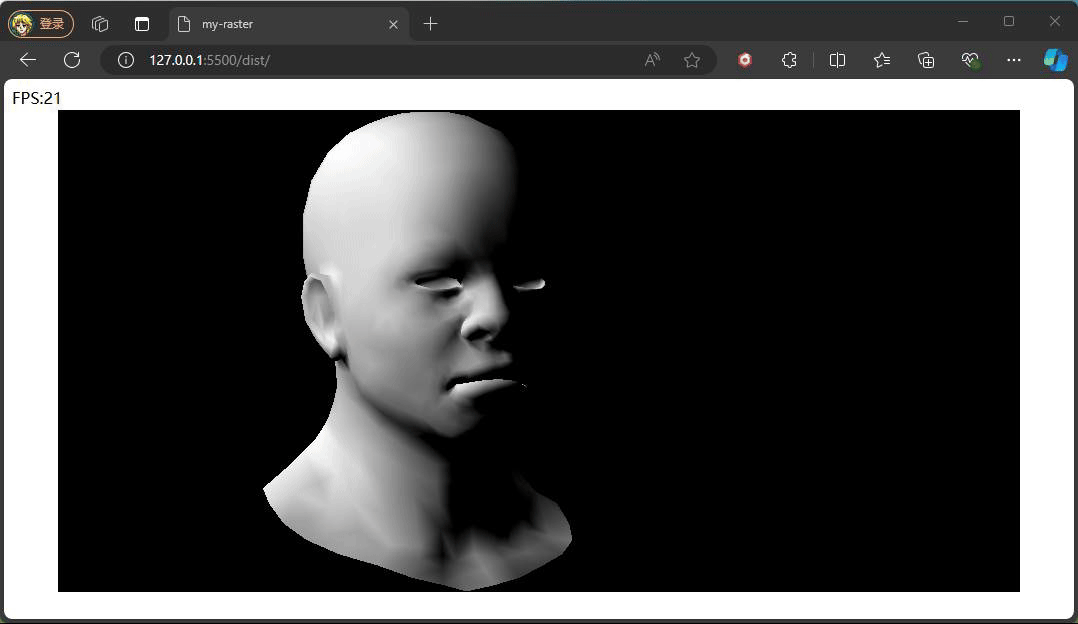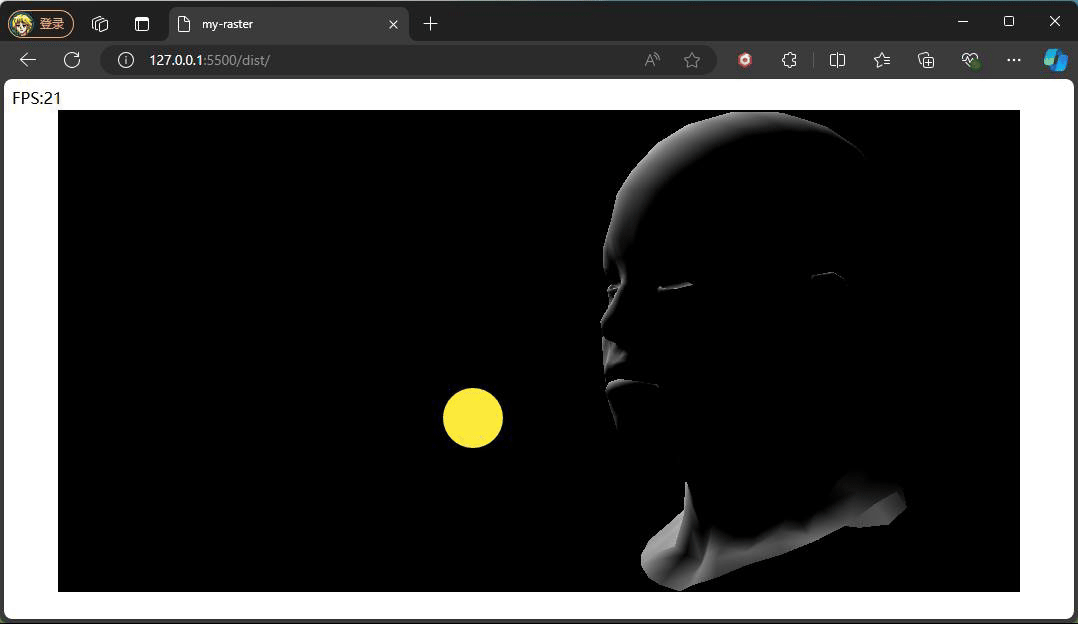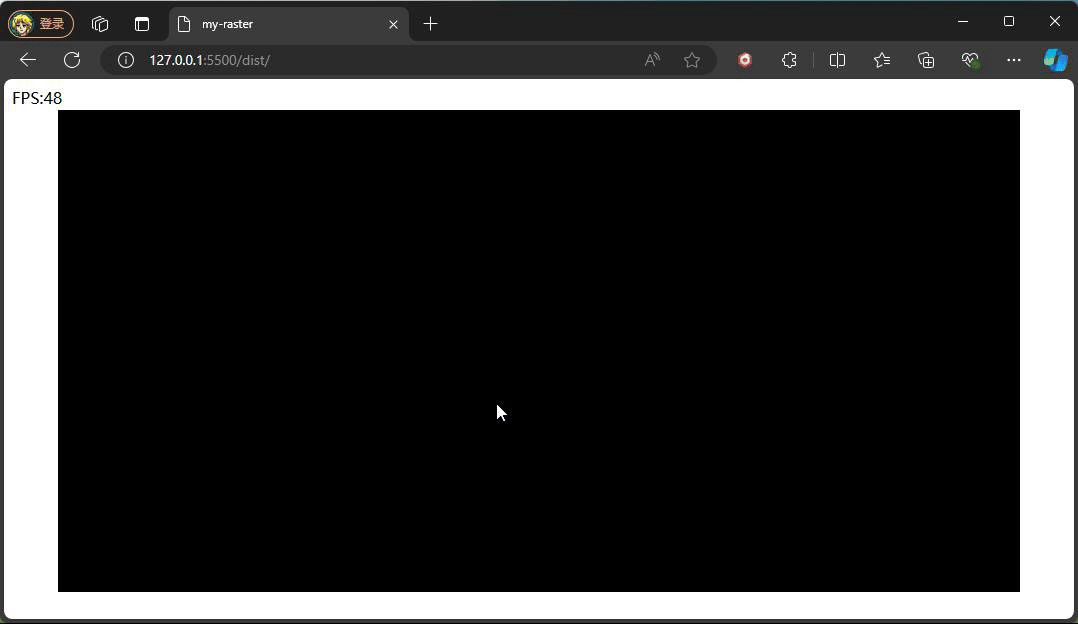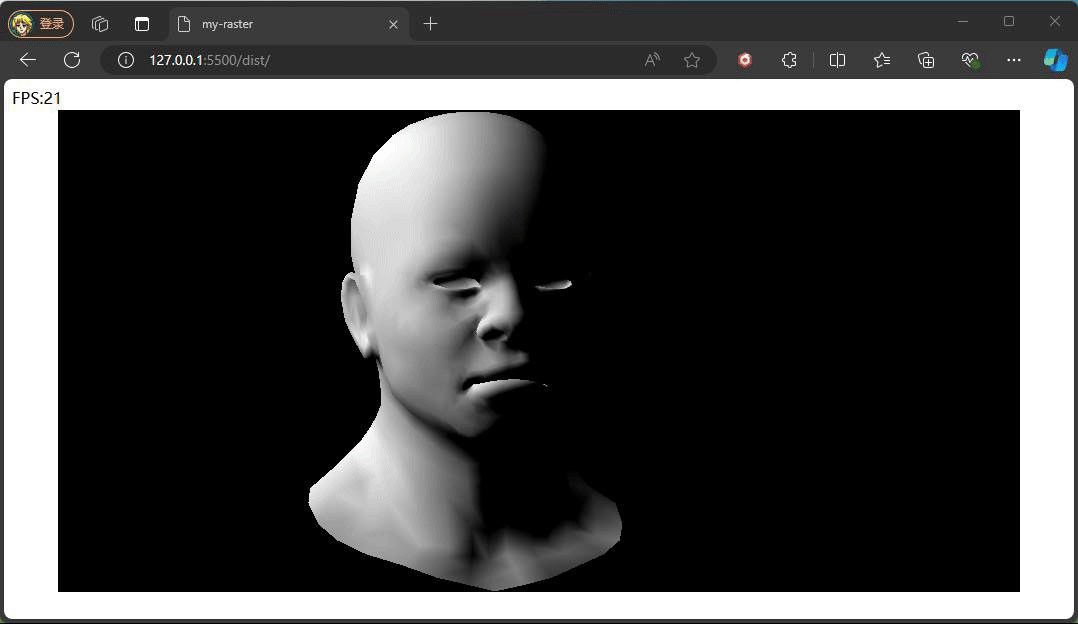
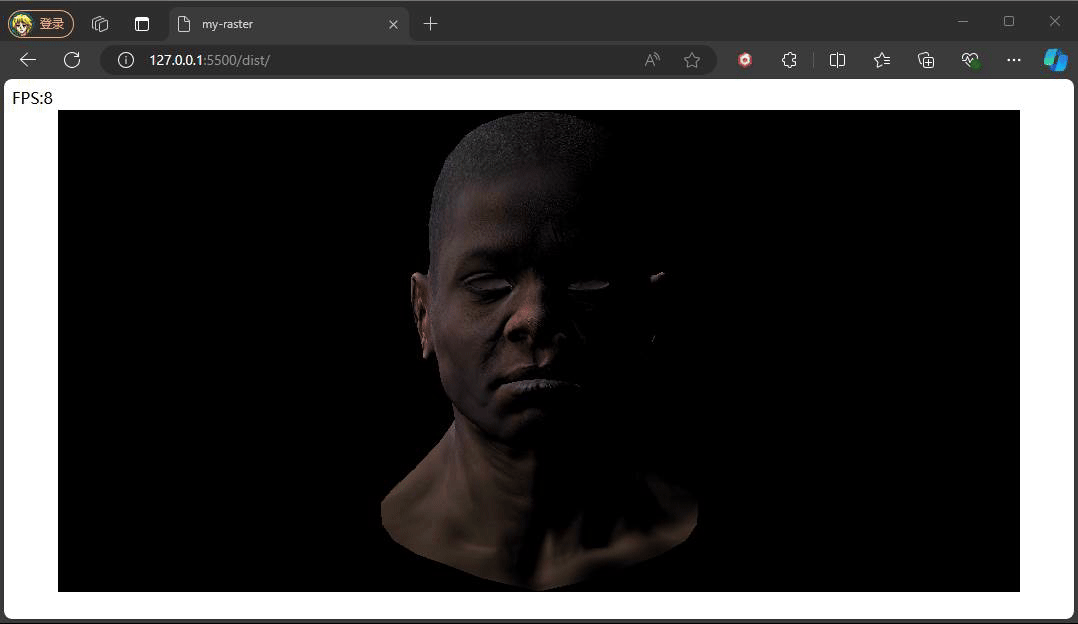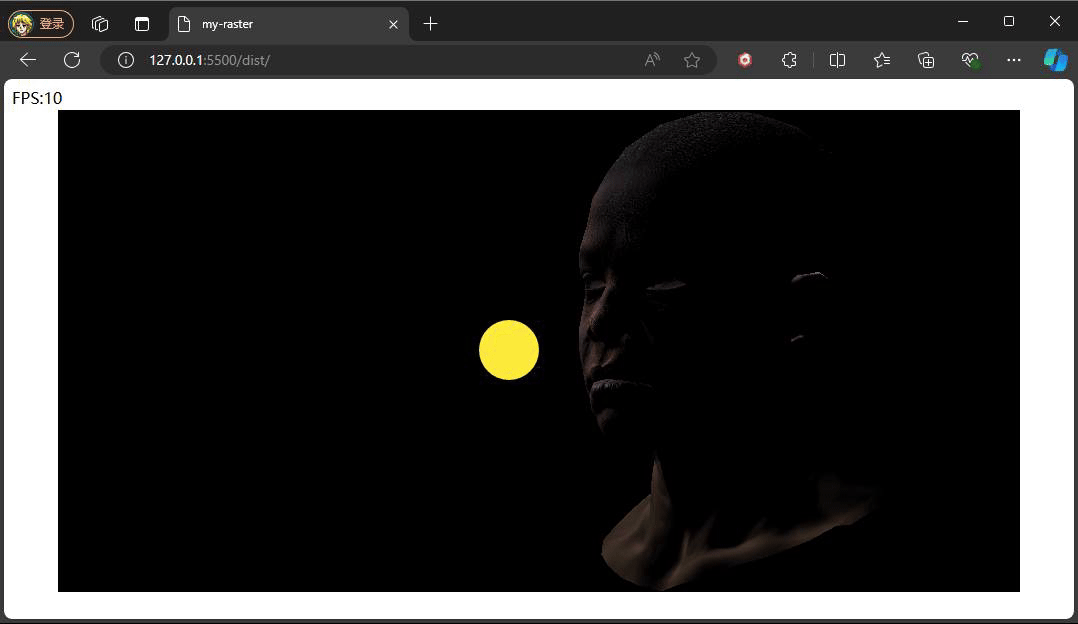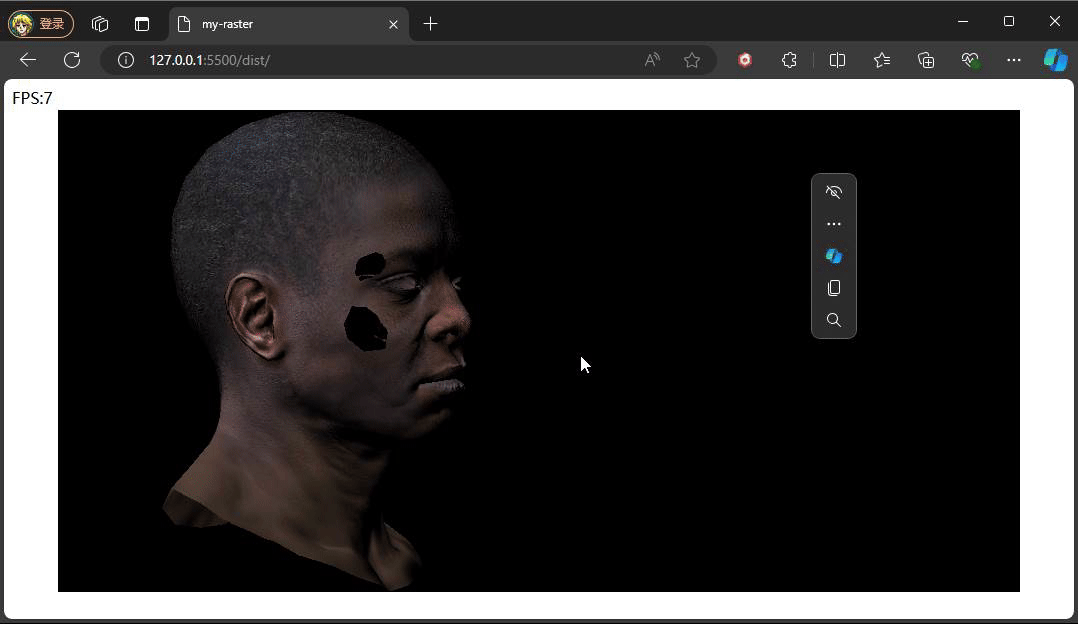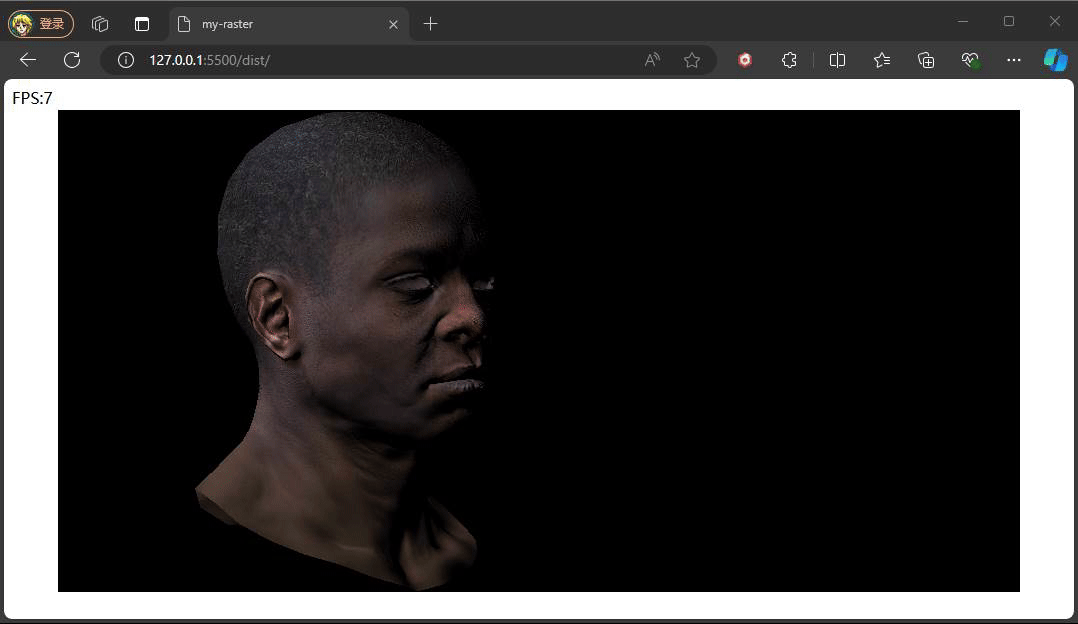
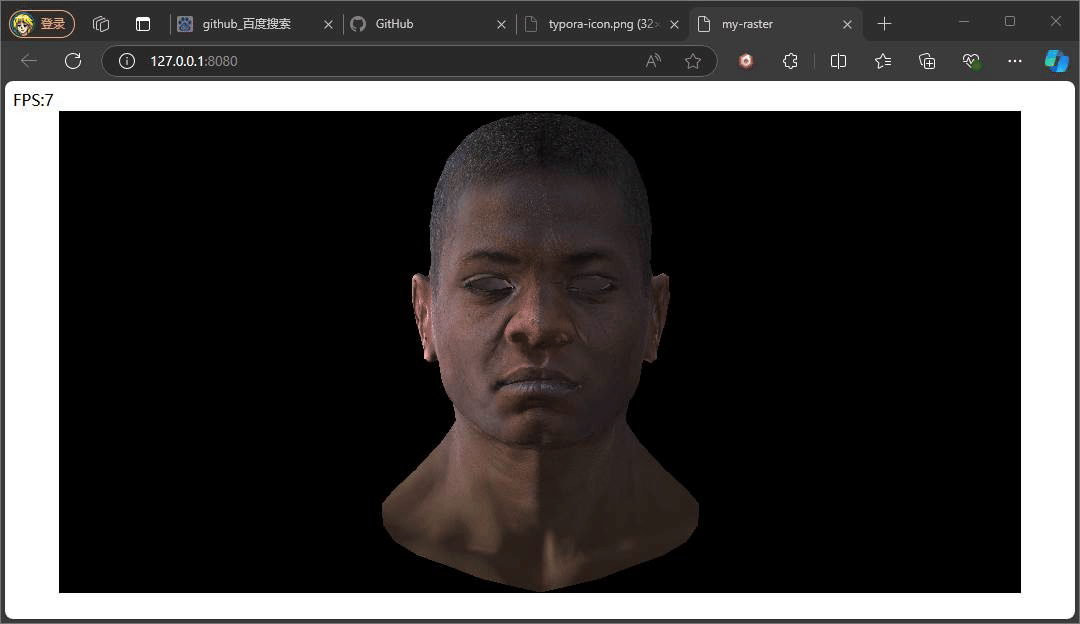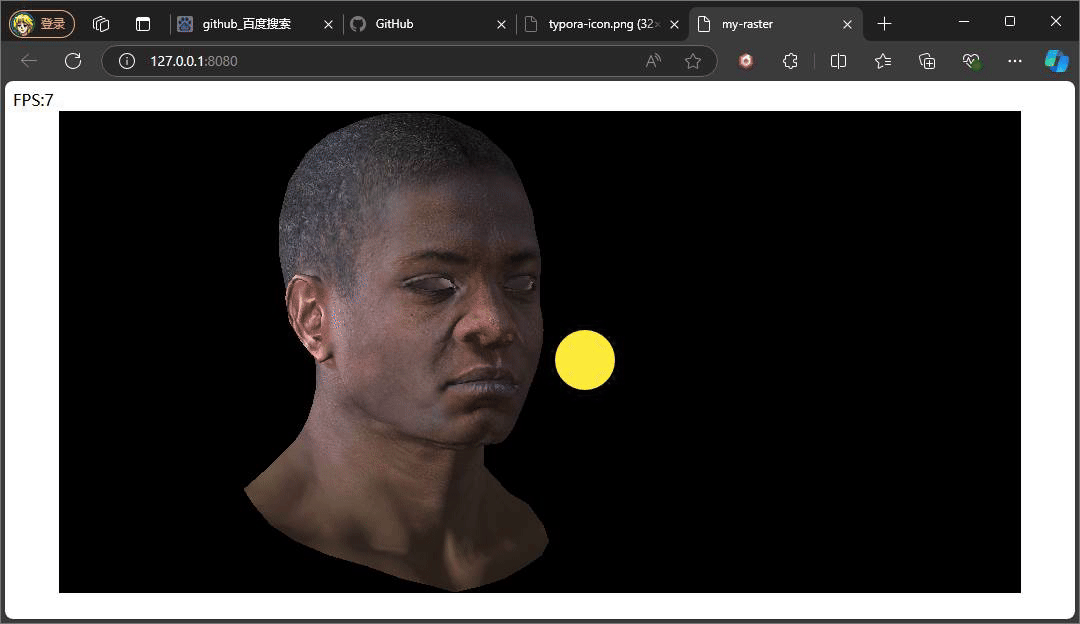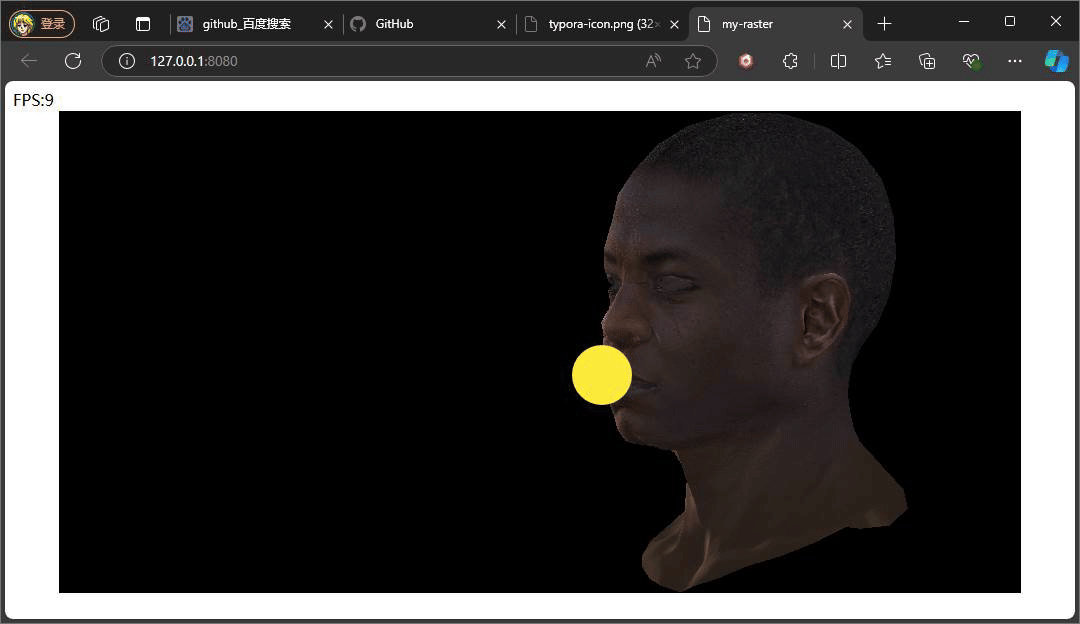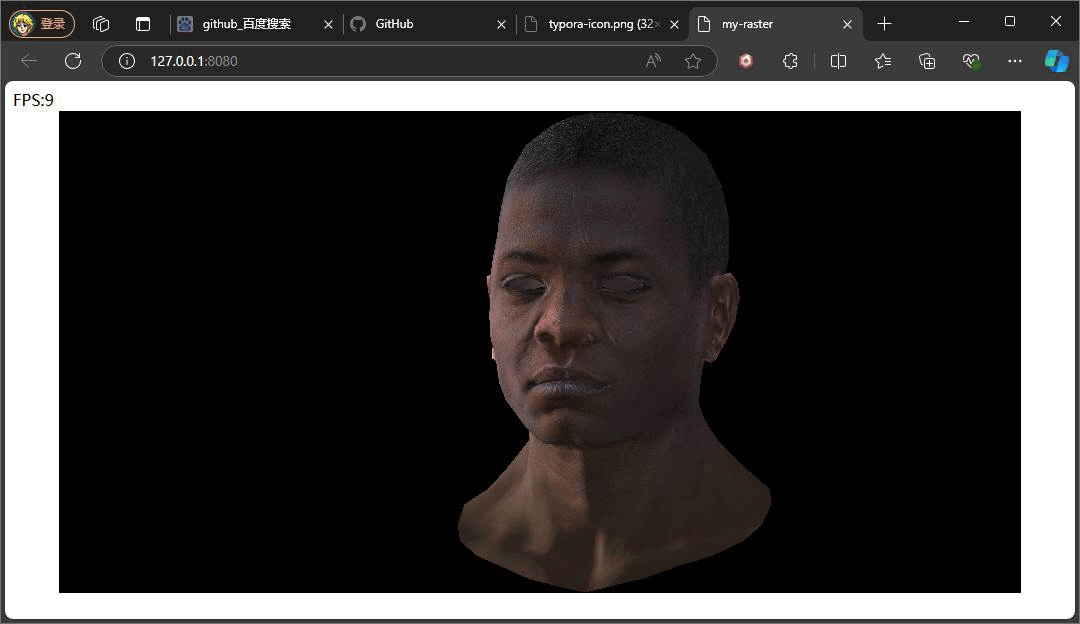
} 只要对前面用到的PhoneShading的fragmentShader中,参与光照强度计算的默认白色替换成我们从贴图获取的的颜色即可,这里对normalColor和corlor同时判断,原因和前面提交一样,纹理异步加载的,可能还未完成加载。看下效果:
未完待续。。。
光照强度在实际计算时,为遵从物理定律,需要考虑点面距离光光源的距离,距离远近所能接受的光的能量是不同,下面的光照不考虑距离,感兴趣可以自行深入补充
书接上文,从不同着色频率的角度对模型进行着色,在着色模型上只是简单采用了一种简单平行光,但是对于一个成熟的着色模型来说,只考虑一种所谓平行光是不完整的,所以本节开始介绍一个完整的着色模型所需要计算的关照,本项目着色模型实现基于phone光照模型,当然还有一个Blinn-Phong光照模型,俩者区别在于高光上计算有优化。
首先需要明确的一件事,之所以物体能被我们观察,是因为人眼接收到了从物体来的光,这些来自物体的光有很多类型,具体类型依据所使用的光照模型。基于phone光照模型,该模型定义三种光,环境光、漫反射光、高光。
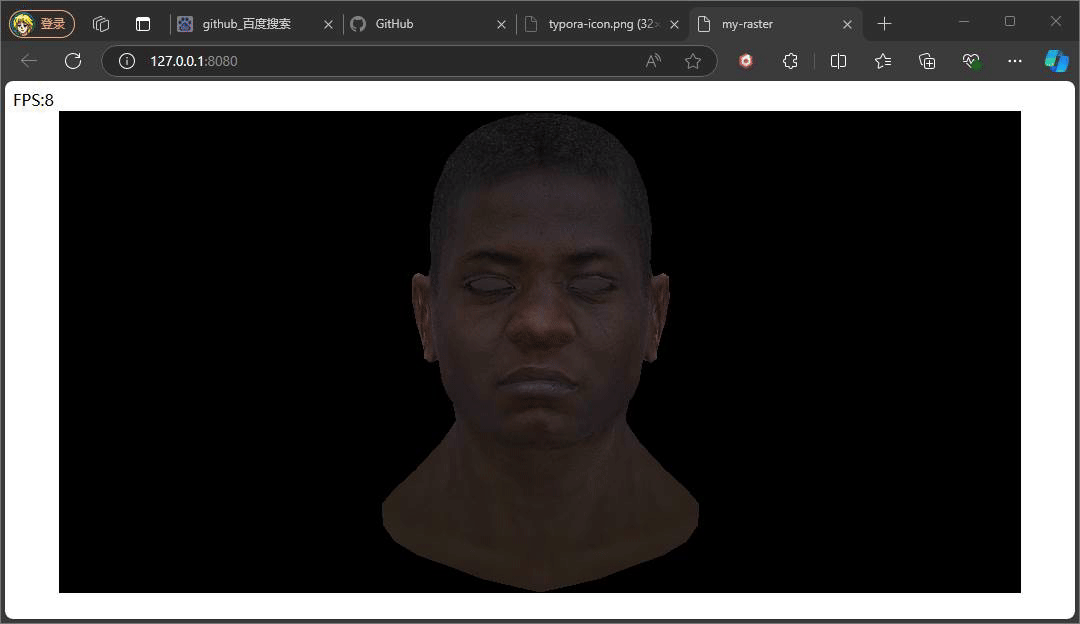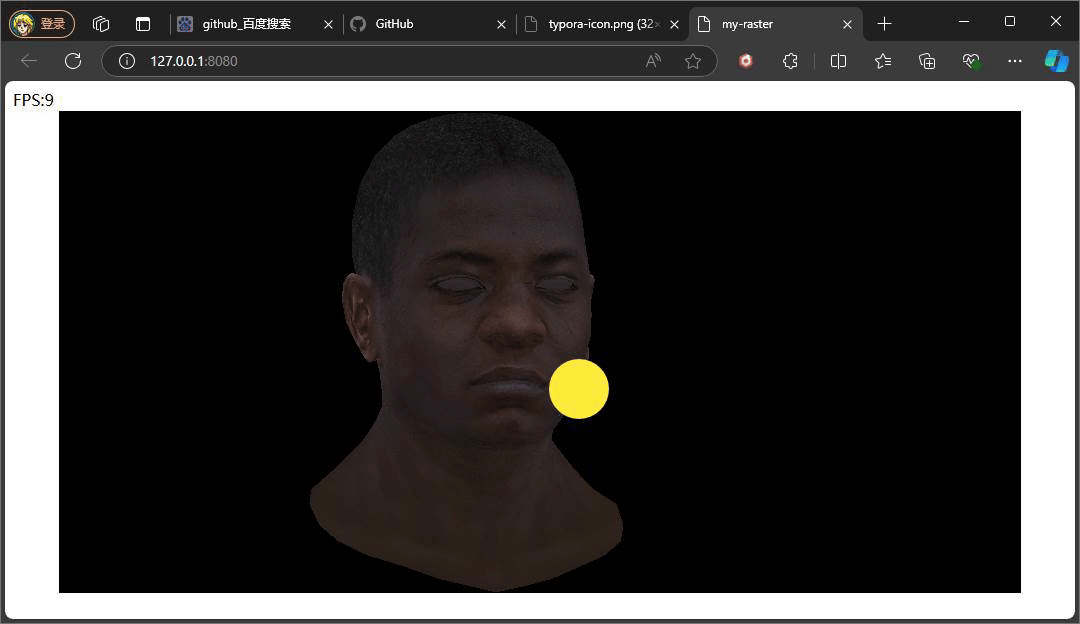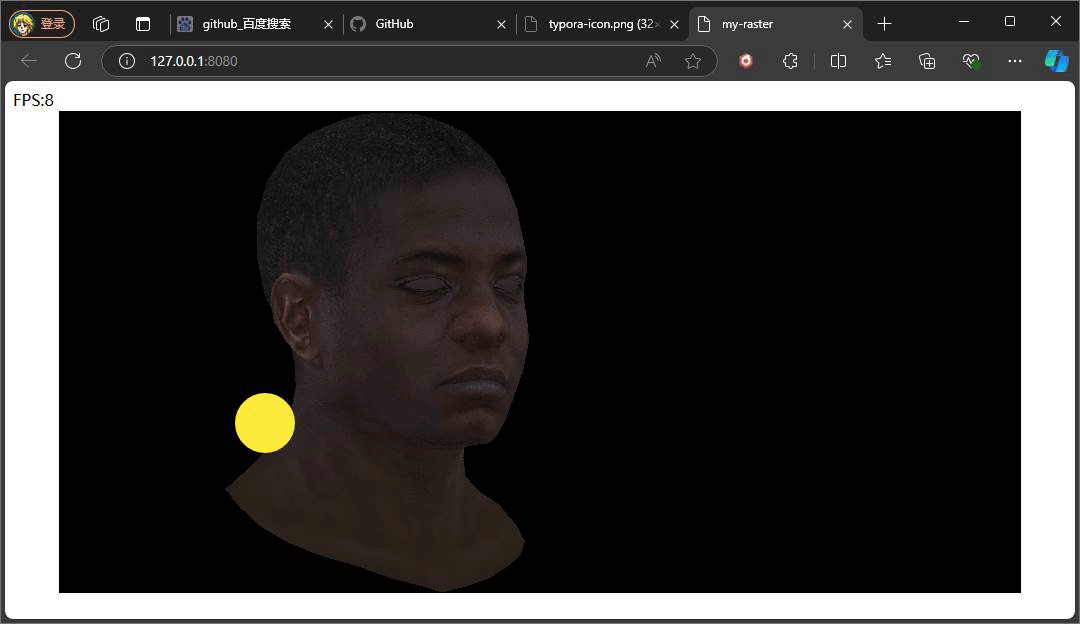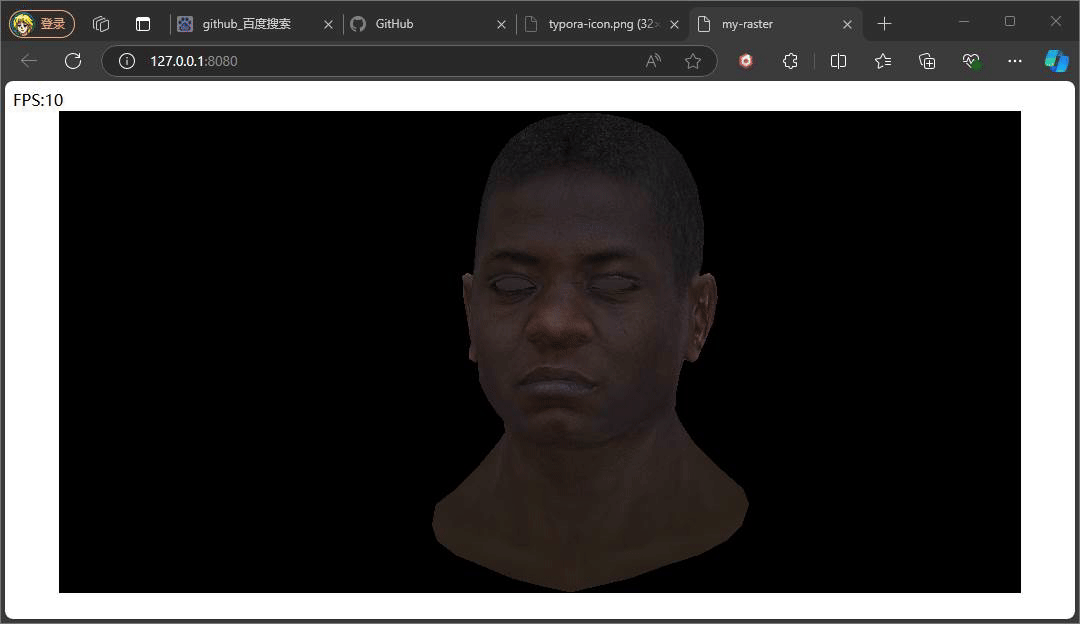
在现实环境中,周围光的折射射是复杂的,如物体背光的一面也是可能接受一定来自结果多次折射的光,并反射出去。这就是所谓的环境光,在phone光照模型中,只会去考虑环境光的影响,并且不会去精确的描述,而只是用一个简单的式子表示
其中Ka代表物体表面对环境光的反射率,Ia代表入射环境光的亮度,Ienv存储结果,即人眼所能看到从物体表面反射的环境光的亮度。
export class PhoneShader extends Shader {
public fragmentShader(barycentric: Vec3): [number, number, number, number] {
const u = this.textureVetex[0].x * barycentric.x + this.textureVetex[1].x * barycentric.y + this.textureVetex[2].x * barycentric.z
const v = this.textureVetex[0].y * barycentric.x + this.textureVetex[1].y * barycentric.y + this.textureVetex[2].y * barycentric.z
const corlor = this.raster.textureDiffuse.sampling(u, v)
const normals = this.raster.textureNormal.sampling(u, v)
if (!corlor || !normals) return [255, 255, 255, 255]
// 环境光
//const ambient = 1
const ambient = 0.5
const intensity = ambient
return [corlor[0] * intensity, corlor[1] * intensity, corlor[2] * intensity, corlor[3]]
}
} 上述俩个示意效果便是俩种不同Ienv下的结果
漫反射便是光从一定角度入射之后从入射点向四面八方反射,且每个不同方向反射的光的强度相等。决定反射光强度由光的入射方向和点面的法向量的夹角。这里的光的入射方向取决于不同类型的光源,如下:
- 平行光:光照入射角度是固定的
- 点光源:点面到光源点所形成的向量
- 聚光灯:有范围的平行光
此项目光源使用最简单的光平行光,光的入射的角度的是固定。因为涉及到点面法向量计算,所以此处法向量的计算依赖当前使用的着色频率。此处我们在逐像素频率着色实现漫反射,且平行光方向为(5,0,0):
export class PhoneShader extends Shader {
public fragmentShader(barycentric: Vec3): [number, number, number, number] {
const u = this.textureVetex[0].x * barycentric.x + this.textureVetex[1].x * barycentric.y + this.textureVetex[2].x * barycentric.z
const v = this.textureVetex[0].y * barycentric.x + this.textureVetex[1].y * barycentric.y + this.textureVetex[2].y * barycentric.z
const corlor = this.raster.textureDiffuse.sampling(u, v)
const normals = this.raster.textureNormal.sampling(u, v)
if (!corlor || !normals) return [255, 255, 255, 255]
// 环境光
const ambient = 0.5
// 漫反射
const light = Vec3.neg(this.raster.lightDir).normalize()
const diffuse = Math.max(Vec3.dot(normal, light), 0)
const intensity = ambient + diffuse
return [corlor[0] * intensity, corlor[1] * intensity, corlor[2] * intensity, corlor[3]]
}
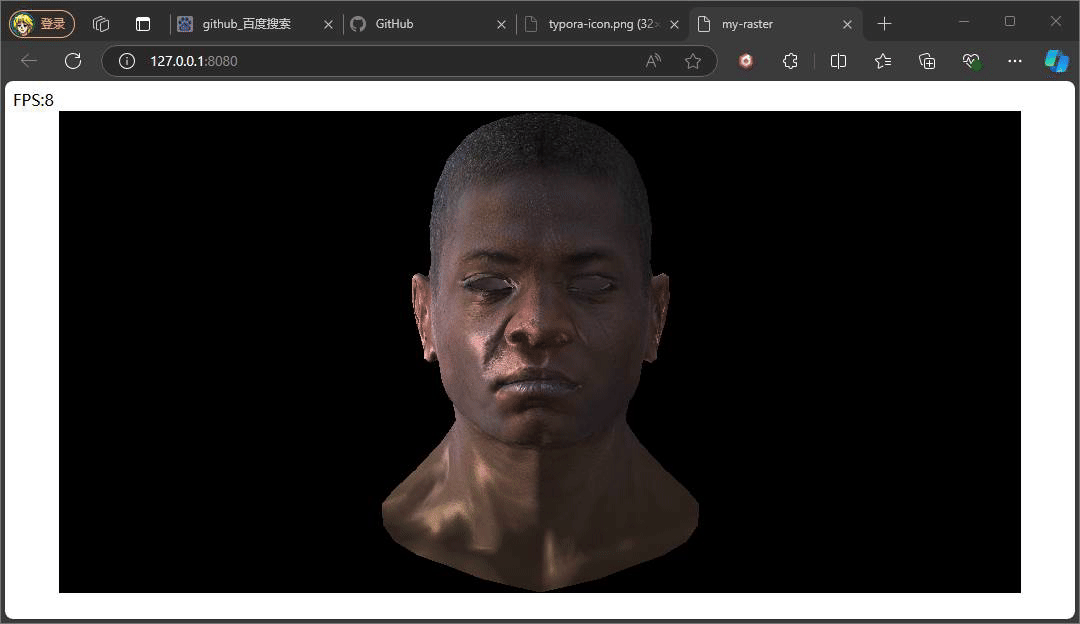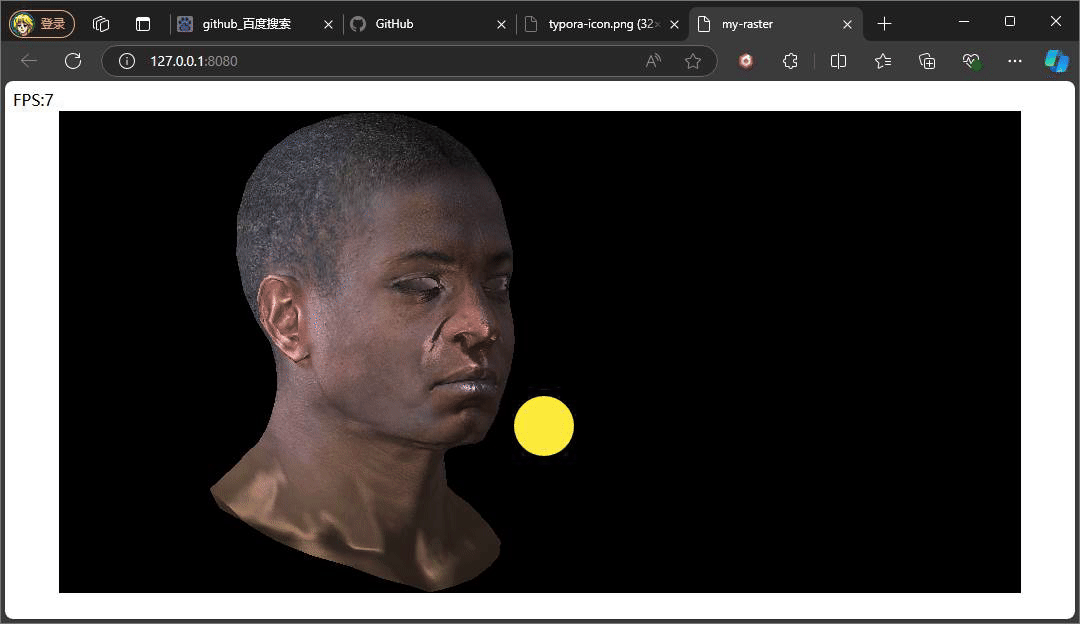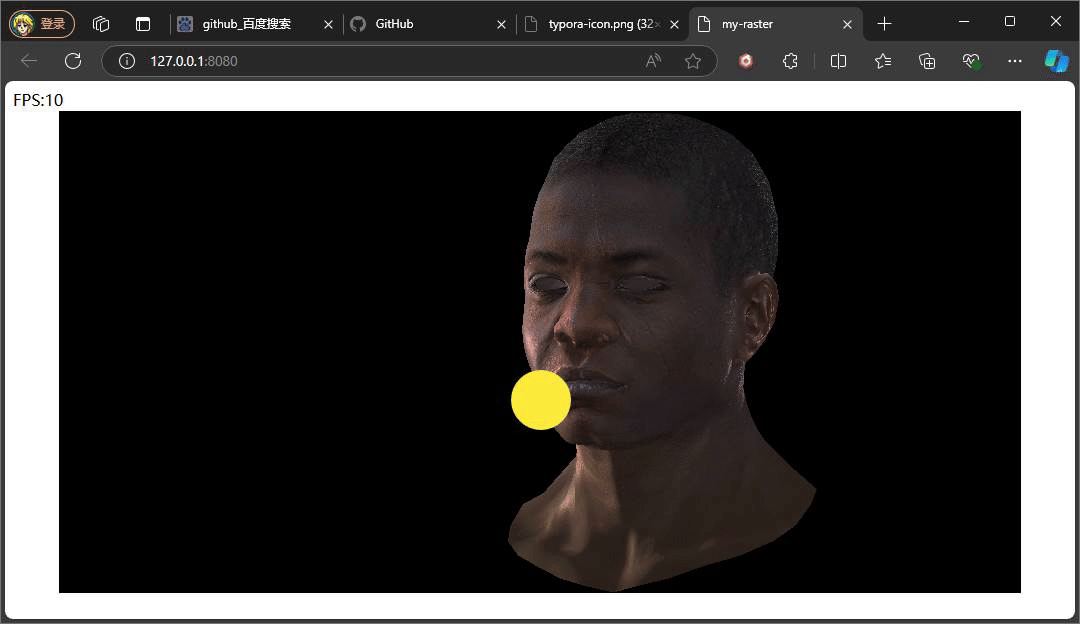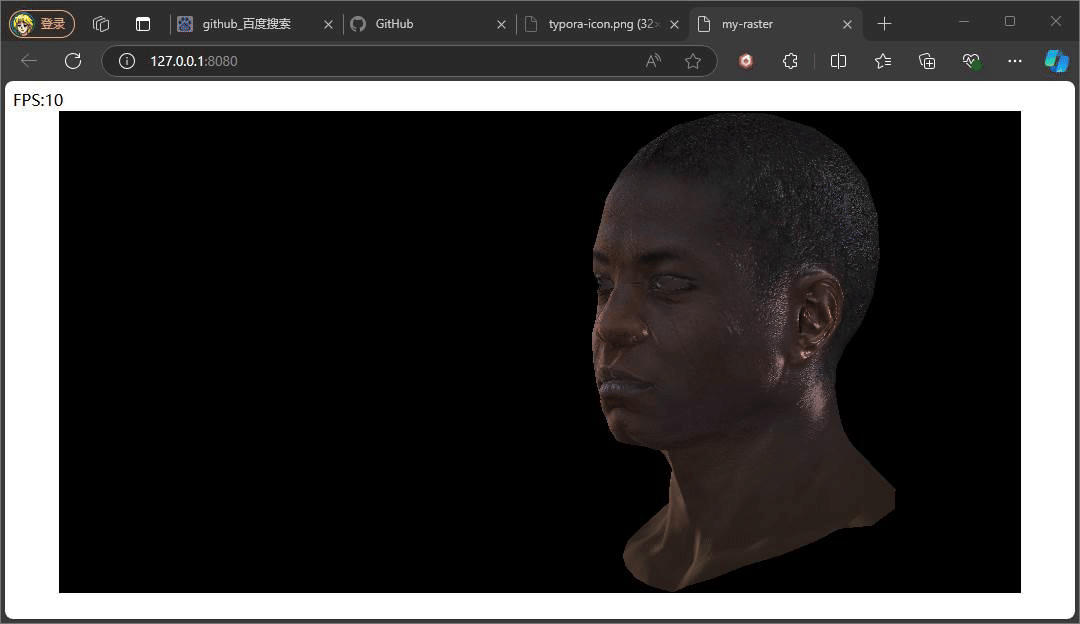
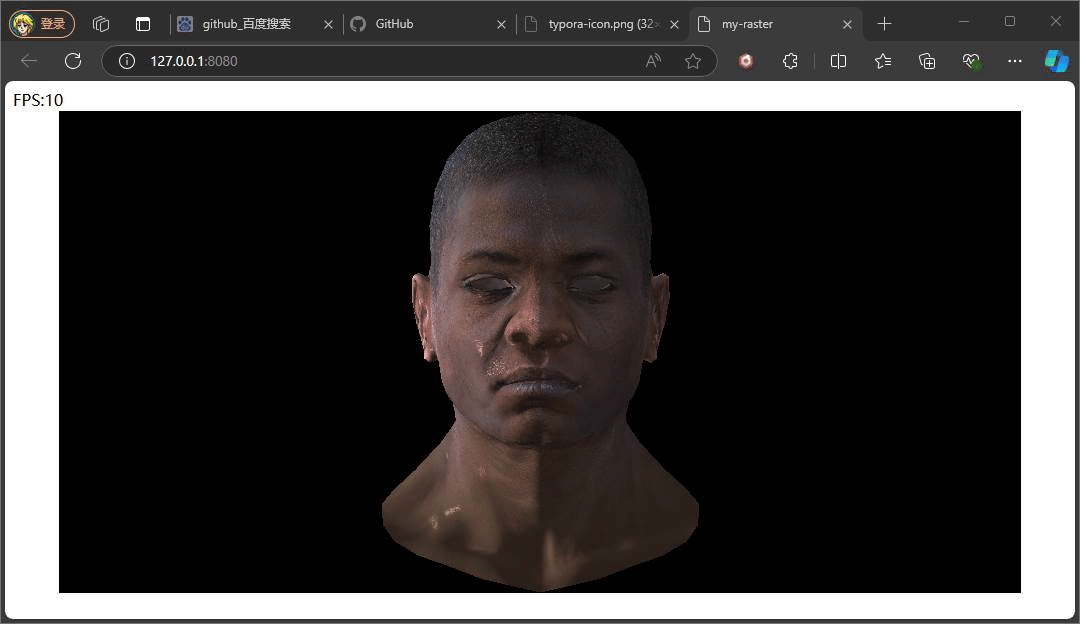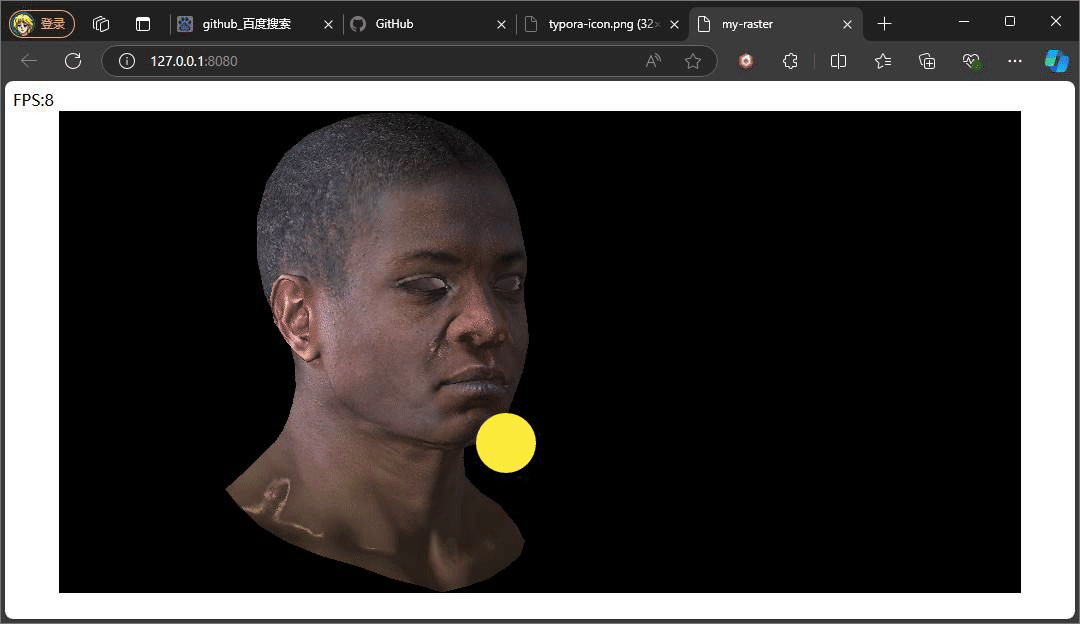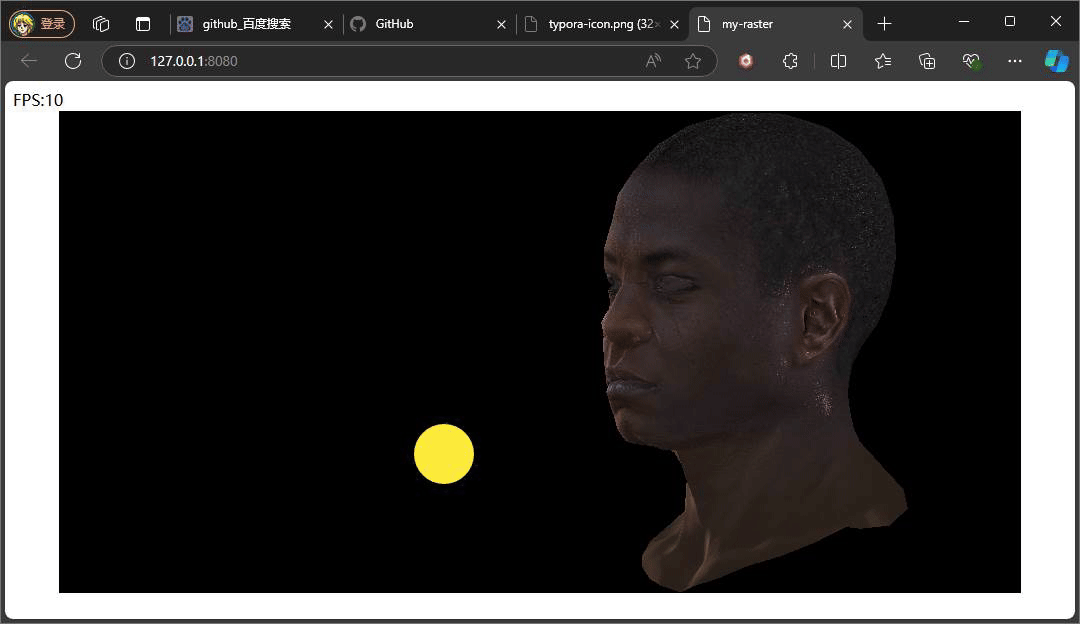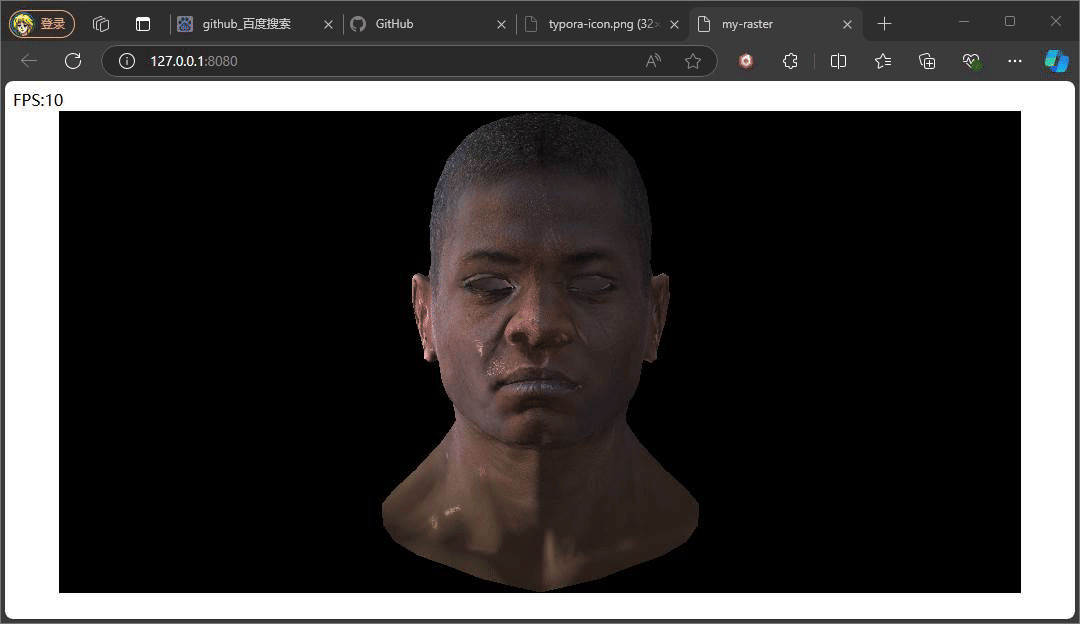
} 上述效果便是叠加的环境光和漫反射光所展示出来的,平行光方向朝X的正半轴,所以左侧脸部亮度明显比右侧更亮,因为环境光的存在,即使位于右侧脸部也有着一定的着色亮度。
该光故名思意,物体会反射光,当发射光刚好到达观察方向,此时会出现高光部分,如现实生活中的镜子。所以高光的出现取决于观察方向,和反射光方向。也就是反射方向和观察方向的夹角:
const u = this.textureVetex[0].x * barycentric.x + this.textureVetex[1].x * barycentric.y + this.textureVetex[2].x * barycentric.z
const v = this.textureVetex[0].y * barycentric.x + this.textureVetex[1].y * barycentric.y + this.textureVetex[2].y * barycentric.z
const x = this.viewSpaceVertex[0].x * barycentric.x + this.viewSpaceVertex[1].x * barycentric.y + this.viewSpaceVertex[2].x
const y = this.viewSpaceVertex[0].y * barycentric.x + this.viewSpaceVertex[1].y * barycentric.y + this.viewSpaceVertex[2].y
const z = this.viewSpaceVertex[0].z * barycentric.x + this.viewSpaceVertex[1].z * barycentric.y + this.viewSpaceVertex[2].z
const corlor = this.raster.textureDiffuse.sampling(u, v)
const normals = this.raster.textureNormal.sampling(u, v)
if (!corlor || !normals) return [255, 255, 255, 255]
const light = Vec3.neg(this.raster.lightDir).normalize()
const normal = new Vec3(normals[0] * 2 / 255 - 1, normals[1] * 2 / 255 - 1, normals[2] * 2 / 255 - 1).normalize()
// 环境光
const ambient = .5
// 漫反射
const diffuse = Math.max(Vec3.dot(normal, light), 0)
// 镜面反射
const reflect = normal.scale(2 * Vec3.dot(normal, light)).sub(light)
const viewVec = new Vec3(0, 0, 0).sub(new Vec3(x, y, z)).normalize()
const specular = Math.pow(Math.max(Vec3.dot(reflect, viewVec), 0), 32)
const intensity = ambient + diffuse + specular
return [corlor[0] * intensity, corlor[1] * intensity, corlor[2] * intensity, corlor[3]]
}
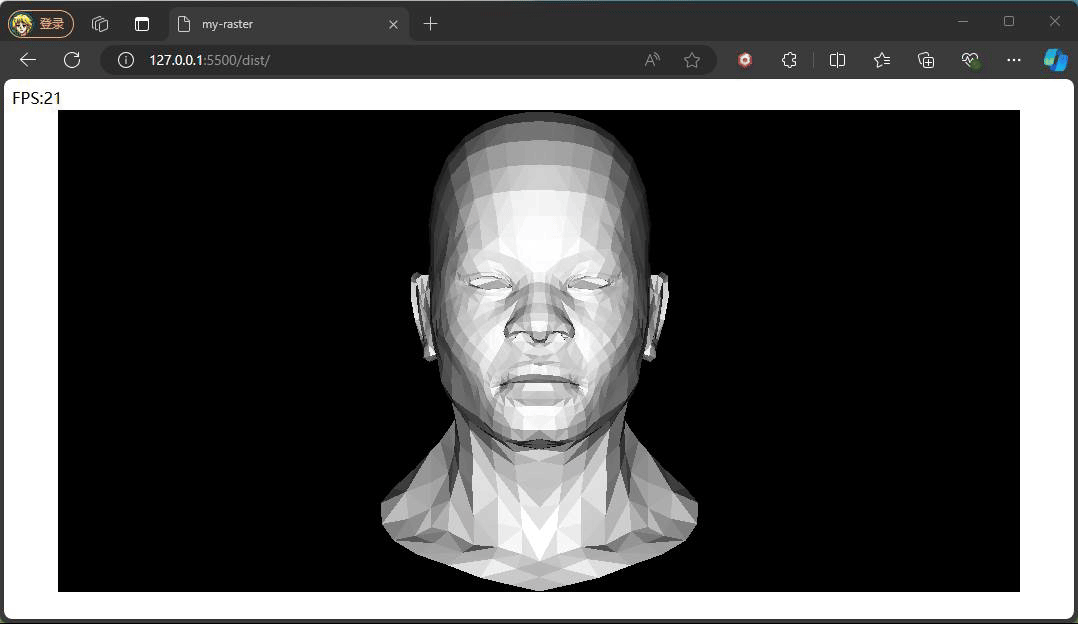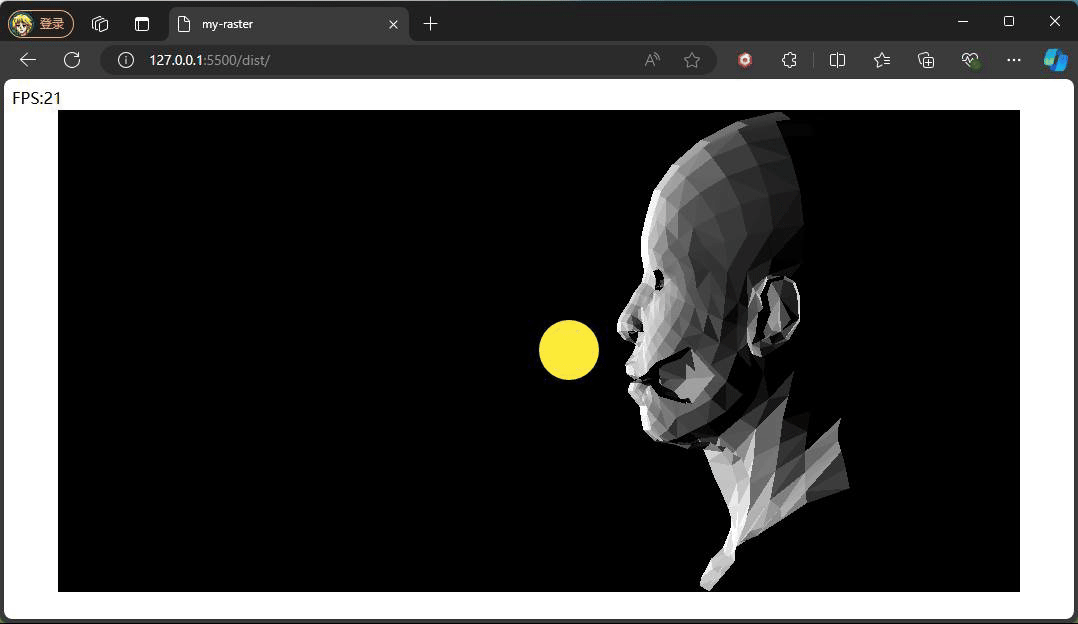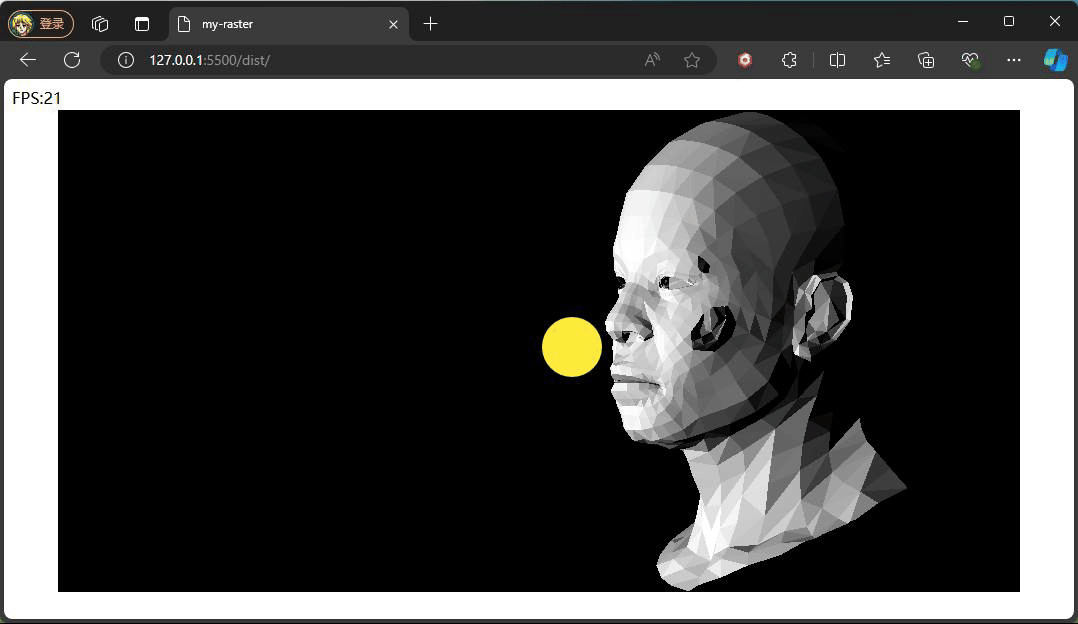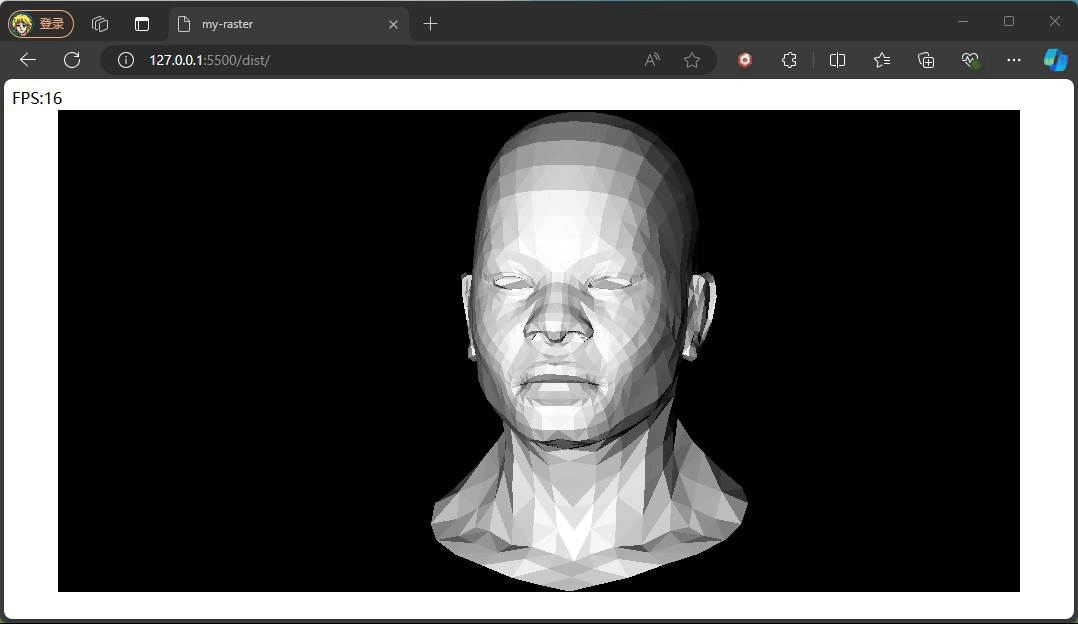
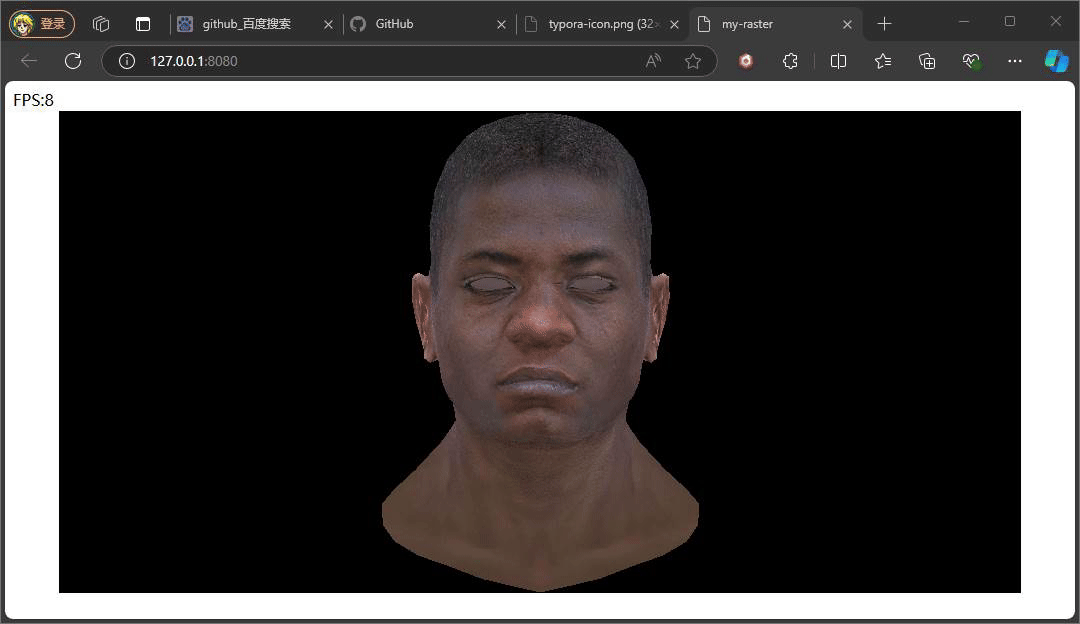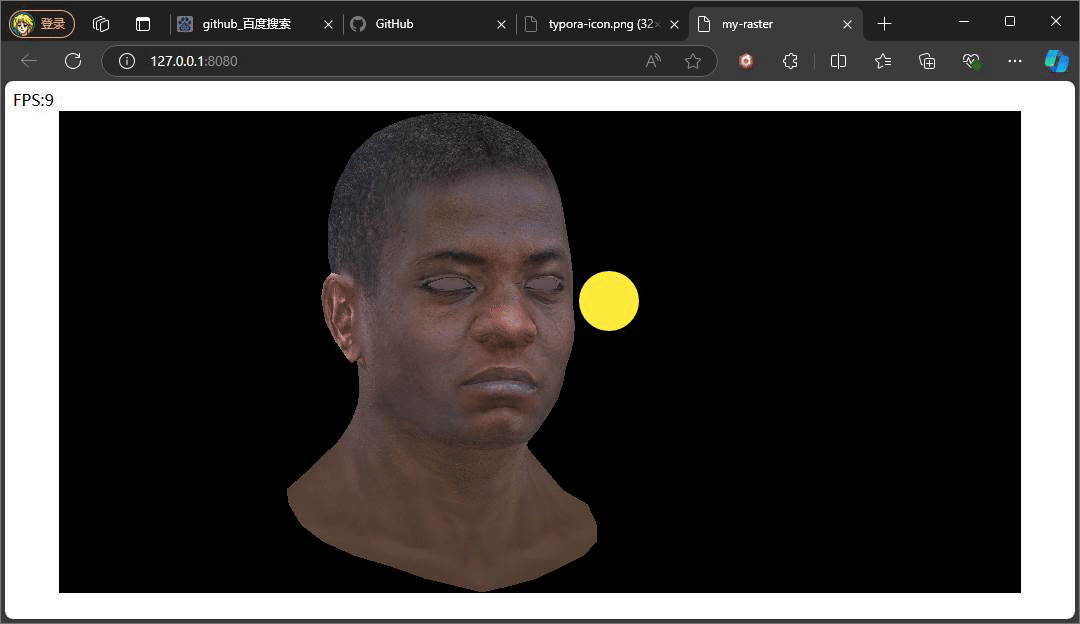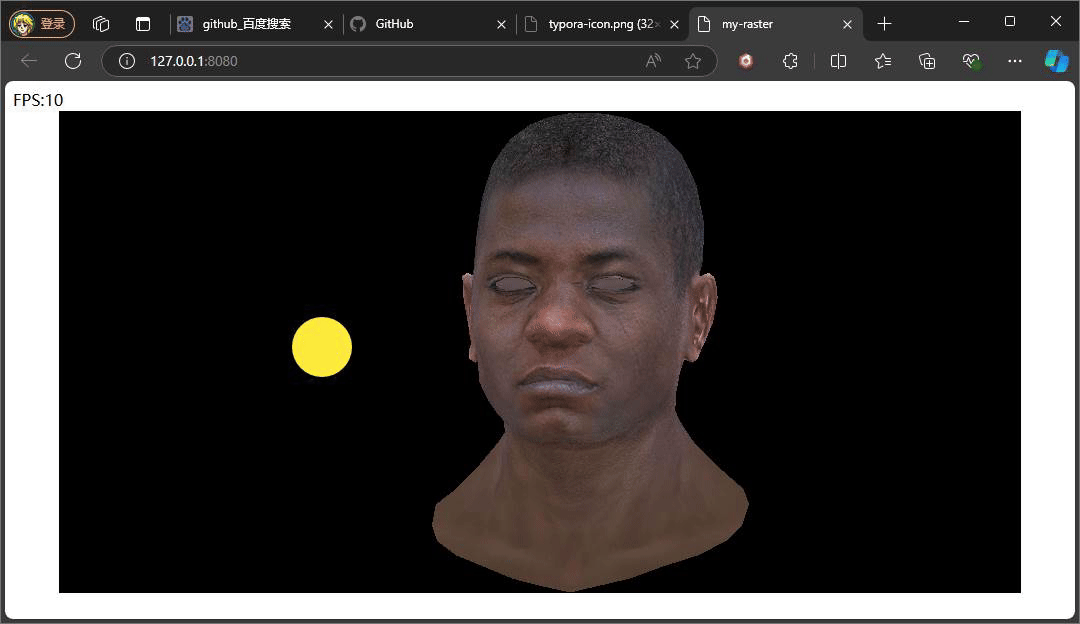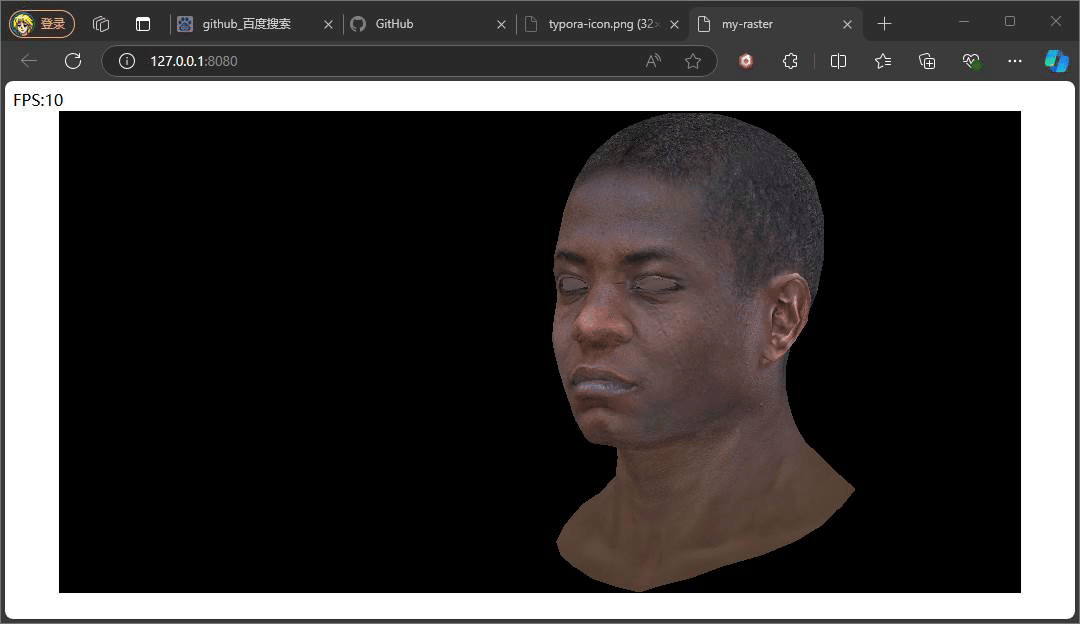
} 此处的反射光的方向是一个固定公式,参考phone光照模型,入射光采用的是平行光,固定的入射角度。重点是观察方向,观察方向是该点面到观察(相机)位置所形成的向量,注意此处通过插值计算当前该像素的世界坐标,继而将世界坐标转换成视图空间下的坐标,因为在视图空间下,相机位置便就是原点。最后通过一个p系数次方来控制高光的范围,这个值通常也会从一种高光贴图中采取。
上述俩种不同结果,就是通过调整系数P,来控制高光的范围大小,值得注意的是,当我们旋转相机时,高光的位置也在发生变化,即使我们相机的位置没有发生变化,但是通过旋转物体相对相机的位置是在变化,也就是转换到视图空间下,物体坐标发生了变化,又因为高光中观察方向是由物体的点面到观察方向所形成的向量,这也是为什么上述提及计算观察方向时,将插值得到的世界坐标转换到视图空间下的坐标。
- 上次更新:24.9.16
- 未完待续