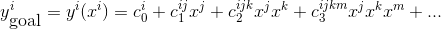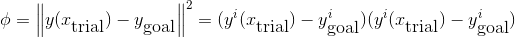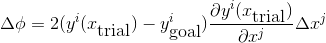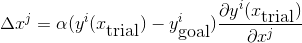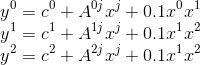-
Notifications
You must be signed in to change notification settings - Fork 0
Home
This header-only library provides a basic Gradient Descent iterative solver for nonlinear algebraic systems of equations. There are some nonlinear computational modeling problems that can be formulated as a system of equations with linear and nonlinear (i.e: multinomial) terms in the unknowns. This problem appears often when trying to obtaining solutions to nonlinear Finite Element problems, nonlinear Spectral methods and nonlinear semi-Espectral element methods.
A nonlinear algebraic system can be written as the following system of equations:
Where the convention of sum over repeated indices is assumed. To obtain a solution, we will provide a trial vector, and evaluate the scalar function
if our trial vector were a solution to the algebraic system, the scalar phi would evaluate to zero. phi is always positive, and it has global minima in all the solutions. If we evaluate the change in phi provided by a change in the trial vector, we consider such an increment as
the optimal decrement of phi will be given by
Where alpha is some negative factor. Ideally, we obtain the optimal step alpha by evaluating error bounds given by second derivative terms. In practice, it might be cheaper to do a small linear search around the point to find an optimal decrement.
In the iterative solver test, you can see examples of usage. Basically, you need to provide a template class that will load all the coefficients (linear and nonlinear) of the system, and pass an instance of it to the solver constructor
template <typename ValueType, unsigned int Order, unsigned int RankX, unsigned int RankY, bool MakeNonLinear= false>
struct Poly2LoaderExample
{
void load_array( typename MD<ValueType, RankY + Order*RankX >::RegArray& arr)
{
}
Poly2LoaderExample< ValueType, Order-1 , RankX , RankY> subloader;
};Template polymorphism is a type of duck polymorphism (if it quacks, it is a duck). Basically a loader template class is valid as long as it provides a load_array method for the multidimensional array of the appropiate rank, and if it provides an instance of the loader for the subranks called subloader.
Given the above template, we provide specializations for each rank of the cofficients of the problem:
template <typename ValueType>
struct Poly2LoaderExample< ValueType, 0 , 1 , 1>
{
void load_array( typename MD<ValueType, 1 >::RegArray& arr)
{
arr.assign( _Index({ 0}) , ValueType(-5.0));
arr.assign( _Index({ 1}) , ValueType(5.0));
arr.assign( _Index({ 2}) , ValueType(2.0));
}
};
template <typename ValueType>
struct Poly2LoaderExample< ValueType, 1 , 1 , 1>
{
void load_array( typename MD<ValueType, 2 >::RegArray& arr)
{
arr.assign( _Index({ 0, 0}) , ValueType(1.0));
arr.assign( _Index({ 0, 1}) , ValueType(0.5));
arr.assign( _Index({ 0, 2}) , ValueType(8.0));
arr.assign( _Index({ 1, 0}) , ValueType(0.5));
arr.assign( _Index({ 1, 1}) , ValueType(-3.0));
arr.assign( _Index({ 1, 2}) , ValueType(5.0));
arr.assign( _Index({ 2, 0}) , ValueType(8.0));
arr.assign( _Index({ 2, 1}) , ValueType(5.0));
arr.assign( _Index({ 2, 2}) , ValueType(3.2));
}
Poly2LoaderExample< ValueType, 0 , 1 , 1> subloader;
};
template <typename ValueType, bool MakeNonLinear>
struct Poly2LoaderExample< ValueType, 2 , 1 , 1, MakeNonLinear>
{
void load_array( typename MD<ValueType, 3 >::RegArray& arr)
{
if (MakeNonLinear)
{
arr.assign( _Index({ 0, 0, 1}) , ValueType(0.1));
arr.assign( _Index({ 1, 1, 2}) , ValueType(0.1));
arr.assign( _Index({ 2, 2, 1}) , ValueType(0.1));
}
}
Poly2LoaderExample< ValueType, 1 , 1 , 1> subloader;
};We pass the makeNonLinear boolean parameter as a convenience to enable or disable the nonlinear terms for testing.
As you see, the linear matrix (rank 2) coefficients are symmetric. This is usually the case that the base linear problem is Hermitian. On the 2-order specialization, we add the following nonlinear coefficients
We now instantiate the object and provide the vector of goal values. We can leave it empty, which is interpreted as equal to zero everywhere:
MD< double , 1 >::RegArray y_goal;
Poly2LoaderExample< double, 2 , 1 , 1 , true> nonlinearSymmetricLoader;
AlgebraicIterativeSolver< double , 2 , 1 , 1 > ais_nonlinear(nonlinearSymmetricLoader, y_goal);now we pass a trial vector (note that the trial vector object is passed by pointer, not value, so it will be modified in place).
MD< double , 1 >::RegArray x_test;
x_test.assign( _Index({0}) , 9.1 );
x_test.assign( _Index({1}) , -3.1 );
x_test.assign( _Index({2}) , -10.2 );
ais_2_nonlinear.setCurrentXTest(x_test);We won't discuss much what kind of heuristics should go in good trial vector values, suffice to say that we might want to consider the problem without the nonlinear terms first, and use the linear solution as a seed for the full nonlinear problem.
Now we only need to iterate the solver until the phi is as close enough to zero as we want:
int iterations = 500;
double phi = 1.0;
do
{
phi = ais_2_nonlinear.line_search_update();
} while (phi > 1e-10 && (iterations-- > 0));