Replies: 4 comments
-
|
There are two separate issues here: (1) the meaning of term marginal test, and (2) redundancy of the interaction term. Marginal tests study the effect of the term when it is removed from the model containing all other terms. In interaction model The second issue is that the interaction term is redundant. In the first ( It seems that both of your terms have 1 degree of freedom. This implies that they have only two levels (two types of |
Beta Was this translation helpful? Give feedback.
-
|
So If I understand correctly, in the default mode(terms) the interaction host:feces_host does not add anything new to the model and that is why it is removed and only appears host and feces_host. I was worried because when I saw the example: I think that I get it know. Thank you very much for the quick response! Ps: Yes I have two types of hosts and feces_host |
Beta Was this translation helpful? Give feedback.
-
|
About that F =−∞: The F is based on zero change in sum of squares with zero degrees of freedom, and it will involve term 0/0 so that the result should strictly be |
Beta Was this translation helpful? Give feedback.
-
|
Hello, again I have another doubt about interpreting R2 Values when using the byterm or bymargin mode. Following with the above example, imaging that I have "host" and "feces_host" variables and I repeat the adonis2 byterm or bymargin with only one variable. Would the resulting R2 values be comparable? For example, Would be the the variance that "host" explains by its own > than "feces_host"? |
Beta Was this translation helpful? Give feedback.
-
Hello,
I have a Aitchison distance matrix (CLR Transformation+Euclidean distance), called temp_d, derived from 16S based data. I have various groups, and I wanted to analyze their variables with a PERMANOVA for feces transplant. The variables shown are host(species from which the samples were obtained), and feces_host (species form which the input feces came from). I have try both default, by term, and by margin, but I need help to understand the results.
When using by margin:

When using including interactions(*) in the model formula, only the interaction term appears and F statistic=-Inf (I don't understand the meaning of this -Inf for the F statistic), but not the individual terms. However when I do it using only interactions(:), or only terms(+), it works, but not when terms and interactions are both included in the model.
When using the default:
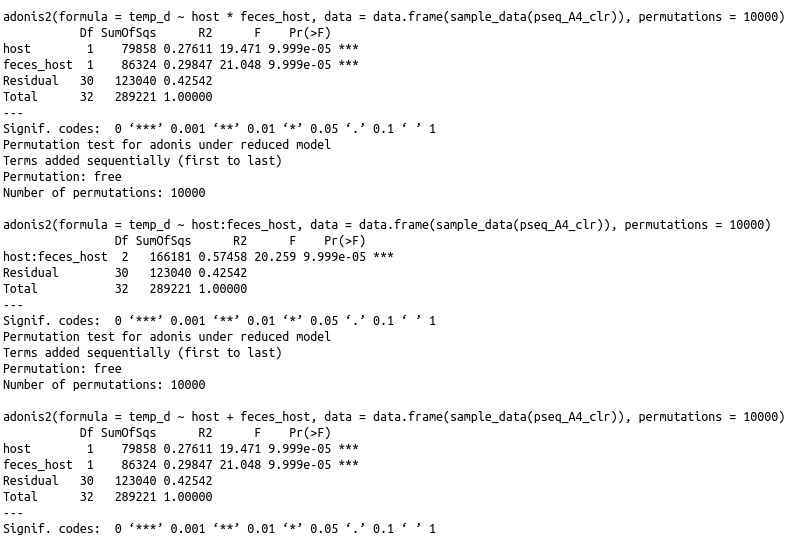
When using including interactions(*) in the model formula, only the terms appear, but not the interaction term, being the result identical to use only (+). However when I do it using only interactions(:), or only terms(+), it works, but not when terms and interactions are both included in the model.
Thanks in advance for any help!
Beta Was this translation helpful? Give feedback.
All reactions