| layout | title | sched-activation |
|---|---|---|
course |
Week 7, Wednesday (February 26, 2014) |
class="active" |
Our system model (Takada, Chap. 2)
- Nodes run independently
- No shared memory or shared clock
- Network may reorder or lose messages
- Nodes can fail but do not have bugs and cannot be hacked
- Handling buggy or hacked nodes imposes even more overhead (see Byzantine fault tolerance)
Implications
-
A node only has fast access to its own state
-
Global time order cannot be observed
- From the system's perspective, there is no global order unless the system enforces one
- Global information is potentially out of date or inconsistent
-
Crashes differ from network partitions
- A crashed node cannot update
- A partitioned node can update
- A node on the other side of the partition cannot tell if updates are occurring inside it
Nodes achieve consensus if they all agree on some value, such as:
- Value of an entry that two nodes have updated
- Ordering of actions performed by several nodes
- Completion of a shared action
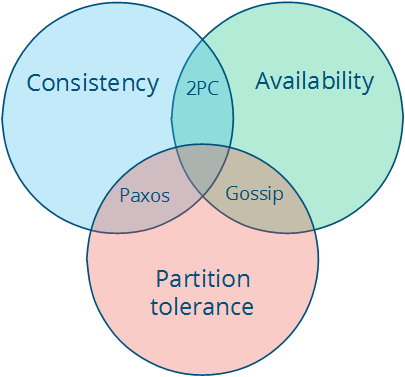
Brewer's CAP "Theorem" (2000): Consistency, availability, partition tolerance---pick any two:
Source: {{site.data.bibliography.takada2013.title}}, Ch. 2. Note: Paxos, Two-phase commit (2PC), and Gossip are algorithms
Not really a theorem
-
More an argument to expand the design space
-
Can't choose to have availability without partition tolerance
- If your system stops at a partition, it is unavailable
-
There are many kinds of consistency
-
You will make different tradeoffs for different services in a system:
- Fine to be off by one on count of Twitter followers for Beyoncé
- Not so fine to book two weddings in the same room the same time
- Consider compensation methods
-
Seth Gilbert and Nancy Lynch proved a specific case of CAP Theorem
- But their assumptions do not apply to all systems
- More in their 2012 article
Read {{site.data.bibliography.takada2013.title}}, from "A system model", up to but not including "Strong consistency vs. other consistency models".
You can skim:
- The formal definition of the consensus problem
- The section, "The FLP impossibility result"
The key points:
- Different assumptions about what can fail and how it can fail
- How those assumptions can make algorithms simpler or more complicated
- The zones of the CAP Venn diagram