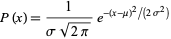|
The answers here are given by the community. Be careful and double check the answers before using them. If you see an error, please create a PR with a fix |
- The list of questions is based on this post
- Legend: 👶 easy ⭐️ medium 🚀 expert
- Do you know how to answer questions without answers? Please create a PR
What is supervised machine learning? 👶
A case when we have both features (the matrix X) and the labels (the vector y)
What is regression? Which models can you use to solve a regression problem? 👶
Regression is a part of supervised ML. Regression models investigate the relationship between a dependent (target) and independent variable (s) (predictor). Here are some common regression models
- Linear Regression establishes a linear relationship between target and predictor (s). It predicts a numeric value and has a shape of a straight line.
- Polynomial Regression has a regression equation with the power of independent variable more than 1. It is a curve that fits into the data points.
- Ridge Regression helps when predictors are highly correlated (multicollinearity problem). It penalizes the squares of regression coefficients but doesn’t allow the coefficients to reach zeros (uses L2 regularization).
- Lasso Regression penalizes the absolute values of regression coefficients and allows some of the coefficients to reach absolute zero (thereby allowing feature selection).
What is linear regression? When do we use it? 👶
Linear regression is a model that assumes a linear relationship between the input variables (X) and the single output variable (y).
With a simple equation:
y = B0 + B1*x1 + ... + Bn * xN
B is regression coefficients, x values are the independent (explanatory) variables and y is dependent variable.
The case of one explanatory variable is called simple linear regression. For more than one explanatory variable, the process is called multiple linear regression.
Simple linear regression:
y = B0 + B1*x1
Multiple linear regression:
y = B0 + B1*x1 + ... + Bn * xN
What are the main assumptions of linear regression? ⭐
There are several assumptions of linear regression. If any of them is violated, model predictions and interpretation may be worthless or misleading.
- Linear relationship between features and target variable.
- Additivity means that the effect of changes in one of the features on the target variable does not depend on values of other features. For example, a model for predicting revenue of a company have of two features - the number of items a sold and the number of items b sold. When company sells more items a the revenue increases and this is independent of the number of items b sold. But, if customers who buy a stop buying b, the additivity assumption is violated.
- Features are not correlated (no collinearity) since it can be difficult to separate out the individual effects of collinear features on the target variable.
- Errors are independently and identically normally distributed (yi = B0 + B1*x1i + ... + errori):
- No correlation between errors (consecutive errors in the case of time series data).
- Constant variance of errors - homoscedasticity. For example, in case of time series, seasonal patterns can increase errors in seasons with higher activity.
- Errors are normaly distributed, otherwise some features will have more influence on the target variable than to others. If the error distribution is significantly non-normal, confidence intervals may be too wide or too narrow.
What’s the normal distribution? Why do we care about it? 👶
The normal distribution is a continuous probability distribution whose probability density function takes the following formula:
where μ is the mean and σ is the standard deviation of the distribution.
The normal distribution derives its importance from the Central Limit Theorem, which states that if we draw a large enough number of samples, their mean will follow a normal distribution regardless of the initial distribution of the sample, i.e the distribution of the mean of the samples is normal. It is important that each sample is independent from the other.
This is powerful because it helps us study processes whose population distribution is unknown to us.
How do we check if a variable follows the normal distribution? ⭐️
- Plot a histogram out of the sampled data. If you can fit the bell-shaped "normal" curve to the histogram, then the hypothesis that the underlying random variable follows the normal distribution can not be rejected.
- Check Skewness and Kurtosis of the sampled data. Skewness = 0 and kurtosis = 3 are typical for a normal distribution, so the farther away they are from these values, the more non-normal the distribution.
- Use Kolmogorov-Smirnov or/and Shapiro-Wilk tests for normality. They take into account both Skewness and Kurtosis simultaneously.
- Check for Quantile-Quantile plot. It is a scatterplot created by plotting two sets of quantiles against one another. Normal Q-Q plot place the data points in a roughly straight line.
What if we want to build a model for predicting prices? Are prices distributed normally? Do we need to do any pre-processing for prices? ⭐️
Data is not normal. Specially, real-world datasets or uncleaned datasets always have certain skewness. Same goes for the price prediction. Price of houses or any other thing under consideration depends on a number of factors. So, there's a great chance of presence of some skewed values i.e outliers if we talk in data science terms.
Yes, you may need to do pre-processing. Most probably, you will need to remove the outliers to make your distribution near-to-normal.
What methods for solving linear regression do you know? ⭐️
To solve linear regression, you need to find the coefficients which minimize the sum of squared errors.
Matrix Algebra method: Let's say you have X, a matrix of features, and y, a vector with the values you want to predict. After going through the matrix algebra and minimization problem, you get this solution: .
But solving this requires you to find an inverse, which can be time-consuming, if not impossible. Luckily, there are methods like Singular Value Decomposition (SVD) or QR Decomposition that can reliably calculate this part (called the pseudo-inverse) without actually needing to find an inverse. The popular python ML library
sklearn uses SVD to solve least squares.
Alternative method: Gradient Descent. See explanation below.
What is gradient descent? How does it work? ⭐️
Gradient descent is an algorithm that uses calculus concept of gradient to try and reach local or global minima. It works by taking the negative of the gradient in a point of a given function, and updating that point repeatedly using the calculated negative gradient, until the algorithm reaches a local or global minimum, which will cause future iterations of the algorithm to return values that are equal or too close to the current point. It is widely used in machine learning applications.
What is the normal equation? ⭐️
Normal equations are equations obtained by setting equal to zero the partial derivatives of the sum of squared errors (least squares); normal equations allow one to estimate the parameters of a multiple linear regression.
What is SGD — stochastic gradient descent? What’s the difference with the usual gradient descent? ⭐️
In both gradient descent (GD) and stochastic gradient descent (SGD), you update a set of parameters in an iterative manner to minimize an error function.
While in GD, you have to run through ALL the samples in your training set to do a single update for a parameter in a particular iteration, in SGD, on the other hand, you use ONLY ONE or SUBSET of training sample from your training set to do the update for a parameter in a particular iteration. If you use SUBSET, it is called Minibatch Stochastic gradient Descent.
Which metrics for evaluating regression models do you know? 👶
- Mean Squared Error(MSE)
- Root Mean Squared Error(RMSE)
- Mean Absolute Error(MAE)
- R² or Coefficient of Determination
- Adjusted R²
What are MSE and RMSE? 👶
MSE stands for Mean Square Error while RMSE stands for Root Mean Square Error. They are metrics with which we can evaluate models.
What is the bias-variance trade-off? 👶
Bias is the error introduced by approximating the true underlying function, which can be quite complex, by a simpler model. Variance is a model sensitivity to changes in the training dataset.
Bias-variance trade-off is a relationship between the expected test error and the variance and the bias - both contribute to the level of the test error and ideally should be as small as possible:
ExpectedTestError = Variance + Bias² + IrreducibleError
But as a model complexity increases, the bias decreases and the variance increases which leads to overfitting. And vice versa, model simplification helps to decrease the variance but it increases the bias which leads to underfitting.
What is overfitting? 👶
When your model perform very well on your training set but can't generalize the test set, because it adjusted a lot to the training set.
How to validate your models? 👶
One of the most common approaches is splitting data into train, validation and test parts. Models are trained on train data, hyperparameters (for example early stopping) are selected based on the validation data, the final measurement is done on test dataset. Another approach is cross-validation: split dataset into K folds and each time train models on training folds and measure the performance on the validation folds. Also you could combine these approaches: make a test/holdout dataset and do cross-validation on the rest of the data. The final quality is measured on test dataset.
Why do we need to split our data into three parts: train, validation, and test? 👶
The training set is used to fit the model, i.e. to train the model with the data. The validation set is then used to provide an unbiased evaluation of a model while fine-tuning hyperparameters. This improves the generalization of the model. Finally, a test data set which the model has never "seen" before should be used for the final evaluation of the model. This allows for an unbiased evaluation of the model. The evaluation should never be performed on the same data that is used for training. Otherwise the model performance would not be representative.
Can you explain how cross-validation works? 👶
Cross-validation is the process to separate your total training set into two subsets: training and validation set, and evaluate your model to choose the hyperparameters. But you do this process iteratively, selecting differents training and validation set, in order to reduce the bias that you would have by selecting only one validation set.
What is K-fold cross-validation? 👶
K fold cross validation is a method of cross validation where we select a hyperparameter k. The dataset is now divided into k parts. Now, we take the 1st part as validation set and remaining k-1 as training set. Then we take the 2nd part as validation set and remaining k-1 parts as training set. Like this, each part is used as validation set once and the remaining k-1 parts are taken together and used as training set. It should not be used in a time series data.
How do we choose K in K-fold cross-validation? What’s your favorite K? 👶
There are two things to consider while deciding K: the number of models we get and the size of validation set. We do not want the number of models to be too less, like 2 or 3. At least 4 models give a less biased decision on the metrics. On the other hand, we would want the dataset to be at least 20-25% of the entire data. So that at least a ratio of 3:1 between training and validation set is maintained.
I tend to use 4 for small datasets and 5 for large ones as K.
What is classification? Which models would you use to solve a classification problem? 👶
Classification problems are problems in which our prediction space is discrete, i.e. there is a finite number of values the output variable can be. Some models which can be used to solve classification problems are: logistic regression, decision tree, random forests, multi-layer perceptron, one-vs-all, amongst others.
What is logistic regression? When do we need to use it? 👶
Logistic regression is a Machine Learning algorithm that is used for binary classification. You should use logistic regression when your Y variable takes only two values, e.g. True and False, "spam" and "not spam", "churn" and "not churn" and so on. The variable is said to be a "binary" or "dichotomous".
Is logistic regression a linear model? Why? 👶
Yes, Logistic Regression is considered a generalized linear model because the outcome always depends on the sum of the inputs and parameters. Or in other words, the output cannot depend on the product (or quotient, etc.) of its parameters.
What is sigmoid? What does it do? 👶
A sigmoid function is a type of activation function, and more specifically defined as a squashing function. Squashing functions limit the output to a range between 0 and 1, making these functions useful in the prediction of probabilities.
Sigmod(x) = 1/(1+e^{-x})
How do we evaluate classification models? 👶
Depending on the classification problem, we can use the following evaluation metrics:
- Accuracy
- Precision
- Recall
- F1 Score
- Logistic loss (also known as Cross-entropy loss)
- Jaccard similarity coefficient score
What is accuracy? 👶
Accuracy is a metric for evaluating classification models. It is calculated by dividing the number of correct predictions by the number of total predictions.
Is accuracy always a good metric? 👶
Accuracy is not a good performance metric when there is imbalance in the dataset. For example, in binary classification with 95% of A class and 5% of B class, prediction accuracy can be 95%. In case of imbalance dataset, we need to choose Precision, recall, or F1 Score depending on the problem we are trying to solve.
What is the confusion table? What are the cells in this table? 👶
Confusion table (or confusion matrix) shows how many True positives (TP), True Negative (TN), False Positive (FP) and False Negative (FN) model has made.
| Actual | Actual | ||
|---|---|---|---|
| Positive (1) | Negative (0) | ||
| Predicted | Positive (1) | TP | FP |
| Predicted | Negative (0) | FN | TN |
- True Positives (TP): When the actual class of the observation is 1 (True) and the prediction is 1 (True)
- True Negative (TN): When the actual class of the observation is 0 (False) and the prediction is 0 (False)
- False Positive (FP): When the actual class of the observation is 0 (False) and the prediction is 1 (True)
- False Negative (FN): When the actual class of the observation is 1 (True) and the prediction is 0 (False)
Most of the performance metrics for classification models are based on the values of the confusion matrix.
What are precision, recall, and F1-score? 👶
- Precision and recall are classification evaluation metrics:
- P = TP / (TP + FP) and R = TP / (TP + FN).
- Where TP is true positives, FP is false positives and FN is false negatives
- In both cases the score of 1 is the best: we get no false positives or false negatives and only true positives.
- F1 is a combination of both precision and recall in one score (harmonic mean):
- F1 = 2 * PR / (P + R).
- Max F score is 1 and min is 0, with 1 being the best.
Precision-recall trade-off ⭐️
Tradeoff means increasing one parameter would lead to decreasing of other. Precision-recall tradeoff occur due to increasing one of the parameter(precision or recall) while keeping the model same.
In an ideal scenario where there is a perfectly separable data, both precision and recall can get maximum value of 1.0. But in most of the practical situations, there is noise in the dataset and the dataset is not perfectly separable. There might be some points of positive class closer to the negative class and vice versa. In such cases, shifting the decision boundary can either increase the precision or recall but not both. Increasing one parameter leads to decreasing of the other.
What is the ROC curve? When to use it? ⭐️
ROC stands for Receiver Operating Characteristics. The diagrammatic representation that shows the contrast between true positive rate vs true negative rate. It is used when we need to predict the probability of the binary outcome.
What is AUC (AU ROC)? When to use it? ⭐️
AUC stands for Area Under the ROC Curve. ROC is a probability curve and AUC represents degree or measure of separability. It's used when we need to value how much model is capable of distinguishing between classes. The value is between 0 and 1, the higher the better.
How to interpret the AU ROC score? ⭐️
AUC score is the value of Area Under the ROC Curve.
If we assume ROC curve consists of dots, , then
An excellent model has AUC near to the 1 which means it has good measure of separability. A poor model has AUC near to the 0 which means it has worst measure of separability. When AUC score is 0.5, it means model has no class separation capacity whatsoever.
What is the PR (precision-recall) curve? ⭐️
A precision-recall curve (or PR Curve) is a plot of the precision (y-axis) and the recall (x-axis) for different probability thresholds. Precision-recall curves (PR curves) are recommended for highly skewed domains where ROC curves may provide an excessively optimistic view of the performance.
What is the area under the PR curve? Is it a useful metric? ⭐️I
The Precision-Recall AUC is just like the ROC AUC, in that it summarizes the curve with a range of threshold values as a single score.
A high area under the curve represents both high recall and high precision, where high precision relates to a low false positive rate, and high recall relates to a low false negative rate.
In which cases AU PR is better than AU ROC? ⭐️
What is different however is that AU ROC looks at a true positive rate TPR and false positive rate FPR while AU PR looks at positive predictive value PPV and true positive rate TPR.
Typically, if true negatives are not meaningful to the problem or you care more about the positive class, AU PR is typically going to be more useful; otherwise, If you care equally about the positive and negative class or your dataset is quite balanced, then going with AU ROC is a good idea.
What do we do with categorical variables? ⭐️
Categorical variables must be encoded before they can be used as features to train a machine learning model. There are various encoding techniques, including:
- One-hot encoding
- Label encoding
- Ordinal encoding
- Target encoding
Why do we need one-hot encoding? ⭐️
If we simply encode categorical variables with a Label encoder, they become ordinal which can lead to undesirable consequences. In this case, linear models will treat category with id 4 as twice better than a category with id 2. One-hot encoding allows us to represent a categorical variable in a numerical vector space which ensures that vectors of each category have equal distances between each other. This approach is not suited for all situations, because by using it with categorical variables of high cardinality (e.g. customer id) we will encounter problems that come into play because of the curse of dimensionality.
What happens to our linear regression model if we have three columns in our data: x, y, z — and z is a sum of x and y? ⭐️
We would not be able to perform the resgression. Beacuse z is linearly dependent on x and y so when performing the regression would be a singular (not invertible) matrix.
What happens to our linear regression model if the column z in the data is a sum of columns x and y and some random noise? ⭐️
Answer here
What is regularization? Why do we need it? 👶
Regularization is used to reduce overfitting in machine learning models. It helps the models to generalize well and make them robust to outliers and noise in the data.
Which regularization techniques do you know? ⭐️
There are mainly two types of regularization,
- L1 Regularization (Lasso regularization) - Adds the sum of absolute values of the coefficients to the cost function.
- L2 Regularization (Ridge regularization) - Adds the sum of squares of coefficients to the cost function.
What kind of regularization techniques are applicable to linear models? ⭐️
AIC/BIC, Ridge regression, Lasso, Elastic Net, Basis pursuit denoising, Rudin–Osher–Fatemi model (TV), Potts model, RLAD, Dantzig Selector,SLOPE
How does L2 regularization look like in a linear model? ⭐️
L2 regularization adds a penalty term to our cost function which is equal to the sum of squares of models coefficients multiplied by a lambda hyperparameter. This technique makes sure that the coefficients are close to zero and is widely used in cases when we have a lot of features that might correlate with each other.
How do we select the right regularization parameters? 👶
Answer here
What’s the effect of L2 regularization on the weights of a linear model? ⭐️
L2 regularization penalizes larger weights more severely (due to the squared penalty term), which encourages weight values to decay toward zero.
How L1 regularization looks like in a linear model? ⭐️
Answer here
What’s the difference between L2 and L1 regularization? ⭐️
- Penalty terms: L1 regularization uses the sum of the absolute values of the weights, while L2 regularization uses the sum of the weights squared.
- Feature selection: L1 performs feature selection by reducing the coefficients of some predictors to 0, while L2 does not.
- Computational efficiency: L2 has an analytical solution, while L1 does not.
- Multicollinearity: L2 addresses multicollinearity by constraining the coefficient norm.
Can we have both L1 and L2 regularization components in a linear model? ⭐️
Yes, elastic net regularization combines L1 and L2 regularization.
What’s the interpretation of the bias term in linear models? ⭐️
Bias is simply, a difference between predicted value and actual/true value. It can be interpreted as the distance from the average prediction and true value i.e. true value minus mean(predictions). But dont get confused between accuracy and bias.
How do we interpret weights in linear models? ⭐️
Without normalizing weights or variables, if you increase the corresponding predictor by one unit, the coefficient represents on average how much the output changes. By the way, this interpretation still works for logistic regression - if you increase the corresponding predictor by one unit, the weight represents the change in the log of the odds.
If the variables are normalized, we can interpret weights in linear models like the importance of this variable in the predicted result.
If a weight for one variable is higher than for another — can we say that this variable is more important? ⭐️
Yes - if your predictor variables are normalized.
Without normalization, the weight represents the change in the output per unit change in the predictor. If you have a predictor with a huge range and scale that is used to predict an output with a very small range - for example, using each nation's GDP to predict maternal mortality rates - your coefficient should be very small. That does not necessarily mean that this predictor variable is not important compared to the others.
When do we need to perform feature normalization for linear models? When it’s okay not to do it? ⭐️
Answer here
What is feature selection? Why do we need it? 👶
Feature Selection is a method used to select the relevant features for the model to train on. We need feature selection to remove the irrelevant features which leads the model to under-perform.
Is feature selection important for linear models? ⭐️
Answer here
Which feature selection techniques do you know? ⭐️
Here are some of the feature selections:
- Principal Component Analysis
- Neighborhood Component Analysis
- ReliefF Algorithm
Can we use L1 regularization for feature selection? ⭐️
Yes, because the nature of L1 regularization will lead to sparse coefficients of features. Feature selection can be done by keeping only features with non-zero coefficients.
Can we use L2 regularization for feature selection? ⭐️
Answer here
What are the decision trees? 👶
This is a type of supervised learning algorithm that is mostly used for classification problems. Surprisingly, it works for both categorical and continuous dependent variables.
In this algorithm, we split the population into two or more homogeneous sets. This is done based on most significant attributes/ independent variables to make as distinct groups as possible.
A decision tree is a flowchart-like tree structure, where each internal node (non-leaf node) denotes a test on an attribute, each branch represents an outcome of the test, and each leaf node (or terminal node) holds a value for the target variable.
Various techniques : like Gini, Information Gain, Chi-square, entropy.
How do we train decision trees? ⭐️
- Start at the root node.
- For each variable X, find the set S_1 that minimizes the sum of the node impurities in the two child nodes and choose the split {X*,S*} that gives the minimum over all X and S.
- If a stopping criterion is reached, exit. Otherwise, apply step 2 to each child node in turn.
What are the main parameters of the decision tree model? 👶
- maximum tree depth
- minimum samples per leaf node
- impurity criterion
How do we handle categorical variables in decision trees? ⭐️
Some decision tree algorithms can handle categorical variables out of the box, others cannot. However, we can transform categorical variables, e.g. with a binary or a one-hot encoder.
What are the benefits of a single decision tree compared to more complex models? ⭐️
- easy to implement
- fast training
- fast inference
- good explainability
How can we know which features are more important for the decision tree model? ⭐️
Often, we want to find a split such that it minimizes the sum of the node impurities. The impurity criterion is a parameter of decision trees. Popular methods to measure the impurity are the Gini impurity and the entropy describing the information gain.
What is random forest? 👶
Random Forest is a machine learning method for regression and classification which is composed of many decision trees. Random Forest belongs to a larger class of ML algorithms called ensemble methods (in other words, it involves the combination of several models to solve a single prediction problem).
Why do we need randomization in random forest? ⭐️
Random forest in an extention of the bagging algorithm which takes random data samples from the training dataset (with replacement), trains several models and averages predictions. In addition to that, each time a split in a tree is considered, random forest takes a random sample of m features from full set of n features (with replacement) and uses this subset of features as candidates for the split (for example, m = sqrt(n)).
Training decision trees on random data samples from the training dataset reduces variance. Sampling features for each split in a decision tree decorrelates trees.
What are the main parameters of the random forest model? ⭐️
max_depth: Longest Path between root node and the leafmin_sample_split: The minimum number of observations needed to split a given nodemax_leaf_nodes: Conditions the splitting of the tree and hence, limits the growth of the treesmin_samples_leaf: minimum number of samples in the leaf noden_estimators: Number of treesmax_sample: Fraction of original dataset given to any individual tree in the given modelmax_features: Limits the maximum number of features provided to trees in random forest model
How do we select the depth of the trees in random forest? ⭐️
The greater the depth, the greater amount of information is extracted from the tree, however, there is a limit to this, and the algorithm even if defensive against overfitting may learn complex features of noise present in data and as a result, may overfit on noise. Hence, there is no hard thumb rule in deciding the depth, but literature suggests a few tips on tuning the depth of the tree to prevent overfitting:
- limit the maximum depth of a tree
- limit the number of test nodes
- limit the minimum number of objects at a node required to split
- do not split a node when, at least, one of the resulting subsample sizes is below a given threshold
- stop developing a node if it does not sufficiently improve the fit.
How do we know how many trees we need in random forest? ⭐️
The number of trees in random forest is worked by n_estimators, and a random forest reduces overfitting by increasing the number of trees. There is no fixed thumb rule to decide the number of trees in a random forest, it is rather fine tuned with the data, typically starting off by taking the square of the number of features (n) present in the data followed by tuning until we get the optimal results.
Is it easy to parallelize training of a random forest model? How can we do it? ⭐️
Yes, R provides a simple way to parallelize training of random forests on large scale data. It makes use of a parameter called multicombine which can be set to TRUE for parallelizing random forest computations.
rf <- foreach(ntree=rep(25000, 6), .combine=randomForest::combine,
.multicombine=TRUE, .packages='randomForest') %dopar% {
randomForest(x, y, ntree=ntree)
}What are the potential problems with many large trees? ⭐️
Answer here
What if instead of finding the best split, we randomly select a few splits and just select the best from them. Will it work? 🚀
Answer here
What happens when we have correlated features in our data? ⭐️
In random forest, since random forest samples some features to build each tree, the information contained in correlated features is twice as much likely to be picked than any other information contained in other features.
In general, when you are adding correlated features, it means that they linearly contains the same information and thus it will reduce the robustness of your model. Each time you train your model, your model might pick one feature or the other to "do the same job" i.e. explain some variance, reduce entropy, etc.
What is gradient boosting trees? ⭐️
Gradient boosting is a machine learning technique for regression and classification problems, which produces a prediction model in the form of an ensemble of weak prediction models, typically decision trees.
What’s the difference between random forest and gradient boosting? ⭐️
- Random Forests builds each tree independently while Gradient Boosting builds one tree at a time.
- Random Forests combine results at the end of the process (by averaging or "majority rules") while Gradient Boosting combines results along the way.
Is it possible to parallelize training of a gradient boosting model? How to do it? ⭐️
Answer here
Feature importance in gradient boosting trees — what are possible options? ⭐️
Answer here
Are there any differences between continuous and discrete variables when it comes to feature importance of gradient boosting models? 🚀
Answer here
What are the main parameters in the gradient boosting model? ⭐️
There are many parameters, but below are a few key defaults.
- learning_rate=0.1 (shrinkage).
- n_estimators=100 (number of trees).
- max_depth=3.
- min_samples_split=2.
- min_samples_leaf=1.
- subsample=1.0.
How do you approach tuning parameters in XGBoost or LightGBM? 🚀
Answer here
How do you select the number of trees in the gradient boosting model? ⭐️
Most implementations of gradient boosting are configured by default with a relatively small number of trees, such as hundreds or thousands. Using scikit-learn we can perform a grid search of the n_estimators model parameter
Which hyper-parameter tuning strategies (in general) do you know? ⭐️
There are several strategies for hyper-tuning but I would argue that the three most popular nowadays are the following:
-
Grid Search is an exhaustive approach such that for each hyper-parameter, the user needs to manually give a list of values for the algorithm to try. After these values are selected, grid search then evaluates the algorithm using each and every combination of hyper-parameters and returns the combination that gives the optimal result (i.e. lowest MAE). Because grid search evaluates the given algorithm using all combinations, it's easy to see that this can be quite computationally expensive and can lead to sub-optimal results specifically since the user needs to specify specific values for these hyper-parameters, which is prone for error and requires domain knowledge.
-
Random Search is similar to grid search but differs in the sense that rather than specifying which values to try for each hyper-parameter, an upper and lower bound of values for each hyper-parameter is given instead. With uniform probability, random values within these bounds are then chosen and similarly, the best combination is returned to the user. Although this seems less intuitive, no domain knowledge is necessary and theoretically much more of the parameter space can be explored.
-
In a completely different framework, Bayesian Optimization is thought of as a more statistical way of optimization and is commonly used when using neural networks, specifically since one evaluation of a neural network can be computationally costly. In numerous research papers, this method heavily outperforms Grid Search and Random Search and is currently used on the Google Cloud Platform as well as AWS. Because an in-depth explanation requires a heavy background in bayesian statistics and gaussian processes (and maybe even some game theory), a "simple" explanation is that a much simpler/faster acquisition function intelligently chooses (using a surrogate function such as probability of improvement or GP-UCB) which hyper-parameter values to try on the computationally expensive, original algorithm. Using the result of the initial combination of values on the expensive/original function, the acquisition function takes the result of the expensive/original algorithm into account and uses it as its prior knowledge to again come up with another set of hyper-parameters to choose during the next iteration. This process continues either for a specified number of iterations or for a specified amount of time and similarly the combination of hyper-parameters that performs the best on the expensive/original algorithm is chosen.
What’s the difference between grid search parameter tuning strategy and random search? When to use one or another? ⭐️
For specifics, refer to the above answer.
What kind of problems neural nets can solve? 👶
Neural nets are good at solving non-linear problems. Some good examples are problems that are relatively easy for humans (because of experience, intuition, understanding, etc), but difficult for traditional regression models: speech recognition, handwriting recognition, image identification, etc.
How does a usual fully-connected feed-forward neural network work? ⭐️
Answer here
Why do we need activation functions? 👶
The main idea of using neural networks is to learn complex nonlinear functions. If we are not using an activation function in between different layers of a neural network, we are just stacking up multiple linear layers one on top of another and this leads to learning a linear function. The Nonlinearity comes only with the activation function, this is the reason we need activation functions.
What are the problems with sigmoid as an activation function? ⭐️
The derivative of the sigmoid function for large positive or negative numbers is almost zero. From this comes the problem of vanishing gradient — during the backpropagation our net will not learn (or will learn drastically slow). One possible way to solve this problem is to use ReLU activation function.
What is ReLU? How is it better than sigmoid or tanh? ⭐️
ReLU is an abbreviation for Rectified Linear Unit. It is an activation function which has the value 0 for all negative values and the value f(x) = x for all positive values. The ReLU has a simple activation function which makes it fast to compute and while the sigmoid and tanh activation functions saturate at higher values, the ReLU has a potentially infinite activation, which addresses the problem of vanishing gradients.
How we can initialize the weights of a neural network? ⭐️
Proper initialization of weight matrix in neural network is very necessary. Simply we can say there are two ways for initializtions.
- Initializing weights with zeroes. Setting weights to zero makes your network no better than a linear model. It is important to note that setting biases to 0 will not create any troubles as non zero weights take care of breaking the symmetry and even if bias is 0, the values in every neuron are still different.
- Initializing weights randomly. Assigning random values to weights is better than just 0 assignment.
- a) If weights are initialized with very high values the term np.dot(W,X)+b becomes significantly higher and if an activation function like sigmoid() is applied, the function maps its value near to 1 where the slope of gradient changes slowly and learning takes a lot of time.
- b) If weights are initialized with low values it gets mapped to 0, where the case is the same as above. This problem is often referred to as the vanishing gradient.
What if we set all the weights of a neural network to 0? ⭐️
If all the weights of a neural network are set to zero, the output of each connection is same (W*x = 0). This means the gradients which are backpropagated to each connection in a layer is same. This means all the connections/weights learn the same thing, and the model never converges.
What regularization techniques for neural nets do you know? ⭐️
- L1 Regularization - Defined as the sum of absolute values of the individual parameters. The L1 penalty causes a subset of the weights to become zero, suggesting that the corresponding features may safely be discarded.
- L2 Regularization - Defined as the sum of square of individual parameters. Often supported by regularization hyperparameter alpha. It results in weight decay.
- Data Augmentation - This requires some fake data to be created as a part of training set.
- Drop Out : This is most effective regularization technique for newral nets. Few randome nodes in each layer is deactivated in forward pass. This allows the algorithm to train on different set of nodes in each iterations.
What is dropout? Why is it useful? How does it work? ⭐️
Dropout is a technique that at each training step turns off each neuron with a certain probability of p. This way at each iteration we train only 1-p of neurons, which forces the network not to rely only on the subset of neurons for feature representation. This leads to regularizing effects that are controlled by the hyperparameter p.
What is backpropagation? How does it work? Why do we need it? ⭐️
The Backpropagation algorithm looks for the minimum value of the error function in weight space using a technique called the delta rule or gradient descent. The weights that minimize the error function is then considered to be a solution to the learning problem.
We need backpropogation because,
- Calculate the error – How far is your model output from the actual output.
- Minimum Error – Check whether the error is minimized or not.
- Update the parameters – If the error is huge then, update the parameters (weights and biases). After that again check the error.
Repeat the process until the error becomes minimum. - Model is ready to make a prediction – Once the error becomes minimum, you can feed some inputs to your model and it will produce the output.
Which optimization techniques for training neural nets do you know? ⭐️
- Gradient Descent
- Stochastic Gradient Descent
- Mini-Batch Gradient Descent(best among gradient descents)
- Nesterov Accelerated Gradient
- Momentum
- Adagrad
- AdaDelta
- Adam(best one. less time, more efficient)
How do we use SGD (stochastic gradient descent) for training a neural net? ⭐️
Answer here
What’s the learning rate? 👶
The learning rate is an important hyperparameter that controls how quickly the model is adapted to the problem during the training. It can be seen as the "step width" during the parameter updates, i.e. how far the weights are moved into the direction of the minimum of our optimization problem.
What happens when the learning rate is too large? Too small? 👶
A large learning rate can accelerate the training. However, it is possible that we "shoot" too far and miss the minimum of the function that we want to optimize, which will not result in the best solution. On the other hand, training with a small learning rate takes more time but it is possible to find a more precise minimum. The downside can be that the solution is stuck in a local minimum, and the weights won't update even if it is not the best possible global solution.
How to set the learning rate? ⭐️
Answer here
What is Adam? What’s the main difference between Adam and SGD? ⭐️
Adam (Adaptive Moment Estimation) is a optimization technique for training neural networks. on an average, it is the best optimizer .It works with momentums of first and second order. The intuition behind the Adam is that we don’t want to roll so fast just because we can jump over the minimum, we want to decrease the velocity a little bit for a careful search.
Adam tends to converge faster, while SGD often converges to more optimal solutions. SGD's high variance disadvantages gets rectified by Adam (as advantage for Adam).
When would you use Adam and when SGD? ⭐️
Adam tends to converge faster, while SGD often converges to more optimal solutions.
Do we want to have a constant learning rate or we better change it throughout training? ⭐️
Answer here
How do we decide when to stop training a neural net? 👶
Simply stop training when the validation error is the minimum.
What is model checkpointing? ⭐️
Answer here
Can you tell us how you approach the model training process? ⭐️
Answer here
How we can use neural nets for computer vision? ⭐️
Answer here
What’s a convolutional layer? ⭐️
The idea of the convolutional layer is the assumption that the information needed for making a decision often is spatially close and thus, it only takes the weighted sum over nearby inputs. It also assumes that the networks’ kernels can be reused for all nodes, hence the number of weights can be drastically reduced. To counteract only one feature being learnt per layer, multiple kernels are applied to the input which creates parallel channels in the output. Consecutive layers can also be stacked to allow the network to find more high-level features.
Why do we actually need convolutions? Can’t we use fully-connected layers for that? ⭐️
A fully-connected layer needs one weight per inter-layer connection, which means the number of weights which needs to be computed quickly balloons as the number of layers and nodes per layer is increased.
What’s pooling in CNN? Why do we need it? ⭐️
Pooling is a technique to downsample the feature map. It allows layers which receive relatively undistorted versions of the input to learn low level features such as lines, while layers deeper in the model can learn more abstract features such as texture.
How does max pooling work? Are there other pooling techniques? ⭐️
Max pooling is a technique where the maximum value of a receptive field is passed on in the next feature map. The most commonly used receptive field is 2 x 2 with a stride of 2, which means the feature map is downsampled from N x N to N/2 x N/2. Receptive fields larger than 3 x 3 are rarely employed as too much information is lost.
Other pooling techniques include:
- Average pooling, the output is the average value of the receptive field.
- Min pooling, the output is the minimum value of the receptive field.
- Global pooling, where the receptive field is set to be equal to the input size, this means the output is equal to a scalar and can be used to reduce the dimensionality of the feature map.
Are CNNs resistant to rotations? What happens to the predictions of a CNN if an image is rotated? 🚀
Answer here
What are augmentations? Why do we need them? 👶
Answer here
What kind of augmentations do you know? 👶
Answer here
How to choose which augmentations to use? ⭐️
Answer here
What kind of CNN architectures for classification do you know? 🚀
Answer here
What is transfer learning? How does it work? ⭐️
Given a source domain D_S and learning task T_S, a target domain D_T and learning task T_T, transfer learning aims to help improve the learning of the target predictive function f_T in D_T using the knowledge in D_S and T_S, where D_S ≠ D_T,or T_S ≠ T_T. In other words, transfer learning enables to reuse knowledge coming from other domains or learning tasks.
In the context of CNNs, we can use networks that were pre-trained on popular datasets such as ImageNet. We then can use the weights of the layers that learn to represent features and combine them with a new set of layers that learns to map the feature representations to the given classes. Two popular strategies are either to freeze the layers that learn the feature representations completely, or to give them a smaller learning rate.
What is object detection? Do you know any architectures for that? 🚀
Answer here
What is object segmentation? Do you know any architectures for that? 🚀
Answer here
How can we use machine learning for text classification? ⭐️
Answer here
What is bag of words? How we can use it for text classification? ⭐️
Bag of Words is a representation of text that describes the occurrence of words within a document. The order or structure of the words is not considered. For text classification, we look at the histogram of the words within the text and consider each word count as a feature.
What are the advantages and disadvantages of bag of words? ⭐️
Advantages:
- Simple to understand and implement.
Disadvantages:
- The vocabulary requires careful design, most specifically in order to manage the size, which impacts the sparsity of the document representations.
- Sparse representations are harder to model both for computational reasons (space and time complexity) and also for information reasons
- Discarding word order ignores the context, and in turn meaning of words in the document. Context and meaning can offer a lot to the model, that if modeled could tell the difference between the same words differently arranged (“this is interesting” vs “is this interesting”), synonyms (“old bike” vs “used bike”).
What are N-grams? How can we use them? ⭐️
The function to tokenize into consecutive sequences of words is called n-grams. It can be used to find out N most co-occurring words (how often word X is followed by word Y) in a given sentence.
How large should be N for our bag of words when using N-grams? ⭐️
Answer here
What is TF-IDF? How is it useful for text classification? ⭐️
Term Frequency (TF) is a scoring of the frequency of the word in the current document. Inverse Document Frequency(IDF) is a scoring of how rare the word is across documents. It is used in scenario where highly recurring words may not contain as much informational content as the domain specific words. For example, words like “the” that are frequent across all documents therefore need to be less weighted. The TF-IDF score highlights words that are distinct (contain useful information) in a given document.
Which model would you use for text classification with bag of words features? ⭐️
Answer here
Would you prefer gradient boosting trees model or logistic regression when doing text classification with bag of words? ⭐️
Usually logistic regression is better because bag of words creates a matrix with large number of columns. For a huge number of columns logistic regression is usually faster than gradient boosting trees.
What are word embeddings? Why are they useful? Do you know Word2Vec? ⭐️
Answer here
Do you know any other ways to get word embeddings? 🚀
Answer here
If you have a sentence with multiple words, you may need to combine multiple word embeddings into one. How would you do it? ⭐️
Approaches ranked from simple to more complex:
- Take an average over all words
- Take a weighted average over all words. Weighting can be done by inverse document frequency (idf part of tf-idf).
- Use ML model like LSTM or Transformer.
Would you prefer gradient boosting trees model or logistic regression when doing text classification with embeddings? ⭐️
Answer here
How can you use neural nets for text classification? 🚀
Answer here
How can we use CNN for text classification? 🚀
Answer here
What is unsupervised learning? 👶
Unsupervised learning aims to detect paterns in data where no labels are given.
What is clustering? When do we need it? 👶
Clustering algorithms group objects such that similar feature points are put into the same groups (clusters) and dissimilar feature points are put into different clusters.
Do you know how K-means works? ⭐️
- Partition points into k subsets.
- Compute the seed points as the new centroids of the clusters of the current partitioning.
- Assign each point to the cluster with the nearest seed point.
- Go back to step 2 or stop when the assignment does not change.
How to select K for K-means? ⭐️
- Domain knowledge, i.e. an expert knows the value of k
- Elbow method: compute the clusters for different values of k, for each k, calculate the total within-cluster sum of square, plot the sum according to the number of clusters and use the band as the number of clusters.
- Average silhouette method: compute the clusters for different values of k, for each k, calculate the average silhouette of observations, plot the silhouette according to the number of clusters and select the maximum as the number of clusters.
What are the other clustering algorithms do you know? ⭐️
- k-medoids: Takes the most central point instead of the mean value as the center of the cluster. This makes it more robust to noise.
- Agglomerative Hierarchical Clustering (AHC): hierarchical clusters combining the nearest clusters starting with each point as its own cluster.
- DIvisive ANAlysis Clustering (DIANA): hierarchical clustering starting with one cluster containing all points and splitting the clusters until each point describes its own cluster.
- Density-Based Spatial Clustering of Applications with Noise (DBSCAN): Cluster defined as maximum set of density-connected points.
Do you know how DBScan works? ⭐️
- Two input parameters epsilon (neighborhood radius) and minPts (minimum number of points in an epsilon-neighborhood)
- Cluster defined as maximum set of density-connected points.
- Points p_j and p_i are density-connected w.r.t. epsilon and minPts if there is a point o such that both, i and j are density-reachable from o w.r.t. epsilon and minPts.
- p_j is density-reachable from p_i w.r.t. epsilon, minPts if there is a chain of points p_i -> p_i+1 -> p_i+x = p_j such that p_i+x is directly density-reachable from p_i+x-1.
- p_j is a directly density-reachable point of the neighborhood of p_i if dist(p_i,p_j) <= epsilon.
When would you choose K-means and when DBScan? ⭐️
- DBScan is more robust to noise.
- DBScan is better when the amount of clusters is difficult to guess.
- K-means has a lower complexity, i.e. it will be much faster, especially with a larger amount of points.
What is the curse of dimensionality? Why do we care about it? ⭐️
Data in only one dimension is relatively tightly packed. Adding a dimension stretches the points across that dimension, pushing them further apart. Additional dimensions spread the data even further making high dimensional data extremely sparse. We care about it, because it is difficult to use machine learning in sparse spaces.
Do you know any dimensionality reduction techniques? ⭐️
- Singular Value Decomposition (SVD)
- Principal Component Analysis (PCA)
- Linear Discriminant Analysis (LDA)
- T-distributed Stochastic Neighbor Embedding (t-SNE)
- Autoencoders
- Fourier and Wavelet Transforms
What’s singular value decomposition? How is it typically used for machine learning? ⭐️
- Singular Value Decomposition (SVD) is a general matrix decomposition method that factors a matrix X into three matrices L (left singular values), Σ (diagonal matrix) and R^T (right singular values).
- For machine learning, Principal Component Analysis (PCA) is typically used. It is a special type of SVD where the singular values correspond to the eigenvectors and the values of the diagonal matrix are the squares of the eigenvalues. We use these features as they are statistically descriptive.
- Having calculated the eigenvectors and eigenvalues, we can use the Kaiser-Guttman criterion, a scree plot or the proportion of explained variance to determine the principal components (i.e. the final dimensionality) that are useful for dimensionality reduction.
What is the ranking problem? Which models can you use to solve them? ⭐️
Answer here
What are good unsupervised baselines for text information retrieval? ⭐️
Answer here
How would you evaluate your ranking algorithms? Which offline metrics would you use? ⭐️
Answer here
What is precision and recall at k? ⭐️
Precision at k and recall at k are evaluation metrics for ranking algorithms. Precision at k shows the share of relevant items in the first k results of the ranking algorithm. And Recall at k indicates the share of relevant items returned in top k results out of all correct answers for a given query.
Example: For a search query "Car" there are 3 relevant products in your shop. Your search algorithm returns 2 of those relevant products in the first 5 search results. Precision at 5 = # num of relevant products in search result / k = 2/5 = 40% Recall at 5 = # num of relevant products in search result / # num of all relevant products = 2/3 = 66.6%
What is mean average precision at k? ⭐️
Answer here
How can we use machine learning for search? ⭐️
Answer here
How can we get training data for our ranking algorithms? ⭐️
Answer here
Can we formulate the search problem as a classification problem? How? ⭐️
Answer here
How can we use clicks data as the training data for ranking algorithms? 🚀
Answer here
Do you know how to use gradient boosting trees for ranking? 🚀
Answer here
How do you do an online evaluation of a new ranking algorithm? ⭐️
Answer here
What is a recommender system? 👶
Recommender systems are software tools and techniques that provide suggestions for items that are most likely of interest to a particular user.
What are good baselines when building a recommender system? ⭐️
- A good recommer system should give relevant and personalized information.
- It should not recommend items the user knows well or finds easily.
- It should make diverse suggestions.
- A user should explore new items.
What is collaborative filtering? ⭐️
- Collaborative filtering is the most prominent approach to generate recommendations.
- It uses the wisdom of the crowd, i.e. it gives recommendations based on the experience of others.
- A recommendation is calculated as the average of other experiences.
- Say we want to give a score that indicates how much user u will like an item i. Then we can calculate it with the experience of N other users U as r_ui = 1/N * sum(v in U) r_vi.
- In order to rate similar experiences with a higher weight, we can introduce a similarity between users that we use as a multiplier for each rating.
- Also, as users have an individual profile, one user may have an average rating much larger than another user, so we use normalization techniques (e.g. centering or Z-score normalization) to remove the users' biases.
- Collaborative filtering does only need a rating matrix as input and improves over time. However, it does not work well on sparse data, does not work for cold starts (see below) and usually tends to overfit.
How we can incorporate implicit feedback (clicks, etc) into our recommender systems? ⭐️
In comparison to explicit feedback, implicit feedback datasets lack negative examples. For example, explicit feedback can be a positive or a negative rating, but implicit feedback may be the number of purchases or clicks. One popular approach to solve this problem is named weighted alternating least squares (wALS) [Hu, Y., Koren, Y., & Volinsky, C. (2008, December). Collaborative filtering for implicit feedback datasets. In Data Mining, 2008. ICDM'08. Eighth IEEE International Conference on (pp. 263-272). IEEE.]. Instead of modeling the rating matrix directly, the numbers (e.g. amount of clicks) describe the strength in observations of user actions. The model tries to find latent factors that can be used to predict the expected preference of a user for an item.
What is the cold start problem? ⭐️
Collaborative filterung incorporates crowd knowledge to give recommendations for certain items. Say we want to recommend how much a user will like an item, we then will calculate the score using the recommendations of other users for this certain item. We can distinguish between two different ways of a cold start problem now. First, if there is a new item that has not been rated yet, we cannot give any recommendation. Also, when there is a new user, we cannot calculate a similarity to any other user.
Possible approaches to solving the cold start problem? ⭐️🚀
- Content-based filtering incorporates features about items to calculate a similarity between them. In this way, we can recommend items that have a high similarity to items that a user liked already. In this way, we are not dependant on the ratings of other users for a given item anymore and solve the cold start problem for new items.
- Demographic filtering incorporates user profiles to calculate a similarity between them and solves the cold start problem for new users.
What is a time series? 👶
A time series is a set of observations ordered in time usually collected at regular intervals.
How is time series different from the usual regression problem? 👶
The principle behind causal forecasting is that the value that has to be predicted is dependant on the input features (causal factors). In time series forecasting, the to be predicted value is expected to follow a certain pattern over time.
Which models do you know for solving time series problems? ⭐️
- Simple Exponential Smoothing: approximate the time series with an exponentional function
- Trend-Corrected Exponential Smoothing (Holt‘s Method): exponential smoothing that also models the trend
- Trend- and Seasonality-Corrected Exponential Smoothing (Holt-Winter‘s Method): exponential smoothing that also models trend and seasonality
- Time Series Decomposition: decomposed a time series into the four components trend, seasonal variation, cycling varation and irregular component
- Autoregressive models: similar to multiple linear regression, except that the dependent variable y_t depends on its own previous values rather than other independent variables.
- Deep learning approaches (RNN, LSTM, etc.)
If there’s a trend in our series, how we can remove it? And why would we want to do it? ⭐️
We can explicitly model the trend (and/or seasonality) with approaches such as Holt's Method or Holt-Winter's Method. We want to explicitly model the trend to reach the stationarity property for the data. Many time series approaches require stationarity. Without stationarity,the interpretation of the results of these analyses is problematic [Manuca, Radu & Savit, Robert. (1996). Stationarity and nonstationarity in time series analysis. Physica D: Nonlinear Phenomena. 99. 134-161. 10.1016/S0167-2789(96)00139-X. ].
You have a series with only one variable “y” measured at time t. How do predict “y” at time t+1? Which approaches would you use? ⭐️
We want to look at the correlation between different observations of y. This measure of correlation is called autocorrelation. Autoregressive models are multiple regression models where the time-lag series of the original time series are treated like multiple independent variables.
You have a series with a variable “y” and a set of features. How do you predict “y” at t+1? Which approaches would you use? ⭐️
Given the assumption that the set of features gives a meaningful causation to y, a causal forecasting approach such as linear regression or multiple nonlinear regression might be useful. In case there is a lot of data and the explanability of the results is not a high priority, we can also consider deep learning approaches.
What are the problems with using trees for solving time series problems? ⭐️
Random Forest models are not able to extrapolate time series data and understand increasing/decreasing trends. It will provide us with average data points if the validation data has values greater than the training data points.