A golang implementation of a sparse Merkle tree with efficient caching strategies. Note that this is a proof-of-concept implementation, please do not use for anything serious.
A sparse Merkle tree (SMT) is a Merkle (hash) tree that contains a leaf for every possible output of a hash function [0]. In other words, an SMT has 2^N leafs for a hash function with a N-bit output, so for example when using SHA-256 this means 2^256 leafs. Since the full in-memory representation of an SMT is impractical (to say the least) we have to simulate it, and it turns out that simulation is practical. This is because the tree is sparse: most leafs are empty, so when we calculate the hash of the empty leafs we get the same hash. The same is true for interior nodes whose children are all empty, and so on.
While the concept of an SMT is neat on its own, it gets better. When simulating an SMT we can keep a cache of previously calculated nodes in the SMT. The most obvious part is for all sparse nodes. Beyond that, there are a number of caching strategies that give different space-time trade-offs. One cool strategy is to make the cache probabilistic and smaller than the data to authenticate: let's say you have a database of n items, it turns out that only keeping a cache of size 0.6*n is practical for many applications.
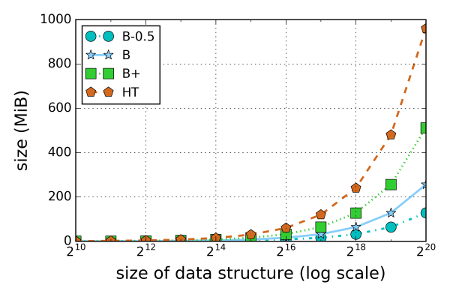
Below is a graph of the size of the authenticated data structure as a function of the size of the underlying data structure (the database to authenticate). We include a hash treap (HT) in our comparison: a good representation of related authenticated data structures that are explicity stored in memory [1]. For an SMT we show three caching stragies: B, B+, and B-0.5. The B cache stores all (non-default) branches in the tree, B+ all children of all branches in the tree, and B-0.5 stores 50% of all branches in the tree. As we can see, the size of the HT is roughly eight times larger than that of the B-0.5 cache.
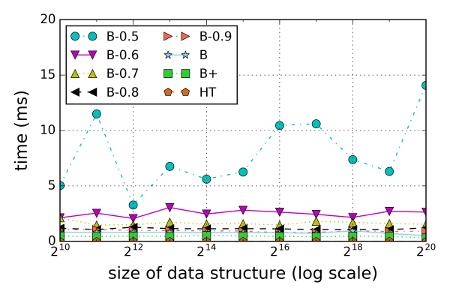
There is no such thing as a free lunch though. Below is the average time it takes to generate an (Merkle) audit path. We include a number of B- caches with different caching probabilities (note that the B cache is identical to B-1.0). While B-0.5 behaves erratic, B-0.6 and above needs less then 4ms. For many applications this is practical and saves a significant amount of space compared to explicity stored authenticated data structures.
You can reproduce these benchmarks with the cmd/benchht and cmd/benchsmt executables.
https://eprint.iacr.org/2016/683
Apache 2.0