Skip to content

Latest commit

 

History

History
538 lines (403 loc) · 18.3 KB

0108.将有序数组转换为二叉搜索树.md

File metadata and controls

538 lines (403 loc) · 18.3 KB
Raw

参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！

构造二叉搜索树，一不小心就平衡了

108.将有序数组转换为二叉搜索树

力扣题目链接

将一个按照升序排列的有序数组，转换为一棵高度平衡二叉搜索树。

本题中，一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。

示例:

108.将有序数组转换为二叉搜索树

算法公开课

《代码随想录》算法视频公开课：构造平衡二叉搜索树！| LeetCode：108.将有序数组转换为二叉搜索树，相信结合视频在看本篇题解，更有助于大家对本题的理解。

思路

做这道题目之前大家可以了解一下这几道：

进入正题：

题目中说要转换为一棵高度平衡二叉搜索树。为什么强调要平衡呢？

因为只要给我们一个有序数组，如果强调平衡，都可以以线性结构来构造二叉搜索树。

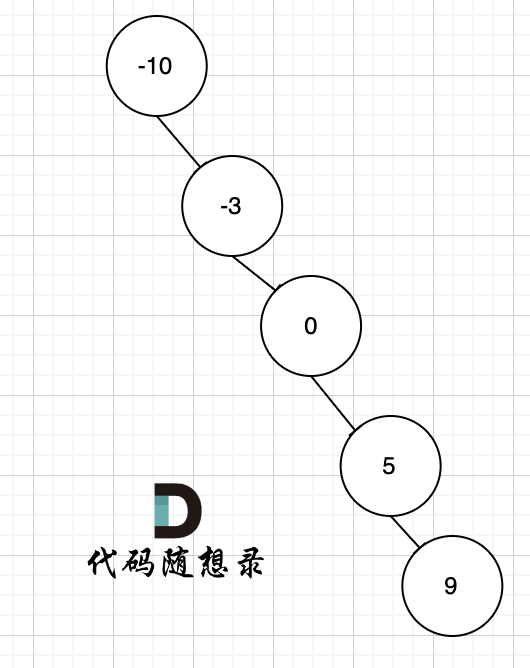
例如 有序数组[-10，-3，0，5，9] 就可以构造成这样的二叉搜索树，如图。

上图中，是符合二叉搜索树的特性吧，如果要这么做的话，是不是本题意义就不大了，所以才强调是平衡二叉搜索树。

其实数组构造二叉树，构成平衡树是自然而然的事情，因为大家默认都是从数组中间位置取值作为节点元素，一般不会随机取。所以想构成不平衡的二叉树是自找麻烦。

在二叉树：构造二叉树登场！和二叉树：构造一棵最大的二叉树中其实已经讲过了，如果根据数组构造一棵二叉树。

本质就是寻找分割点，分割点作为当前节点，然后递归左区间和右区间。

本题其实要比二叉树：构造二叉树登场！ 和 二叉树：构造一棵最大的二叉树简单一些，因为有序数组构造二叉搜索树，寻找分割点就比较容易了。

分割点就是数组中间位置的节点。

那么为问题来了，如果数组长度为偶数，中间节点有两个，取哪一个？

取哪一个都可以，只不过构成了不同的平衡二叉搜索树。

例如：输入：[-10,-3,0,5,9]

如下两棵树，都是这个数组的平衡二叉搜索树：

108.将有序数组转换为二叉搜索树

如果要分割的数组长度为偶数的时候，中间元素为两个，是取左边元素 就是树1，取右边元素就是树2。

这也是题目中强调答案不是唯一的原因。 理解这一点，这道题目算是理解到位了。

递归

递归三部曲：

  • 确定递归函数返回值及其参数

删除二叉树节点，增加二叉树节点，都是用递归函数的返回值来完成，这样是比较方便的。

相信大家如果仔细看了二叉树：搜索树中的插入操作和二叉树：搜索树中的删除操作，一定会对递归函数返回值的作用深有感触。

那么本题要构造二叉树，依然用递归函数的返回值来构造中节点的左右孩子。

再来看参数，首先是传入数组，然后就是左下标left和右下标right，我们在二叉树：构造二叉树登场！中提过，在构造二叉树的时候尽量不要重新定义左右区间数组，而是用下标来操作原数组。

所以代码如下：

// 左闭右闭区间[left, right]
TreeNode* traversal(vector<int>& nums, int left, int right)

这里注意，我这里定义的是左闭右闭区间，在不断分割的过程中，也会坚持左闭右闭的区间，这又涉及到我们讲过的循环不变量。

在二叉树：构造二叉树登场！，35.搜索插入位置 和59.螺旋矩阵II都详细讲过循环不变量。

  • 确定递归终止条件

这里定义的是左闭右闭的区间，所以当区间 left > right的时候，就是空节点了。

代码如下：

if (left > right) return nullptr;
  • 确定单层递归的逻辑

首先取数组中间元素的位置，不难写出int mid = (left + right) / 2;，这么写其实有一个问题，就是数值越界，例如left和right都是最大int，这么操作就越界了，在二分法中尤其需要注意！

所以可以这么写：int mid = left + ((right - left) / 2);

但本题leetcode的测试数据并不会越界，所以怎么写都可以。但需要有这个意识！

取了中间位置，就开始以中间位置的元素构造节点，代码：TreeNode* root = new TreeNode(nums[mid]);。

接着划分区间，root的左孩子接住下一层左区间的构造节点，右孩子接住下一层右区间构造的节点。

最后返回root节点，单层递归整体代码如下：

int mid = left + ((right - left) / 2);
TreeNode* root = new TreeNode(nums[mid]);
root->left = traversal(nums, left, mid - 1);
root->right = traversal(nums, mid + 1, right);
return root;

这里int mid = left + ((right - left) / 2);的写法相当于是如果数组长度为偶数，中间位置有两个元素，取靠左边的。

  • 递归整体代码如下：
class Solution {
private:
    TreeNode* traversal(vector<int>& nums, int left, int right) {
        if (left > right) return nullptr;
        int mid = left + ((right - left) / 2);
        TreeNode* root = new TreeNode(nums[mid]);
        root->left = traversal(nums, left, mid - 1);
        root->right = traversal(nums, mid + 1, right);
        return root;
    }
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        TreeNode* root = traversal(nums, 0, nums.size() - 1);
        return root;
    }
};

注意：在调用traversal的时候传入的left和right为什么是0和nums.size() - 1，因为定义的区间为左闭右闭。

迭代法

迭代法可以通过三个队列来模拟，一个队列放遍历的节点，一个队列放左区间下标，一个队列放右区间下标。

模拟的就是不断分割的过程，C++代码如下：（我已经详细注释）

class Solution {
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        if (nums.size() == 0) return nullptr;

        TreeNode* root = new TreeNode(0);   // 初始根节点
        queue<TreeNode*> nodeQue;           // 放遍历的节点
        queue<int> leftQue;                 // 保存左区间下标
        queue<int> rightQue;                // 保存右区间下标
        nodeQue.push(root);                 // 根节点入队列
        leftQue.push(0);                    // 0为左区间下标初始位置
        rightQue.push(nums.size() - 1);     // nums.size() - 1为右区间下标初始位置

        while (!nodeQue.empty()) {
            TreeNode* curNode = nodeQue.front();
            nodeQue.pop();
            int left = leftQue.front(); leftQue.pop();
            int right = rightQue.front(); rightQue.pop();
            int mid = left + ((right - left) / 2);

            curNode->val = nums[mid];       // 将mid对应的元素给中间节点

            if (left <= mid - 1) {          // 处理左区间
                curNode->left = new TreeNode(0);
                nodeQue.push(curNode->left);
                leftQue.push(left);
                rightQue.push(mid - 1);
            }

            if (right >= mid + 1) {         // 处理右区间
                curNode->right = new TreeNode(0);
                nodeQue.push(curNode->right);
                leftQue.push(mid + 1);
                rightQue.push(right);
            }
        }
        return root;
    }
};

总结

在二叉树：构造二叉树登场！ 和 二叉树：构造一棵最大的二叉树之后，我们顺理成章的应该构造一下二叉搜索树了，一不小心还是一棵平衡二叉搜索树。

其实思路也是一样的，不断中间分割，然后递归处理左区间，右区间，也可以说是分治。

此时相信大家应该对通过递归函数的返回值来增删二叉树很熟悉了，这也是常规操作。

在定义区间的过程中我们又一次强调了循环不变量的重要性。

最后依然给出迭代的方法，其实就是模拟取中间元素，然后不断分割去构造二叉树的过程。

其他语言版本

Java

递归: 左闭右开 [left,right)

class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        return sortedArrayToBST(nums, 0, nums.length);
    }
    
    public TreeNode sortedArrayToBST(int[] nums, int left, int right) {
        if (left >= right) {
            return null;
        }
        if (right - left == 1) {
            return new TreeNode(nums[left]);
        }
        int mid = left + (right - left) / 2;
        TreeNode root = new TreeNode(nums[mid]);
        root.left = sortedArrayToBST(nums, left, mid);
        root.right = sortedArrayToBST(nums, mid + 1, right);
        return root;
    }
}

递归: 左闭右闭 [left,right]

class Solution {
	public TreeNode sortedArrayToBST(int[] nums) {
		TreeNode root = traversal(nums, 0, nums.length - 1);
		return root;
	}

	// 左闭右闭区间[left, right]
	private TreeNode traversal(int[] nums, int left, int right) {
		if (left > right) return null;

		int mid = left + ((right - left) >> 1);
		TreeNode root = new TreeNode(nums[mid]);
		root.left = traversal(nums, left, mid - 1);
		root.right = traversal(nums, mid + 1, right);
		return root;
	}
}

迭代: 左闭右闭 [left,right]

class Solution {
	public TreeNode sortedArrayToBST(int[] nums) {
		if (nums.length == 0) return null;

		//根节点初始化
		TreeNode root = new TreeNode(-1);
		Queue<TreeNode> nodeQueue = new LinkedList<>();
		Queue<Integer> leftQueue = new LinkedList<>();
		Queue<Integer> rightQueue = new LinkedList<>();

		// 根节点入队列
		nodeQueue.offer(root);
		// 0为左区间下标初始位置
		leftQueue.offer(0);
		// nums.size() - 1为右区间下标初始位置
		rightQueue.offer(nums.length - 1);

		while (!nodeQueue.isEmpty()) {
			TreeNode currNode = nodeQueue.poll();
			int left = leftQueue.poll();
			int right = rightQueue.poll();
			int mid = left + ((right - left) >> 1);

			// 将mid对应的元素给中间节点
			currNode.val = nums[mid];

			// 处理左区间
			if (left <= mid - 1) {
				currNode.left = new TreeNode(-1);
				nodeQueue.offer(currNode.left);
				leftQueue.offer(left);
				rightQueue.offer(mid - 1);
			}

			// 处理右区间
			if (right >= mid + 1) {
				currNode.right = new TreeNode(-1);
				nodeQueue.offer(currNode.right);
				leftQueue.offer(mid + 1);
				rightQueue.offer(right);
			}
		}
		return root;
	}
}

Python

递归法

class Solution:
    def traversal(self, nums: List[int], left: int, right: int) -> TreeNode:
        if left > right:
            return None
        
        mid = left + (right - left) // 2
        root = TreeNode(nums[mid])
        root.left = self.traversal(nums, left, mid - 1)
        root.right = self.traversal(nums, mid + 1, right)
        return root
    
    def sortedArrayToBST(self, nums: List[int]) -> TreeNode:
        root = self.traversal(nums, 0, len(nums) - 1)
        return root

迭代法

from collections import deque

class Solution:
    def sortedArrayToBST(self, nums: List[int]) -> TreeNode:
        if len(nums) == 0:
            return None
        
        root = TreeNode(0)  # 初始根节点
        nodeQue = deque()   # 放遍历的节点
        leftQue = deque()   # 保存左区间下标
        rightQue = deque()  # 保存右区间下标
        
        nodeQue.append(root)               # 根节点入队列
        leftQue.append(0)                  # 0为左区间下标初始位置
        rightQue.append(len(nums) - 1)     # len(nums) - 1为右区间下标初始位置

        while nodeQue:
            curNode = nodeQue.popleft()
            left = leftQue.popleft()
            right = rightQue.popleft()
            mid = left + (right - left) // 2

            curNode.val = nums[mid]  # 将mid对应的元素给中间节点

            if left <= mid - 1:  # 处理左区间
                curNode.left = TreeNode(0)
                nodeQue.append(curNode.left)
                leftQue.append(left)
                rightQue.append(mid - 1)

            if right >= mid + 1:  # 处理右区间
                curNode.right = TreeNode(0)
                nodeQue.append(curNode.right)
                leftQue.append(mid + 1)
                rightQue.append(right)

        return root

Go

递归（隐含回溯）

func sortedArrayToBST(nums []int) *TreeNode {
    if len(nums) == 0 {    //终止条件，最后数组为空则可以返回
        return nil
    }
    idx := len(nums)/2
    root := &TreeNode{Val: nums[idx]} 
     
    root.Left = sortedArrayToBST(nums[:idx])
    root.Right = sortedArrayToBST(nums[idx+1:])

    return root
}

JavaScript

递归

var sortedArrayToBST = function (nums) {
    const buildTree = (Arr, left, right) => {
        if (left > right)
            return null;

        let mid = Math.floor(left + (right - left) / 2);

        let root = new TreeNode(Arr[mid]);
        root.left = buildTree(Arr, left, mid - 1);
        root.right = buildTree(Arr, mid + 1, right);
        return root;
    }
    return buildTree(nums, 0, nums.length - 1);
};

迭代

var sortedArrayToBST = function(nums) {
    if(nums.length===0) {
        return null;
    }
    let root = new TreeNode(0);       //初始根节点
    let nodeQue = [root];             //放遍历的节点,并初始化
    let leftQue = [0];                //放左区间的下标,初始化
    let rightQue = [nums.length-1];   // 放右区间的下标
    
    while(nodeQue.length) {
        let curNode = nodeQue.pop();
        let left = leftQue.pop();
        let right = rightQue.pop();
        let mid = left + Math.floor((right-left)/2);
        
        curNode.val = nums[mid];      //将下标为mid的元素给中间节点
        
//         处理左区间
        if(left <= mid-1) {
            curNode.left = new TreeNode(0);
            nodeQue.push(curNode.left);
            leftQue.push(left);
            rightQue.push(mid-1);
        }
        
//         处理右区间
        if(right >= mid+1) {
            curNode.right = new TreeNode(0);
            nodeQue.push(curNode.right);
            leftQue.push(mid+1);
            rightQue.push(right);
        }
    }
    return root;
};

TypeScript

function sortedArrayToBST(nums: number[]): TreeNode | null {
    function recur(nums: number[], left: number, right: number): TreeNode | null {
        if (left > right) return null;
        let mid: number = Math.floor((left + right) / 2);
        const root: TreeNode = new TreeNode(nums[mid]);
        root.left = recur(nums, left, mid - 1);
        root.right = recur(nums, mid + 1, right);
        return root;
    }
    return recur(nums, 0, nums.length - 1);
};

C

递归

struct TreeNode* traversal(int* nums, int left, int right) {
    if (left > right) 
        return NULL;
    int mid = left + ((right - left) / 2);
    struct TreeNode* root = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->val = nums[mid];
    root->left = traversal(nums, left, mid - 1);
    root->right = traversal(nums, mid + 1, right);
    return root;
}

struct TreeNode* sortedArrayToBST(int* nums, int numsSize) {
    struct TreeNode* root = traversal(nums, 0, numsSize - 1);
    return root;
}

Scala

递归:

object Solution {
  def sortedArrayToBST(nums: Array[Int]): TreeNode = {
    def buildTree(left: Int, right: Int): TreeNode = {
      if (left > right) return null // 当left大于right的时候，返回空
      // 最中间的节点是当前节点
      var mid = left + (right - left) / 2
      var curNode = new TreeNode(nums(mid))
      curNode.left = buildTree(left, mid - 1)
      curNode.right = buildTree(mid + 1, right)
      curNode
    }
    buildTree(0, nums.size - 1)
  }
}

rust

递归：

impl Solution {
    pub fn sorted_array_to_bst(nums: Vec<i32>) -> Option<Rc<RefCell<TreeNode>>> {
        if nums.is_empty() {
            return None;
        }
        let index = nums.len() / 2;
        let mut root = TreeNode::new(nums[index]);

        root.left = Self::sorted_array_to_bst(nums[..index].to_vec());
        root.right = Self::sorted_array_to_bst(nums[index + 1..].to_vec());
        Some(Rc::new(RefCell::new(root)))
    }
}