ACM模式如何构建二叉树.md

力扣上如何自己构造二叉树输入用例？

经常有录友问，二叉树的题目中输入用例在ACM模式下应该怎么构造呢？

力扣上的题目，输入用例就给了一个数组，怎么就能构造成二叉树呢？

这次就给大家好好讲一讲！

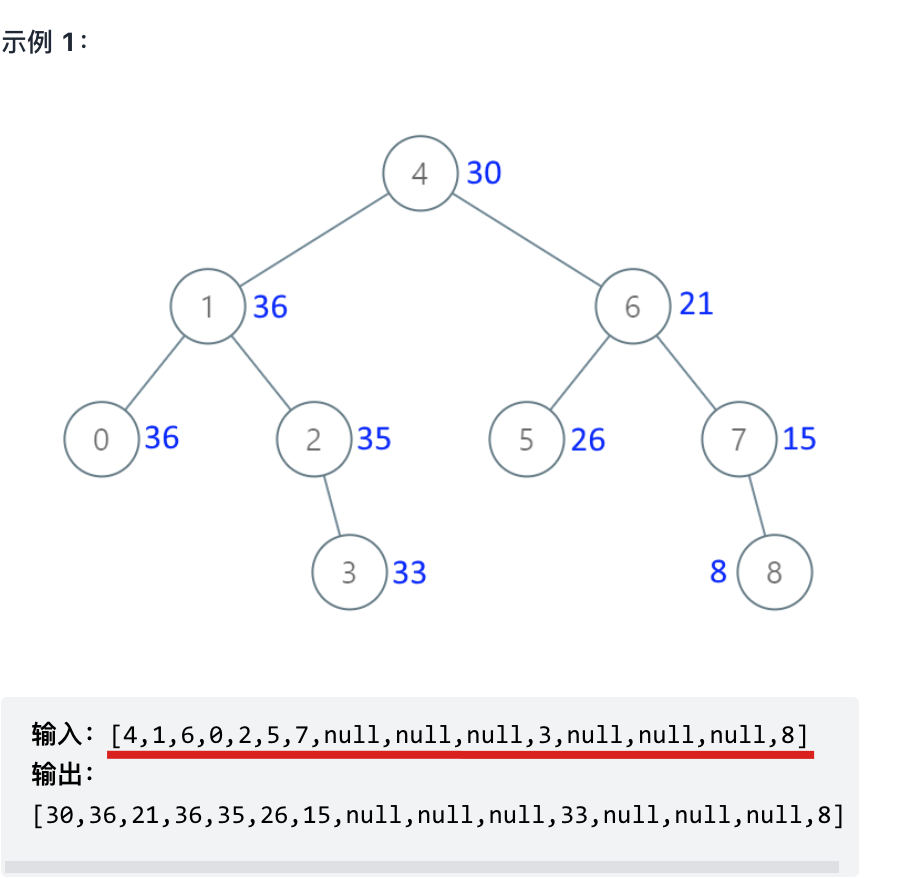
就拿最近公众号上 二叉树的打卡题目来说：

538.把二叉搜索树转换为累加树

其输入用例，就是用一个数组来表述 二叉树，如下：

一直跟着公众号学算法的录友 应该知道，我在二叉树：构造二叉树登场！，已经讲过，只有 中序与后序 和 中序和前序 可以确定一棵唯一的二叉树。 前序和后序是不能确定唯一的二叉树的。

那么538.把二叉搜索树转换为累加树的示例中，为什么，一个序列（数组或者是字符串）就可以确定二叉树了呢？

很明显，是后台直接明确了构造规则。

再看一下 这个 输入序列 和 对应的二叉树。

从二叉树 推导到 序列，大家可以发现这就是层序遍历。

但从序列 推导到 二叉树，很多同学就看不懂了，这得怎么转换呢。

我在 关于二叉树，你该了解这些！已经详细讲过，二叉树可以有两种存储方式，一种是 链式存储，另一种是顺序存储。

链式存储，就是大家熟悉的二叉树，用指针指向左右孩子。

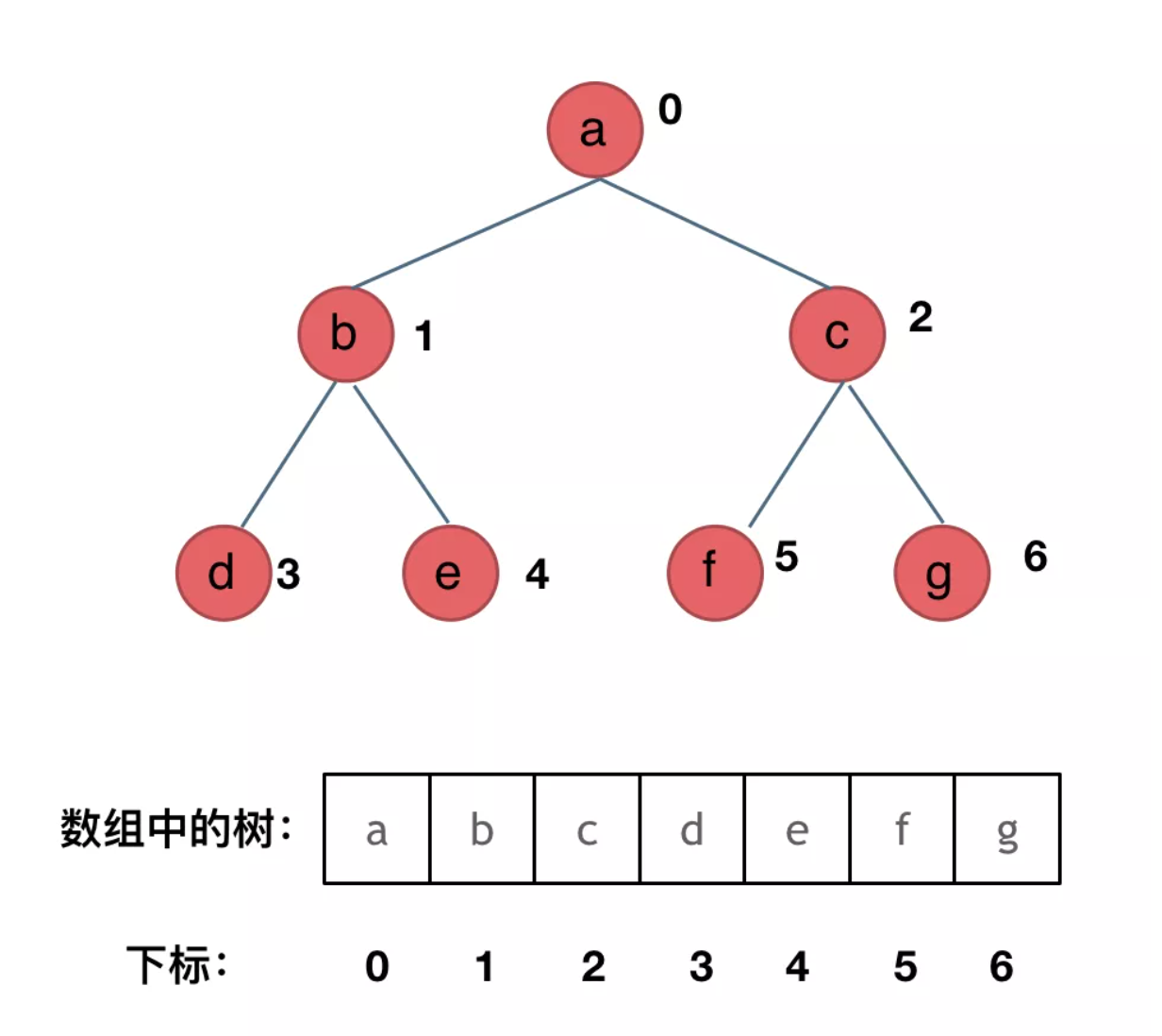
顺序存储，就是用一个数组来存二叉树，其方式如图所示：

那么此时大家是不是应该知道了，数组如何转化成 二叉树了。如果父节点的数组下标是i，那么它的左孩子下标就是i * 2 + 1，右孩子下标就是 i * 2 + 2。

那么这里又有同学疑惑了，这些我都懂了，但我还是不知道 应该 怎么构造。

来，咱上代码。 昨天晚上 速度敲了一遍实现代码。

具体过程看注释：

// 根据数组构造二叉树
TreeNode* construct_binary_tree(const vector<int>& vec) {
    vector<TreeNode*> vecTree (vec.size(), NULL);
    TreeNode* root = NULL;
    // 把输入数值数组，先转化为二叉树节点数组
    for (int i = 0; i < vec.size(); i++) {
        TreeNode* node = NULL;
        if (vec[i] != -1) node = new TreeNode(vec[i]); // 用 -1 表示null
        vecTree[i] = node;
        if (i == 0) root = node;
    }
    // 遍历一遍，根据规则左右孩子赋值就可以了
    // 注意这里 结束规则是 i * 2 + 1 < vec.size()，避免空指针
    // 为什么结束规则不能是i * 2 + 2 < arr.length呢?
    // 如果i * 2 + 2 < arr.length 是结束条件
    // 那么i * 2 + 1这个符合条件的节点就被忽略掉了
    // 例如[2,7,9,-1,1,9,6,-1,-1,10] 这样的一个二叉树,最后的10就会被忽略掉
    // 遍历一遍，根据规则左右孩子赋值就可以了
           
    for (int i = 0; i * 2 + 1 < vec.size(); i++) {
        if (vecTree[i] != NULL) {
            // 线性存储转连式存储关键逻辑
            vecTree[i]->left = vecTree[i * 2 + 1];
            if(i * 2 + 2 < vec.size())
            vecTree[i]->right = vecTree[i * 2 + 2];
        }
    }
    return root;
}

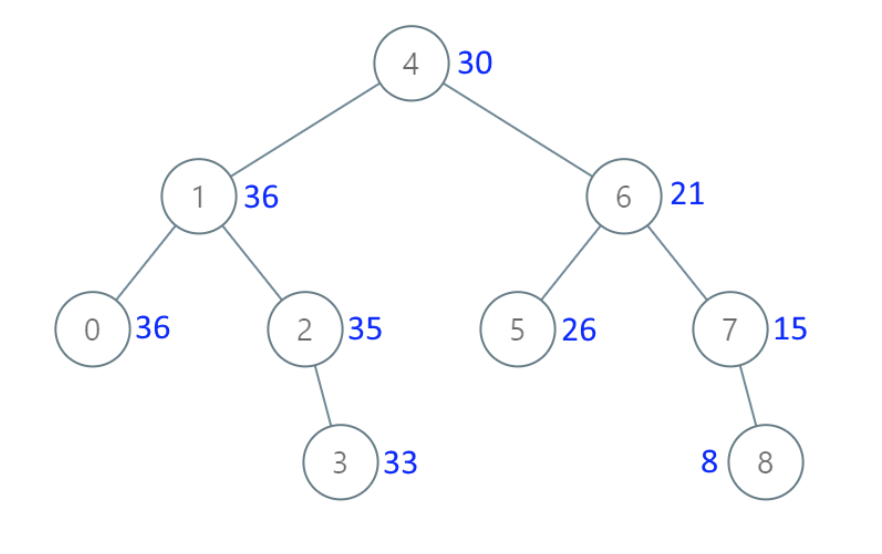
这个函数最后返回的 指针就是 根节点的指针， 这就是 传入二叉树的格式了，也就是 力扣上的用例输入格式，如图：

也有不少同学在做ACM模式的题目，就经常疑惑：

• 让我传入数值，我会！
• 让我传入数组，我会！
• 让我传入链表，我也会！
• 让我传入二叉树，我懵了，啥？ 传入二叉树？二叉树怎么传？

其实传入二叉树，就是传入二叉树的根节点的指针，和传入链表都是一个逻辑。

这种现象主要就是大家对ACM模式过于陌生，说实话，ACM模式才真正的考察代码能力（注意不是算法能力），而 力扣的核心代码模式 总有一种 不够彻底的感觉。

所以，如果大家对ACM模式不够了解，一定要多去练习！

那么以上的代码，我们根据数组构造二叉树，接来下我们在 把 这个二叉树打印出来，看看是不是 我们输入的二叉树结构，这里就用到了层序遍历，我们在二叉树：层序遍历登场！中讲过。

完整测试代码如下：

#include <iostream>
#include <vector>
#include <queue>
using namespace std;

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

// 根据数组构造二叉树
TreeNode* construct_binary_tree(const vector<int>& vec) {
    vector<TreeNode*> vecTree (vec.size(), NULL);
    TreeNode* root = NULL;
    for (int i = 0; i < vec.size(); i++) {
        TreeNode* node = NULL;
        if (vec[i] != -1) node = new TreeNode(vec[i]);
        vecTree[i] = node;
        if (i == 0) root = node;
    }
    for (int i = 0; i * 2 + 1 < vec.size(); i++) {
        if (vecTree[i] != NULL) {
            vecTree[i]->left = vecTree[i * 2 + 1];
            if(i * 2 + 2 < vec.size())
            vecTree[i]->right = vecTree[i * 2 + 2];
        }
    }
    return root;
}

// 层序打印打印二叉树
void print_binary_tree(TreeNode* root) {
    queue<TreeNode*> que;
    if (root != NULL) que.push(root);
    vector<vector<int>> result;
    while (!que.empty()) {
        int size = que.size();
        vector<int> vec;
        for (int i = 0; i < size; i++) {
            TreeNode* node = que.front();
            que.pop();
            if (node != NULL) {
                vec.push_back(node->val);
                que.push(node->left);
                que.push(node->right);
            }
            // 这里的处理逻辑是为了把null节点打印出来，用-1 表示null
            else vec.push_back(-1);
        }
        result.push_back(vec);
    }
    for (int i = 0; i < result.size(); i++) {
        for (int j = 0; j < result[i].size(); j++) {
            cout << result[i][j] << " ";
        }
        cout << endl;
    }
}

int main() {
    // 注意本代码没有考虑输入异常数据的情况
    // 用 -1 来表示null
    vector<int> vec = {4,1,6,0,2,5,7,-1,-1,-1,3,-1,-1,-1,8};
    TreeNode* root = construct_binary_tree(vec);
    print_binary_tree(root);
}

可以看出我们传入的数组是：{4,1,6,0,2,5,7,-1,-1,-1,3,-1,-1,-1,8} ， 这里是用 -1 来表示null，

和 538.把二叉搜索树转换为累加树 中的输入是一样的

这里可能又有同学疑惑，你这不一样啊，题目是null，你为啥用-1。

用-1 表示null为了方便举例，如果非要和 力扣输入一样一样的，就是简单的字符串处理，把null 替换为 -1 就行了。

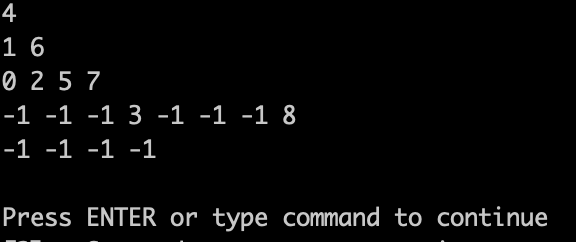
在来看，测试代码输出的效果：

可以看出和 题目中输入用例 这个图 是一样一样的。 只不过题目中图没有把 空节点 画出来而已。

大家可以拿我的代码去测试一下，跑一跑。

注意：我的测试代码，并没有处理输入异常的情况（例如输入空数组之类的），处理各种输入异常，大家可以自己去练练。

总结

大家可以发现，这个问题，其实涉及很多知识点，而这些知识点 其实我在文章里都讲过，而且是详细的讲过，如果大家能把这些知识点串起来，很容易解决心中的疑惑了。

但为什么很多录友都没有想到这个程度呢。

这也是我反复强调，代码随想录上的 题目和理论基础，至少要详细刷两遍。

**知识星球**里有的录友已经开始三刷：

只做过一遍，真的就是懂了一点皮毛， 第二遍刷才有真的对各个题目有较为深入的理解，也会明白 我为什么要这样安排刷题的顺序了。

都是卡哥的良苦用心呀！

其他语言版本

Java

public class Solution {
    // 节点类
    static class TreeNode {
        // 节点值
        int val;
        
        // 左节点
        TreeNode left;

        // 右节点
        TreeNode right;

        // 节点的构造函数(默认左右节点都为null)
        public TreeNode(int x) {
            this.val = x;
            this.left = null;
            this.right = null;
        }
    }
    
    /**
     * 根据数组构建二叉树
     * @param arr 树的数组表示
     * @return 构建成功后树的根节点
     */
    public TreeNode constructBinaryTree(final int[] arr) {
        // 构建和原数组相同的树节点列表
        List<TreeNode> treeNodeList = arr.length > 0 ? new ArrayList<>(arr.length) : null;
        TreeNode root = null;
        // 把输入数值数组，先转化为二叉树节点列表
        for (int i = 0; i < arr.length; i++) {
            TreeNode node = null;
            if (arr[i] != -1) { // 用 -1 表示null
                node = new TreeNode(arr[i]);
            }
            treeNodeList.add(node);
            if (i == 0) {
                root = node;
            }
        }
        // 遍历一遍，根据规则左右孩子赋值就可以了
        // 注意这里 结束规则是 i * 2 + 1 < arr.length，避免空指针
        // 为什么结束规则不能是i * 2 + 2 < arr.length呢?
        // 如果i * 2 + 2 < arr.length 是结束条件
        // 那么i * 2 + 1这个符合条件的节点就被忽略掉了
        // 例如[2,7,9,-1,1,9,6,-1,-1,10] 这样的一个二叉树,最后的10就会被忽略掉
        for (int i = 0; i * 2 + 1 < arr.length; i++) {
            TreeNode node = treeNodeList.get(i);
            if (node != null) {
                // 线性存储转连式存储关键逻辑
                node.left = treeNodeList.get(2 * i + 1);
                //  再次判断下 不忽略任何一个节点
                if(i * 2 + 2 < arr.length)
                node.right = treeNodeList.get(2 * i + 2);
            }
        }
        return root;
    }
}

Python

class TreeNode:
    def __init__(self, val = 0, left = None, right = None):
        self.val = val
        self.left = left
        self.right = right


# 根据数组构建二叉树

def construct_binary_tree(nums: []) -> TreeNode:
    if not nums: 
        return None
    # 用于存放构建好的节点
    root = TreeNode(-1)
    Tree = []
    # 将数组元素全部转化为树节点
    for i in range(len(nums)):
        if nums[i]!= -1:
            node = TreeNode(nums[i])
        else:
            node = None
        Tree.append(node)
        if i == 0:
            root = node
    # 直接判断2*i+2<len(Tree)会漏掉2*i+1=len(Tree)-1的情况
    for i in range(len(Tree)):
        if Tree[i] and 2 * i + 1 < len(Tree):
            Tree[i].left = Tree[2 * i + 1]
            if 2 * i + 2 < len(Tree):
                Tree[i].right = Tree[2 * i + 2]
    return root



# 算法:中序遍历二叉树

class Solution:
    def __init__(self):
        self.T = []
    def inorder(self, root: TreeNode) -> []:
        if not root:
            return 
        self.inorder(root.left)
        self.T.append(root.val)
        self.inorder(root.right)
        return self.T



# 验证创建二叉树的有效性,二叉排序树的中序遍历应为顺序排列

test_tree = [3, 1, 5, -1, 2, 4 ,6]
root = construct_binary_tree(test_tree)
A = Solution()
print(A.inorder(root))

Go

package main

import "fmt"

type TreeNode struct {
    Val   int
    Left  *TreeNode
    Right *TreeNode
}

func constructBinaryTree(array []int) *TreeNode {
    var root *TreeNode
    nodes := make([]*TreeNode, len(array))

    // 初始化二叉树节点
    for i := 0; i < len(nodes); i++ {
	var node *TreeNode
	if array[i] != -1 {
	    node = &TreeNode{Val: array[i]}
	}
	nodes[i] = node
	if i == 0 {
	    root = node
	}
    }
    // 串联节点
    for i := 0; i*2+2 < len(array); i++ {
        if nodes[i] != nil {
	    nodes[i].Left = nodes[i*2+1]
	    nodes[i].Right = nodes[i*2+2]
	}
    }
    return root
}

func printBinaryTree(root *TreeNode, n int) {
    var queue []*TreeNode
    if root != nil {
	queue = append(queue, root)
    }

    result := []int{}
    for len(queue) > 0 {
	for j := 0; j < len(queue); j++ {
	    node := queue[j]
	    if node != nil {
		result = append(result, node.Val)
		queue = append(queue, node.Left)
		queue = append(queue, node.Right)
	    } else {
	        result = append(result, -1)
	    }
        }
	// 清除队列中的本层节点, 进入下一层遍历
	queue = queue[len(queue):]
    }
    
    // 参数n控制输出值数量, 否则二叉树最后一层叶子节点的孩子节点也会被打印(但是这些孩子节点是不存在的).
    fmt.Println(result[:n])
}

func main() {
    array := []int{4, 1, 6, 0, 2, 5, 7, -1, -1, -1, 3, -1, -1, -1, 8}
    root := constructBinaryTree(array)
    printBinaryTree(root, len(array))
}

JavaScript

---