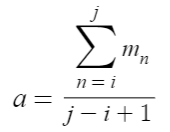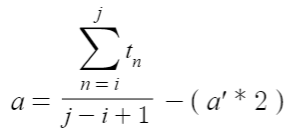AdditionOfTheNextCandidateBlock.md

After the mathematical verification of the algorithm, I wanted to proceed with the implementation phase, but I will briefly show the actual operation method so that more people can understand the algorithm. I originally tried to prepare a screen that could be simulated briefly for the default behavior. However, because this project is not my main work, I could not prepare the screen in time. First of all, I will write about the details of the required design parts first, so that anyone who understands the algorithm can implement it.

Through the initial project main page, I showed the basic consensus method of the new blockchain algorithm. The contents of the main formulas for the consensus have been explained, but the algorithm has not been analyzed probabilistically, and the necessary relation formulas or probability formulas have not been defined from them.

A value with randomness generated from the hash function is used for the consensus and the subsequent stochastic process also takes the form of a random walk. The difficulty is used for the random variable and the number of the next candidate blocks that satisfy it follows the probability distribution. This algorithm can be defined as a probability theory and the relevance of a candidate block chain can be defined as Shannon entropy. Starting from the highest entropy, the consensus continues until the highest information gain corresponding to the lowest entropy occurs.

The entire operation of the algorithm must be described as a probability formula and each base value of the algorithm must be derived from it. In order to be treated as such a mathematical probability, it has to be submitted as a thesis and needs to be verified and continued research by the academic community, but has not yet been progressed. Due to personal circumstances, I do not have any plans at this time. Like many other consensus algorithms, it will be implemented first as a test net and it will be accessed as an empirical probability.

To construct a test net, all the structural parts to make a single system must be designed. It should include the selection of the base values ​​used in the algorithm, the generation of the initial genesis block, and the information propagation method, as well as the structure of the operation and management of the network and the structure for reflecting the new policy. In detailed design, there should be no parts by which the security could be threatened such as the violation of confidentiality or authentication process and the leakage of information that could be an attack target, and there should be no sections where distributed denial-of-service attacks using the characteristics of the distributed system are possible. To ensure that the game theory, which is the basis of the blockchain, should be effective in all operations, there should be no problems such as 'nothing at stake'. It is designed so that localization does not occur in accordance with the basic purpose of decentralization, and additionally equality of opportunity is achieved.

A new way to solve scalability problem, or at least the preparation for that, should be included as a structure. As a structure for scalability, I am considering a way to use distributed chains of tree structure together with the current consensus method. It is a structure that does not converge or partially converges the branched chains, but I have not yet designed the parts related to how to distribute the authentications or how to conserve the chains. It is different from DAG(directed acyclic graph). It may not be included in the first implementation, but will include relevant sections for future expansion.

This algorithm is aimed at a fully autonomous network. In order to do this, it must be able to respond to not only failures and exceptions, but also the expansion and reduction of network, and the level of security required. As a first application, in order to deal with the failure situation and the scale change of network, the algorithm itself detects the state of the network, it responds actively and adapts accordingly. This part is covered in this issue document.

I am aiming to be created a complete system, but this project is still going on by myself. So, I am filling out the necessary parts with the new issue document on the main project page. In some cases, while proceeding in detail, contents may be changed or new contents may be added. In some cases, a detailed functional objective may be proposed in various ways. This project is going on in my spare time, so it is progressing slowly. At first, I am showing some detailed design through this issue document and the next issue document so that it can be simulated by simple code implementation before testnet.

In this algorithm, a block to be issued authentication for the ledger is selected before the authentication request for the ledger occurs. To this end, a candidate block chain is operated and a consensus is reached over a large number of candidate blocks over a long period of time. The time and spatial performance of this algorithm are determined by how this candidate block chain operates. The chains, which are subject to main discussion in this and the following documents, mentioned in the rest of this document are all candidate block chains. All the blocks mentioned hereafter also stand for candidate blocks.

The relevance calculation formula used in the consensus shown in the main document actually works for two cases. One is when a block and a block meet, and the other is when a chain and a chain meet. The case where a chain meets a chain includes the case where a block and a chain meet. This is described in the next issue document on "Synchronization of chain information" as the process of converging branched chains. All nodes in the network issue a new block for one chain branch selected at each node. This is the main chain of each node, and each node negotiates based on the block with the largest sequence number in the chain. When a block and a block meet, it is a competition situation when a new block is added to this main chain. In the relevance calculation formula, since the c value at this time is 1 and there are no following blocks, so they compete only with their self-relevance of 2 ^ m. This competition situation is covered in this issue document, and in relation to that, the average relevance and the average transmission time are explained in terms of probability. Through this, localization is explained, and a technique that prevent the localization is showed.

A large number of opinions come together to create a policy which is reflected to set target values such as time performance, spatial performance and security property of the system. To satisfy these target values, base values ​​such as algorithm's difficulty, relevance factor, relevance efficiency ratio, threshold value, and time base for flow control are adjusted. The status values, which can be used to check the status of the current network, are used as information for adjusting these base values, and the state values include the self-relevance of each block, the average relevance of each segment in the chain, the relative transmission time of each block, the average transmission time of each segment in the chain, the last authentication block and the first or last candidate block, etc. In the end, all these values will be automated as a function of the system, but first I will use some status values ​​to adjust the difficulty and time base, so I will show a detailed design that can bring out the performance that can be commercialized first.

Due to the nature of the hash function used in cryptographic application, the hash values ​​of the blockchain have a high level of randomness, and there is no correlation between the hash values ​​of adjacent blocks. Therefore, the number of possible cases of hash values generated from a large number of nodes is evenly distributed. When the enough randomness is based, the smallest values that can be distributed to two nodes are two values ​​of 0 or 1, so there is no collision for the hash values of 1-bit length. The smallest values that can be distributed to four nodes are four values ​​of 0, 1, 2, or 3, so there is no collision for the hash values of 2-bit length. The smallest values that can be distributed to 2 ^ n nodes are 2 ^ n values ​​from 0 to (2 ^ n) - 1, so there is no collision for the hash values of n-bit length. Of course, this is probabilistic but very effective because of the cryptographic characteristic based on the randomness of uniform distribution and the characteristic of large-scale distributed system. This algorithm also contains proprietary information as input to the hash function. By design so far, a new block does not contain time information. In the main document, it has been described that the information of the finally confirmed authentication block is included in the next block to be newly created, but it is also excluded from the first implementation. Therefore, the proprietary information is the only distinguishable value among the input values of the hash function in the competition for the next block, and it is also a distinct value that uniquely identifies each node in the entire network. In nodes with the same main chain, the hash value of the previous block is the same for all nodes, but the proprietary information is unique for each node, so the newly created hash value through the hash function is also unique for each node. Because of these characteristics, the network can have the number of bits for random numbers that do not cause a collision in proportion to the total number of nodes. If there are two nodes, the network can have 1-bit random numbers that do not cause a collision. If there are four nodes, the network can have 2-bit random numbers that do not cause a collision. If there are 2 ^ n nodes, the network can have n-bit random numbers that do not cause a collision.

On the contrary, it is possible to estimate the number of nodes in the current network through the length of bits that match a particular value. One particular value is not a fixed value. By randomly choosing a number from a n-bit random number that does not cause a collision, it makes equality of opportunity by choice of algorithm rather than effort. The hash value of the previous block is used as a specific value, and its value changes unpredictably for each competition. A competition takes place with the new hash values generated at each node and the number of consecutive bits that match the hash value of the previous block at each node. If there are two nodes, there is one node that matches one bit with the hash value of the previous block. If there are four nodes, there is one node that matches two bits with the hash value of the previous block. If there are 2 ^ n nodes, there is one node that matches n bits with the hash value of the previous block. To select one of the blocks generated by 2 ^ n nodes, it can be expressed as lb( 2 ^ n ) shannon bit using a binary log with base 2, and from this, n bits can be obtained. Although the above is expressed mathematically, it will be described in a way that explains the basic principles so that as many people as possible can understand the algorithm than mathematical notation in this document as well as future documents.

Most of the contents described through the articles added as an issue, including this one, is intended to help you understand the basic consensus algorithm on the project main page. Continuing below, some detailed techniques that are not included in the base document may be introduced, but the basic design of the algorithm does not change. It is not easy to understand the whole probability process for the whole cycle of the chain at a time. As a distributed system based on probabilistic estimation, all operations are correlated and concurrent. The purpose of the issue documents is to show this one probability process that operates over the whole time and space by showing the spatial structure and the time structure to help the understanding of this algorithm.

As shown above, we can estimate the number of nodes present in the current network through the number of bits that match the hash value of the previous block selected through consensus. It is a probabilistic estimate, not an exact measurement of any one moment. Based on this, statistics from the chain are used in the actual implementation.

The number of nodes in the network increases or decreases over time. We can detect a quantitative change of nodes through the matching number of hash bits, and by reflecting this in the algorithm, we can make the algorithm adapt itself to the change of the network. This information can be obtained from the chain, and it can be reflected back into the chain. This allows us to control the base values of the algorithm to maintain the desired target values at a certain level.

Each node, using their chain information, can calculate the arithmetic mean of the number of consecutive matching hash bits for each candidate blocks.

n : sequence number
i : sequence number of first candidate block
j : sequence number of last candidate block
m : number of consecutive bits with the same value as the previous hash value starting from the beginning
a : average of consecutive hash bits with the same value

This value is the average relevance that represents the self-relevance of each block on a node. From this average relevance, we can estimate the number of nodes in the recent network. It is an estimate, not a measurement. In the self-relevances of the actual chain, the distribution of the values of the upper and lower blocks is different. Therefore, in actual implementation, the ratio for it is applied and used. By using this average relevance again as a difficulty for the next block generation, we can control the degree of branching in the chain that can occur in the next competition.

Average relevance is the average of the number of nodes in the network, which meet the threshold over a time interval. Based on such values as the relevance factor or threshold that are assumed in the text, even if small, 1000 to 10000 blocks are used as a sample for average relevance. This time interval is the time it takes for the newly added candidate block to issue the authentication, and it will be several hours even if it is a short time based on the network shown in the text. Changes in network size or target value affect the number of blocks for which the threshold is filled or the time interval before issuing the authentication. The blockchain in which this algorithm is used assumes a network that slowly grows or declines by voluntary participation, rather than a network that bulks up or shrinks at a time by control. Since the statistics for the above time interval are used, if there is a sudden change in the network scale, the chain gradually adapts to the changed network scale even if there is a difference in some time.

Average relevance changes little by little whenever the first candidate block changes to an authentication block or whenever new candidate block is added. Also, the average relevance at each node is not exactly the same at any one moment. These change probabilistically with the degree to which the chain branches, but the difference is not large because the branches in the chain are made during the same time interval in each regional network. As a result, the difficulty is also not fixed in all times and space of each time, so its value is not included in the creation of a new block. In all blocks, only the minimum information that can be validated explicitly is included as data. Difficulty is a value that is calculated from values that represent the state of the current chain, and it is a relative value that is calculated and maintained at each node itself. Rather than being used as a way to exchange real information and share consistent information, probabilistic values that are consistently estimated by the same calculation method are used. Target values, base values and status values, which are covered in this algorithm, are managed in this way.

Difficulty is used as a base value for the eligibility to create the next candidate block. If no difficulty is used, all nodes are eligible to create the next candidate block. However, due to the consensus process that continues over a long period of time, most of the blocks with low self-relevance are dropped out of the early competition. The former purpose of the difficulty was to reduce the wasteful branching of the chain from such unnecessary competition and thereby increase the efficiency of the network. From here, however, we control the degree of branching in the chain using dynamically adjusted difficulty. The degree of branching in the chain is proportional to the speed at which the authentication is issued, and this is related to the localization that will be explained in the latter part. However, if it goes beyond a certain level, there will be overloads in the management of the branched chains and bottlenecks in the network. As a further discussion to be discussed later, at the turning point of these relationships, performance can be maximized. Like this, the performance of the chain can also be adjusted by the difficulty controlled dynamically. Even so, values like relevance factor or threshold are the direct and most significant base values for the speed at which authentication is issued. The dynamically controlled difficulty regulates the spatial performance of the network and the chain at any point in time.

The difficulty for the next candidate block is calculated by subtracting a certain number of bits from the average relevance. This certain number of bits is shannons(Shannon's Bits) that controls the degree of branching of the chain and it is used as a branch quotient.

a : average of consecutive hash bits with the same value (a >= 0)
b : branch quotient in bits (b <= a)
d : number of difficulty bits (d <= a)

d = a - b

If 0 is used as the branch quotient, only one node can generate the next block, so no chain branch occurs. If 1 is used as the branch quotient, two nodes can generate the next block, so two chain branches can occur. If 2 is used as the branch quotient, four nodes can generate the next block, so four chain branches can occur. If b is used as the branch quotient, 2 ^ b nodes can generate the next block, so 2 ^ b chain branches can occur. However, in a real network, branching can occur in the chain even if 0 is used as the branch quotient. All of the above values ​​can be predicted with probability in the most ideal situation. With respect to the degree of branching of the chain, the state value measured more closely to the actual rather than the predicted is covered in the next issue document, but the value is also probabilistic.

In a uniformly distributed network, the hash values ​​of the next block created by each node are uniformly distributed. The next block that can be added to the chain in the entire network is decisively chosen based on the random nature of the cryptographic algorithm. As a result, the nodes that can add the next block to the chain are already decided and uniformly distributed in the network space. Due to the time difference for newly created blocks to propagate to other nodes, each node that issues a new block has its own zone. These nodes, which are uniformly distributed in the network, have a uniform distance from each other, so the zone of each node also has a uniform size. So far, this has not been an effort, but an algorithmic selection, so it does not cause localization. However, the activeness for quick participation causes temporary localization by the next block which is chosen as a locally uniform distribution. For faster processing speed in this algorithm, more opportunities are given to nodes that more quickly and actively participate in the consensus. As one of the game theories on which this algorithm is based, this is to allow the algorithm to work permanently without stopping. Cumulative relevance is used for the branched chains that result from this, and consensus is reached through a continuous convergence process. In some cases, the activeness for quick participation can be seen as an effort, and the ratio of this effort is adjusted by the algorithm's base values.

Like the branches of chain, the division of the network into zones is also a positive function that the algorithm allows. Because of the branches of the branched chain, the network is divided into zones. The network that can be excessively expanded is layered on a regional basis and then managed efficiently. Allowing branching of the chain causes spatial performance and synchronization issues, and the algorithm controls those. The existence of zones likewise causes localization problem, which are also controlled by the algorithm. This is explained in the following contents and in the following issue documents.

Due to the difference in transmission time between each node, the network is divided into as many zones as the number of branches in the chain. If two nodes, which can add the next block, are selected because of branch index 1, the entire network space is divided into two zones. If four nodes are selected because of branch index 2, the entire network space is divided into four zones. If 2 ^ b nodes are selected because of branch index b, the entire network space is divided into 2 ^ b zones. Localization due to the equally sized zones and the activeness for quick participation causes again branching in each branched chain, and the number of branches in the whole chain increases exponentially. When localization exists, the exponential growth of the chain can cause the given network space to continue to be divided internally into smaller zones. The space could be divided in a fractal pattern, and the fractal dimension as the division ratio at that time would be the branch quotient. As the size of a zone gets smaller, the number of nodes belonging to each zone also decreases. This not only makes the wealth more biased, but also causes the relative frequencies of occurrence of each of the events in the probability space to decrease exponentially, so it weakens the underlying logic of the algorithm based on probabilistic estimates. However, this self-similarity is avoided by using the average relevance of all the blocks in the candidate block chain, not the self-relevance of the immediately preceding block. In addition, the control of the transmission time works together, so space is not internally divided. Spatial partitioning in situations where another branch occurs from one branch is handled later in this document, where the discussion of time control proceeds. In addition to the use of average relevance, techniques to resist the probabilistic errors, which are described later, and to prevent the localization are also used as preemptive systems. Also, at the same time as the branching of the chain, the branched chains are converged into a single chain through continuous consensus. Due to the simultaneous progression of branching and convergence, the number of branches in the entire chain becomes a race condition situation and the spatial performance of the chain changes fluidly. The degree of the situation is controlled by the base values of the algorithm but is also affected by the frequency of authentication requests for ledgers corresponding to external factors. Until the threshold is filled, the chain continues to branch and to converge. However, after the threshold is satisfied, there is no addition of a new block until a new authentication block for the new ledger is issued. As a result, branching of the chain no longer occurs and only convergence continues. This is a preventive system against the number of branches of the chain that can exceed the maximum level unexpectedly. The suppressive system for this is covered in the convergence of the branched chain of the next issue document. To be described in the following issue document, split transmission is performed at a fixed time interval with respect to the unit of a bundle of blocks in order to synchronize the branched chains. To do this, dynamic buffering is performed on each node, and it determines the spatial performance of the chain along with the degree of network load. The size of the bundle, the time interval, and the size of the buffer are also dynamically adjusted from the state of the current chain. This is related to the prevention of distributed denial-of-service attacks and is discussed in more detail in the following document.

As shown above, when the branch quotient becomes smaller, the number of branches of the chain decreases and the spatial performance increases, and when the branch quotient becomes larger, the number of branches of the chain increases and the spatial performance decreases. However, time performance works in reverse. When the number of zones decreases as the branch quotient becomes smaller, the area occupied by one zone in the entire network becomes larger. One zone is the basic unit area where one consensus is made. Because of the enlarged zone, the distance for one block to be transmitted becomes longer and the transmission time for one consensus increases. This lowers the speed at which blocks are added to the chain and makes the time for the threshold to be satisfied to be longer. Like this, we need to use a large branch quotient to increase the speed of authentication issuance, but a small branch quotient to prevent unnecessary resource waste of the system due to unnecessary branching of the chain. In this regard, there are three ways to use the branch quotient. So far, it has been a way to use the difficulty that changes dynamically in proportion to the dynamically changing average relevance ​​while using fixed branch quotient based on policy. Even though the network grows, the branch quotient is fixed, so the total number of zones and the spatial performance of the chain is fixed. Instead, since the size of the area occupied by one zone increases, the transmission time for one consensus gets longer, and the time performance of the chain is consequently reduced. This method can be considered in a low-power network such as IoT environments where the spatial performance of the network is relatively important, but it is not used in networks with normal environments. Another way is to use the branch quotient that changes dynamically in proportion to the dynamically changing average relevance while using fixed difficulty based on policy. In this method, since the difficulty is fixed, the number of nodes for one zone is fixed and the size of each zone does not change. So, even if the network scale increases, the time performance of the chain is kept constant. However, since the branch quotient of the chain changes dynamically, if the network scale increases, the branch quotient increases, so the total number of zones increases and the spatial performance decreases. As the last is a compromise between the first and the second shown above, it is a way that both values change together in proportion to the average relevance while maintaining a constant ratio of the branch quotient and difficulty. In this case, as the network size increases, the time performance and the spatial performance decrease together at a certain rate which has a smaller variation compared to the above two methods. In the first implementation, the second or third method will be applied. As we can see from the above, the performance of the chain decreases as the network size increases. It's just a look at the effect of performance on the branch quotient and difficulty, but the actual speed at which authentications are issued is more directly affected by relevance factor and threshold than the above. The higher the difficulty, the faster the threshold would increase. The larger the network becomes, the more secure the algorithm becomes, and the probabilistic nature of the algorithm becomes also more effective. As a result, the performance of the chain increases because smaller values such as relevance factor or threshold can be used. Although the actual methods by which the other reference values are managed have not yet been shown, they are also dynamically adjusted from the state of the chain. Based on the desired target values, the algorithm always keeps the chain at a consistent state. To do this, the algorithm adjusts the base values using the status values of the current chain. As one of these status values, the chain also has an average transmission time in addition to the average relevance, and these two values are used in the consensus when two blocks meet.

The scale of a network can be described in terms of time and space. There are nodes distributed in a network and there are transmission times among these nodes. This transmission time is influenced not only by the topological distance but also by the quality of the transmission medium or the control by policy. When a new block is added to the chain, the algorithm uses the time difference between this block and the immediately preceding block as the transmission time. This transmission time includes the time that a node used to create the new block just before the block was sent to the network. Like self-relevance, this value is also measured and used by itself at each node, so that information is not included in any block.

Each node keeps track of the transmission time when the first block corresponding to each sequence number is added to its own chain which is managed asynchronously by each of them. Each node can calculate the actual average transmission time for the last candidate block from its own arithmetic mean of each transmission time recorded for each candidate block.

n : sequence number
i : sequence number of first candidate block
j : sequence number of last candidate block
t : transmission time of candidate block
a' : average transmission time for the immediately previous candidate block
a : average transmission time for the last candidate block

In case the average transmission time is implemented using a simple arithmetic mean, it is equal to the value calculated by dividing the time difference between the arrival of the first candidate block and the last candidate block by the total number of candidate blocks. In both cases, the actual average transmission time for the last candidate block is calculated by subtracting double the average transmission time used for the immediately previous candidate block. This subtracted time value is the zone transmission time, which is created by the rules of the algorithm to prevent localization. A zone is a basic unit area on the network space where one next candidate block can be created, and it is the smallest area where one next consensus can proceed. The average transmission time is the average value of the time at which a new block created by a node in the middle of a zone is transmitted to all other nodes in the zone. When the nodes are uniformly distributed in the network, it takes twice as long as the average transmission time for a block to reach its zone boundary, and this is the zone transmission time. By using this time value, the inside and outside of a zone are distinguished, and the localization is prevented. A zone and all surrounding zones immediately adjacent to that zone have topological differences in one absolute topological space that covers the entire network range. By changing this, based on a target zone, it makes nodes compete in each relative topological space that scopes a new space containing areas that are half of all the zones immediately adjacent to the target zone. To create each new virtual topological space based on each zone, the next block issued from each zone has a time delay corresponding to the previous zone transmission time. The techniques for creating and using this time delay are continuously described in the following contents. Because of the zone transmission time, in order for a block to be added in a zone, it takes three times as much time to transfer a packet over the real physical network corresponding to that zone. As this delay is applied, the actual value obtained in the above equation is the actual average transmission time for general packets in a zone. By multiplying the average transmission time on this zonal scale by the total number of zones corresponding to the branch quotient, the average transmission time on a scale of the entire network area can be calculated. This value is also used for the convergence of the branched chain, which is the next issue document.

As with the average relevance, the average transmission time also uses an arithmetic mean. If the algorithm is further analyzed from a statistical point of view, other types of representative values such as median or mode may be used. If there is a node with a transmission medium, which has a very low quality, at a very long distance from the center of the network, it may be handled differently by policy.

In order to obtain the arithmetic mean, the heaviest calculation for creating a new candidate block is a process of calculating a single value using all the candidate blocks as a population. If we look deep into the candidate block chain only, it is like a queue. When the leader block is about to be consumed as a new authentication block, one block is removed from the exit of the candidate block chain. When a new candidate block is about to be added, one block is added at the entrance of the candidate block chain. In the actual implementation, the logic will be prepared to operate on only one block that is to be added or excluded. This minimizes the execution time of the program code that prepares the next candidate block in the node. PoR(proof-of-relevance) does not perform time-consuming operations such as PoW(proof-of-work). It does not make a difference in execution time between low-performance nodes in IoT environment and high-performance nodes with high clocks. Parallelization is also meaningless for one proprietary information. Because the execution time on a node can be ignored, the average transmission time includes this. If other parts of the algorithm also require time-consuming logic in which preprocessing or deferred processing is not possible, then more space would be adopted. To do this, even a low-cost node may require some amount of storage space. This is also necessary for the caching of chain branches in relation to the synchronization topic of the next issue document. However, the contents of this document were already written in Korean a month ago and now it is being translated into English. During that one month, the design for synchronization of the chain information has changed, and caching is no longer necessary.

The average relevance and the average transmission time are used to reflect the size of space and time of the network. As the difficulty is changed, the spatial and time performance of the network are exclusively correlated. Using the average relevance and the average transmission time, the chain adapts to changes in scale to the network. In addition to these, the sequence number is used to synchronize the chain. The genesis block, which is first issued, uses sequence number 0. Blocks following the genesis block have sequence numbers that increment by one, starting with one. The following sections will show the procedure for sending and receiving one candidate block using all of these. Through the procedure in which a new block is added to the main chain of each node, we can see the chain adapting to the network. New blocks corresponding to chain branches other than the main chain are also received, but the procedure for receiving them is not explained here. Details related to this are covered in the next issue document, "synchronization of branched chains".

To add the next block to the chain, all nodes create a new block by computing a new hash value containing the hash value of the immediately previous block and its own proprietary information. When the relevance of the hash value of the immediately preceding block and a new block at a node is equal to or greater than the difficulty of the current chain, the node adds the new block as the next block and sends it to the network. The node issuing the new block writes the block's transmission time as the current zone transmission time rather than zero. When the relevance of a new block at a node is less than the difficulty, the node waits to receive the next block created by other nodes. However, the node does not discard the new block created by itself until it receives the next block and adds it to the chain. If the node does not receive the next block until twice the zone transmission time of the current chain has elapsed since the last block was received, it lowers the current difficulty by one bit and reconfirms the relevance of the new block previously created by itself with the new difficulty. If the difficulty is met, the new block of the node is sent as the next block, otherwise it will wait again. If the next block does not arrive until twice the zone transmission time has elapsed since the node started to wait again, it lowers the difficulty once again by one bit and repeats the same process. This process continues until the difficulty becomes zero bit and is performed identically on all nodes. When the difficulty becomes zero, all nodes can issue the next block. The difficulty, in which the number of nodes in the current zone is reflected, is a probabilistically generated value, so in the worst case, the above case may also occur. By lowering the difficulty by one bit, nodes corresponding to twice the previous nodes, from two nodes to four and eight nodes, can have the opportunity to issue the next block in preparation for the probabilistic error. When the next block from other node is received and added to the chain, the node recalculates the difficulty and the average transmission time with the updated chain and repeats this process again for the block with the next sequence number.

The difficulty that was temporarily lowered by the probabilistic error is not used identically as the difficulty for the next block. As a representative value for all candidate blocks, the difficulty is recalculated each time. However, the low relevance of the newly added block is reflected even slightly to the next difficulty being recalculated. The chain gradually adapts to the changes in the network size. The increasing average transmission time is also reflected in the same way. However, this is debatable, so it would be covered again later.

The difficulty is used differently when sending and receiving blocks. When a node is receiving a block, the difficulty starts from the beginning with the adjusted difficulty which is increased by 1 bit from the current difficulty. When the zone transmission time elapses from the start time at which the immediately preceding block was added to the chain, the difficulty is reduced by 1 bit. Thereafter, it continues to be lowered by 1 bit every two times over the zone transmission time from the immediately preceding time when the difficulty was lowered by one bit. As with sending, this procedure continues until the difficulty reaches 0. Compared to the difficulty in sending, the difficulty in receiving is lowered with the time delayed by the zone transmission time. This prevents the localization. However, all nodes receive the next candidate block from the network based on the difficulty in sending. When the relevance of the received block is smaller than the difficulty in receiving and greater than or equal to the difficulty in sending, it is stored temporarily in the buffer. The difficulty in actual receiving is the difficulty in reaching a consensus to add the next candidate block to the chain.

Here is an example network configuration to show the situation where the next candidate block is added to the chain, and we can see the procedure of receiving a block through this. There are three nodes of N1, N2, and N3 in the network that belong to the same chain branch. Currently, this chain branch has D, D + 1 and T values respectively for the difficulty in sending, the difficulty in receiving, and the zone transmission time. N2 is in the same zone as N1 with a distance corresponding to T * 0.3 time. N3 is in other zone adjacent to N1 with a distance corresponding to T + ( T * 0.1 ) time.

The following is an example that the difficulty is applied to the network configured above. The difficulty of the newly created blocks in N1 and N3 is smaller than the difficulty, D, for sending, so the two nodes are waiting to receive the new block created by other nodes. The relevance of the block created in N2 is the same D value as the difficulty. Because the block satisfies the difficulty, N2 adds the block created by itself to its main chain. Also, because the new block was created at the same time as the immediately previous block was received, the actual transmission time of this block is zero. However, in order to prevent the localization, since the transmission time of all blocks is set to the zone transmission time as the minimum transmission time, the zone transmission time T of the immediately previous block is recorded as the transmission time instead of zero. After completing this process, N2 sends the new block to the network. As one of the rules not mentioned in the text, two blocks with the same proprietary information can not be added contiguously in one chain branch. A node can not add its own blocks to its chain in succession. Therefore, N2 can not create the next block in succession, so it waits to receive blocks created by other nodes. N2's block arrives at the adjacent N1 first. The relevance of the received block is equal to D which is the relevance for sending, but it is smaller than D + 1 which is the difficulty for receiving, because not yet a time T has elapsed, so N1 temporarily stores this block in its buffer. When the time corresponding to the zone transmission time T has elapsed since the block was stored in the buffer, this stored block is taken out of the buffer and the consensus for the block proceeds. Since N2 has sent a new block to the network, a time T has elapsed. The difficulty in receiving changes to D because it is reduced by one bit, so now it is equal to the difficulty for sending. At this time, the candidate block of N2 arrives at N3 which is at a distance of T time away. The relevance of the received block is the same as the difficulty for receiving, so N3 adds this block to its main chain and records the time it received. Since N2 has temporarily stored N1's block in the buffer, a time T has elapsed. N2 takes the block, which was received from N1, out of the buffer and checks once again for relevance. At this time, the relevance of the block is the same as the difficulty for receiving, so N1 also adds N2's block to its main chain and records the current time taken out from the buffer as the received time.

The following is an example that a chain is branched in the network which was originally assumed. The relevance of the next block created in N1 is smaller than the difficulty, D, for sending. N1 waits to receive blocks created by other nodes. Each relevance of the next blocks created in N2 and N3 has the same D value as the difficulty. Because both blocks satisfy the difficulty, the two nodes each add their own block to their main chain and send them to the network. One chain branch is divided again into two branches. N1 receives the adjacent N2's block first. The relevance of the received block is equal to D which is the relevance for sending, but it is smaller than D + 1 which is the difficulty for receiving, so N1 temporarily stores this block in its buffer. A time T has elapsed at N1. The difficulty in receiving changes to D because it is reduced by one bit, so now it is equal to the difficulty for sending. At this time, the N3's block arrives at N1 which is at a distance of T time away, and the relevance of the received block is the same as the difficulty for receiving, so N1 adds the N3's block to its main chain. Since N1 has temporarily stored the N2's block in the buffer, a time T has elapsed. Since the relevance of the N2's block is the same as the difficulty for receiving, N1 takes the N2's block out of the buffer and checks for relevance. The relevance of the blocks between N2 and N3 is the same, and N1 has received the N2's block first, but the N3's block was added to the N1's chain first, so the N3's block is left on the N1's main chain.

Nodes with the same main chain have the same average relevance, but the average transmission time is different in all nodes. In the above network, one zone transmission time T, rather than the zone transmission time of each node, was used to simplify the example, but it actually works so in the real world. Average transmission times of all nodes among adjacent zones are not exactly the same, but they do not make much difference.

When the blocks of N2 and N3 have the same relevance, N1 selected the N3's block in the adjacent zone, not the N2's block in the same zone. This is an example that the decrease in localization worked as intended. When the time distance between N2 and N1 is T * 0.1 and the time distance between N3 and N1 is T + ( T * 0.3 ), N1 will select N2's block and this also corresponds to the designed logic. However, even if the time distance between N2 and N1 is T * 0.1 and the time distance between N3 and N1 is T * 0.9, N1 will still select N2's block. Supposing that N3 is a little bit further away than N2 but N3 is also in the same zone, the localization has not been reduced when analyzed based on this zone alone. However, because this algorithm divides the entire network into zones of uniform proportion, the above situation corresponds to a probabilistic error case.

Most functional parts in this algorithm operate probabilistically. The times at which each node received the same previous candidate block are also different. In these situations, the first approach uses a simple method to place the difference in a dichotomous way. On the network, there are many other nodes, whose distances to N2 and N3 are separated by the zone transmission time, in addition to N1. For each of these nodes, the decrease in localization works relatively. We can think of a network that all nodes are uniformly distributed on the surface of the sphere, with their respective transmission times used for each distance. When operated on a network with only two zones with a branch quotient of 2, the decrease in localization works based on half the area of the entire network. The decrease in localization works most effectively when two nodes that can issue the next block are placed on each antipodal point on the surface of a sphere. In this case, the branching for a branch occasionally happens in the probabilistic error range. When there are only two zones in competition, the consensus is completed once one block and another block meet. In this algorithm, the node that will issue the next block is selected decisively by the algorithm based on random numbers with a uniform distribution. As a result, the dichotomous approach to the decrease in localization works effectively over a continuous period of time. What we have seen so far is not a complete elimination of localization but a probabilistic reduction. Other techniques to reduce localization will be used in other detailed designs of the algorithm also.

When the network grows larger as the nodes of the other zones are added one by one to the network originated from the first node, the average transmission time and the difficulty corresponding to the number of nodes generally increase together. However, the two values ​​are not always proportional. Depending on how the network grows, the average transmission time may decrease. When this consensus algorithm is operated as a public blockchain, the quality levels of each country's information network are different. Also, in this consensus algorithm, so many low-cost nodes with each proprietary information are owned by one individual that zones with very small average transmission time may be formed. Furthermore, a pool of multiple proprietary informations may be run on a single high-performance device. However, even in this case, there is no additional benefit from profits, due to the localization such as the case of PoW, and only profits proportional to the expense are made, so it can be accepted as a legitimate individual effort. In addition, methods to link the proprietary information with the real node or owner can be controlled according to the characteristics of the proprietary information and can also be considered in the implementation phase of the anonymous peer-to-peer network. The chain of this algorithm contains information about the entire network during the entire time. Regarding the network information contained in the candidate block chain, the closer to the leader block, the earlier the time, and the farther from the leader block, the more recent the time. Similarly, the closer to the leader block, the more wide the area, and the farther from the leader block, the more local the area. Using this information, which can be obtained from the chain, we can track how the network status changes. By statistically analyzing the variation, one chain stream can be divided into segments, and it allows each local network with a different physical environment to operate with different base values. However, this uneven network environment can lead to a wider localization by groups of zones. This is also handled by the algorithm and is covered in the next issue document on the convergence of the branched chains.

The time performance of the chain is the issuance speed of the authentication block, and the performance of the consensus algorithm is measured as the number of transactions per second, which is calculated by multiplying the number of authentication blocks issued per second by the number of ledgers included per block. In this algorithm, after one candidate block that was the leader block is consumed as one authentication block, as long as only one new candidate block is added to the chain, the threshold for the next leader block can be satisfied according to circumstances, and the next authentication block can be issued. One new candidate block can be issued based on the average transmission time of a zone as a unit of time, and one new authentication block can be issued at this time interval. When the average transmission time in the zone with the leader block is 1 second, this algorithm will have a TPS that is about 200 times higher than PoW in which the authentication is issued once every 10 minutes. When a smaller difficulty is used so that the average transmission time in the zone is about 1 millisecond, it will have a TPS that is about 200,000 times higher than PoW. However, it is not yet a step to say that this algorithm has a certain TPS as a performance value. A system for the basic consensus has been being designed, but the method of managing the authentication of the ledger, such as the size of the basic block or the structure of the merkle tree, has not yet been defined. Early implementations will probably follow the methods of other blockchains that are already in use. Considering the speed at which only one authentication block is issued, PoW is not only different from the methodology of this algorithm, but also can not be compared. This algorithm satisfies all the functional requirements for the blockchain and can be compared with algorithms with a DAG structure in terms of performance. However, when one authentication block is issued in this algorithm, as much effort as one block is issued in PoW is required. In the case of an effort of PoW, it takes 10 minutes for a block to be issued, but in this algorithm, even in small cases, it takes several hours until the newly added candidate block becomes a leader block satisfying the threshold. In the case of PoW in which most efforts have an indirect effect but do not directly cause change on information, only the effort of one node creates value and the efforts of all other nodes are discarded as useless, but in this algorithm, the system continues by the converging efforts of all nodes. In terms of the amount of effort involved in a block, one block in this algorithm is created by a considerable amount of effort that can not be compared with a block of PoW. As such, whereas it takes a lot of effort and time for one block, authentication is issued very quickly. Although expensive equipments for fast hashing are not required, all nodes must be connected to the network at all times and must be able to process the information of the chain continuously transmitted from the network in order to be synchronized with the current whole chain information.

I have tried to contain enough content so that anyone could easily try to implement the code for a situation where a block and a block meet, but not all the necessary content is contained. It was not easy to explain the probabilistic concept in writing, and also there was not enough time to put in a deep content. Due to personal reasons, I can not concentrate on this project yet, so this article is somewhat unobtrusive or ambiguous, and also there may be some misinformation. Regarding this issue document, I would like to write the rest of this content which I could not write because of lack of time, in additional documents as much as I can. I have just begun to write down the details of the design that was only in my head, so there may be some incorrect logic in parts such as probabilistic estimation. I had taken classes in information science related to security at the time of my master's degree, but I did not major in probability theory or network. By the voluntary participation of the people who are interested in the consensus algorithm itself or another possibility of the blockchain, regardless of whether they are major or not, I hope the algorithm will develop. So far, this algorithm has been being developed as a research project, but I hope it will have an opportunity to be implemented. The next issue document will show how to converge the branched chains. I can not be sure when it will be written because of my relaxed personality. However, the convergence of the chain should first be explained so that the whole algorithm will look a bit, so if possible it would be written as long as time permits.