994

994. Rotting Oranges (Medium)

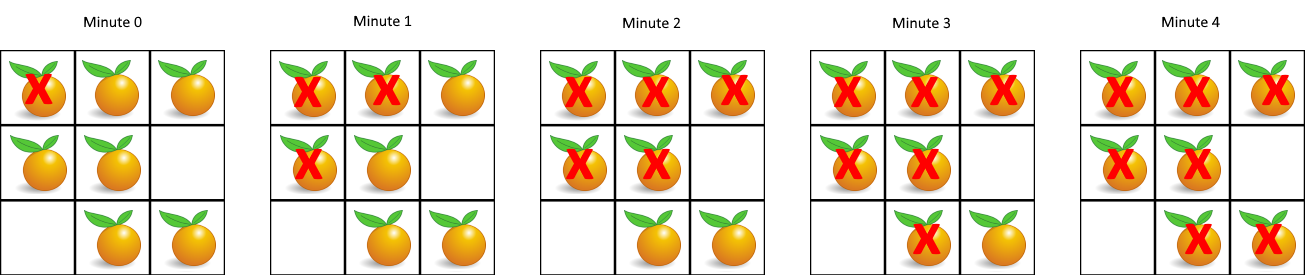
You are given an m x n grid where each cell can have one of three values:

• 0 representing an empty cell,
• 1 representing a fresh orange, or
• 2 representing a rotten orange.

Every minute, any fresh orange that is 4-directionally adjacent to a rotten orange becomes rotten.

Return the minimum number of minutes that must elapse until no cell has a fresh orange. If this is impossible, return -1.

 

Example 1:

Input: grid = [[2,1,1],[1,1,0],[0,1,1]]
Output: 4

Example 2:

Input: grid = [[2,1,1],[0,1,1],[1,0,1]]
Output: -1
Explanation: The orange in the bottom left corner (row 2, column 0) is never rotten, because rotting only happens 4-directionally.

Example 3:

Input: grid = [[0,2]]
Output: 0
Explanation: Since there are already no fresh oranges at minute 0, the answer is just 0.

 

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 10
• grid[i][j] is 0, 1, or 2.

Companies:
Amazon, Microsoft, Oracle, Google, Apple, Facebook, Bloomberg, Walmart Labs, Samsung, VMware

Related Topics:
Array, Breadth-First Search, Matrix

Similar Questions:

• Walls and Gates (Medium)

Solution 1. BFS

// OJ: https://leetcode.com/problems/rotting-oranges/
// Author: github.com/lzl124631x
// Time: O(MN)
// Space: O(MN)
class Solution {
public:
    int orangesRotting(vector<vector<int>>& A) {
        queue<pair<int, int>> q;
        int M = A.size(), N = A[0].size(), step = 0, dirs[4][2] = {{0,1},{0,-1},{1,0},{-1,0}};
        for (int i = 0; i < M; ++i) {
            for (int j = 0; j < N; ++j) {
                if (A[i][j] == 2) q.emplace(i, j);
            }
        }
        while (q.size()) {
            for (int cnt = q.size(); cnt--;) {
                auto [x, y] = q.front();
                q.pop();
                for (auto &[dx, dy] : dirs) {
                    int a = x + dx, b = y + dy;
                    if (a < 0 || a >= M || b < 0 || b >= N || A[a][b] != 1) continue;
                    A[a][b] = 2;
                    q.emplace(a, b);
                }
            }
            step++;
        }
        for (auto &row : A) {
            for (int x : row) {
                if (x == 1) return -1;
            }
        }
        return max(0, step - 1);
    }
};