790

790. Domino and Tromino Tiling (Medium)

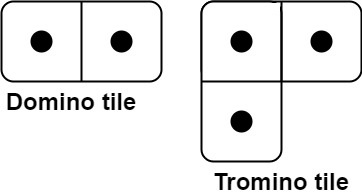
You have two types of tiles: a 2 x 1 domino shape and a tromino shape. You may rotate these shapes.

Given an integer n, return the number of ways to tile an 2 x n board. Since the answer may be very large, return it modulo 109 + 7.

In a tiling, every square must be covered by a tile. Two tilings are different if and only if there are two 4-directionally adjacent cells on the board such that exactly one of the tilings has both squares occupied by a tile.

 

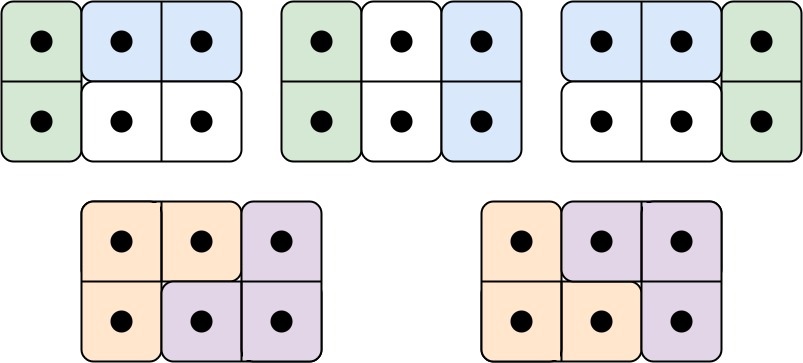
Example 1:

Input: n = 3
Output: 5
Explanation: The five different ways are show above.

Example 2:

Input: n = 1
Output: 1

 

Constraints:

• 1 <= n <= 1000

Companies:
Adobe

Related Topics:
Dynamic Programming

Solution 1. DP

Let dp[i][j] be the number of ways to tile to the i-th column in the first row and j-th column in the second row. The anwer is dp[n][n]

There are only 3 possible cases:

• dp[i][i]
• dp[i][i-1]
• dp[i-1][i]

Since dp[i][i-1] and dp[i-1][i] are symmetrical, we only need to calculate one of them.

For dp[i][i], there are 4 cases to get to it:

1. dp[i-1][i-1] when we put a vertical bar at the end
2. dp[i-1][i-2] when we put a ┛ at the end
3. dp[i-2][i-1] when we put a ┓ at the end
4. dp[i-2][i-2] when we put two horizontal bars at the end

After merging case 2 and 3, we get:

dp[i][i] = dp[i-1][i-1] + dp[i-1][i-2] * 2 + dp[i-2][i-2]

For dp[i][i-1], there are 2 cases:

1. dp[i-2][i-1] when we put a horizontal bar in the first row at the end
2. dp[i-2][i-2] when we put a ┏ at the end

Since dp[i-1][i-2] = dp[i-1][i-2], we can use dp[i-1][i-2] instead in case 1 so that we always only need to compute dp[i][i-1].

dp[i][i-1] = dp[i-1][i-2] + dp[i-2][i-2]

The trivial case is dp[0][0] = 1.

In the implementation, since we need to access i - 2, I'll offset the dp values by one so that I don't need to check i - 2 >= 0.

// OJ: https://leetcode.com/problems/domino-and-tromino-tiling/
// Author: github.com/lzl124631x
// Time: O(N)
// Space: O(N^2)
class Solution {
public:
    int numTilings(int n) {
        long mod = 1e9 + 7;
        vector<vector<long>> dp(n + 2, vector<long>(n + 2));
        dp[1][1] = 1;
        for (int i = 2; i <= n + 1; ++i) {
            dp[i][i] = (dp[i - 1][i - 1] + dp[i - 1][i - 2] * 2 + dp[i - 2][i - 2]) % mod;
            dp[i][i - 1] = (dp[i - 1][i - 2] + dp[i - 2][i - 2]) % mod;
        }
        return dp[n + 1][n + 1];
    }
};

Since dp[i][i] and dp[i][i-1] only depends on dp[i-1][i-1], dp[i-2][i-2], dp[i-1][i-2], we can reduce the space complexity to O(1).

// OJ: https://leetcode.com/problems/domino-and-tromino-tiling/
// Author: github.com/lzl124631x
// Time: O(N)
// Space: O(1)
class Solution {
public:
    int numTilings(int n) {
        long mod = 1e9 + 7, dp11 = 1, dp12 = 0, dp22 = 0;
        for (int i = 1; i <= n; ++i) {
            int dp00 = (dp11 + dp22 + dp12 * 2) % mod;
            int dp01 = (dp22 + dp12) % mod;
            dp22 = dp11;
            dp11 = dp00;
            dp12 = dp01;
        }
        return dp11;
    }
};