Given an m x n binary matrix mat, return the distance of the nearest 0 for each cell.
The distance between two adjacent cells is 1.
Example 1:
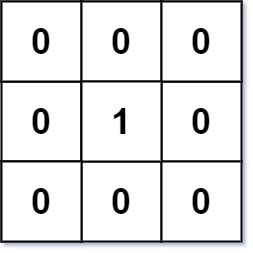
Input: mat = [[0,0,0],[0,1,0],[0,0,0]] Output: [[0,0,0],[0,1,0],[0,0,0]]
Example 2:
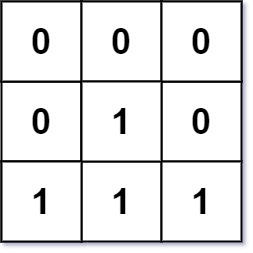
Input: mat = [[0,0,0],[0,1,0],[1,1,1]] Output: [[0,0,0],[0,1,0],[1,2,1]]
Constraints:
m == mat.lengthn == mat[i].length1 <= m, n <= 1041 <= m * n <= 104mat[i][j]is either0or1.- There is at least one
0inmat.
Companies: Microsoft, Google, Amazon
Related Topics:
Array, Dynamic Programming, Breadth-First Search, Matrix
Similar Questions:
- Shortest Path to Get Food (Medium)
- Minimum Operations to Remove Adjacent Ones in Matrix (Hard)
- Difference Between Ones and Zeros in Row and Column (Medium)
// OJ: https://leetcode.com/problems/01-matrix/
// Author: github.com/lzl124631x
// Time: O(MN)
// Space: O(MN)
class Solution {
public:
vector<vector<int>> updateMatrix(vector<vector<int>>& A) {
int M = A.size(), N = A[0].size(), dirs[4][2] = {{0,1},{0,-1},{1,0},{-1,0}};
vector<vector<int>> ans(M, vector<int>(N, INT_MAX));
queue<pair<int, int>> q;
for (int i = 0; i < M; ++i) {
for (int j = 0; j < N; ++j) {
if (A[i][j] == 0) {
q.emplace(i, j);
ans[i][j] = 0;
}
}
}
while (q.size()) {
int cnt = q.size();
while (cnt--) {
auto [x, y] = q.front();
q.pop();
for (auto &[dx, dy] : dirs) {
int a = x + dx, b = y + dy;
if (a < 0 || a >= M || b < 0 || b >= N || ans[a][b] != INT_MAX) continue;
ans[a][b] = 1 + ans[x][y];
q.emplace(a, b);
}
}
}
return ans;
}
};// OJ: https://leetcode.com/problems/01-matrix/
// Author: github.com/lzl124631x
// Time: O(MN)
// Space: O(1) if in-place computation is allowed; otherwise O(MN)
class Solution {
public:
vector<vector<int>> updateMatrix(vector<vector<int>>& A) {
int M = A.size(), N = A[0].size();
for (int i = 0; i < M; ++i) {
for (int j = 0; j < N; ++j) {
if (A[i][j]) A[i][j] = 0x3f3f3f3f;
}
}
for (int i = 0; i < M; ++i) {
for (int j = 0; j < N; ++j) {
A[i][j] = min({ A[i][j], i - 1 >= 0 ? A[i - 1][j] + 1 : INT_MAX, j - 1 >= 0 ? A[i][j - 1] + 1 : INT_MAX });
}
}
for (int i = M - 1; i >= 0; --i) {
for (int j = N - 1; j >= 0; --j) {
A[i][j] = min({ A[i][j], i + 1 < M ? A[i + 1][j] + 1 : INT_MAX, j + 1 < N ? A[i][j + 1] + 1 : INT_MAX });
}
}
return A;
}
};