You are given a 2D matrix grid of size m x n. In one operation, you can change the value of any cell to any non-negative number. You need to perform some operations such that each cell grid[i][j] is:
- Equal to the cell below it, i.e.
grid[i][j] == grid[i + 1][j](if it exists). - Different from the cell to its right, i.e.
grid[i][j] != grid[i][j + 1](if it exists).
Return the minimum number of operations needed.
Example 1:
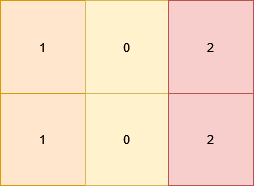
Input: grid = [[1,0,2],[1,0,2]]
Output: 0
Explanation:
All the cells in the matrix already satisfy the properties.
Example 2:
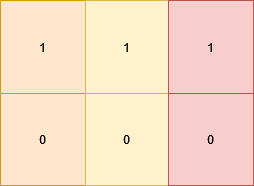
Input: grid = [[1,1,1],[0,0,0]]
Output: 3
Explanation:
The matrix becomes [[1,0,1],[1,0,1]] which satisfies the properties, by doing these 3 operations:
- Change
grid[1][0]to 1. - Change
grid[0][1]to 0. - Change
grid[1][2]to 1.
Example 3:
Input: grid = [[1],[2],[3]]
Output: 2
Explanation:
There is a single column. We can change the value to 1 in each cell using 2 operations.
Constraints:
1 <= n, m <= 10000 <= grid[i][j] <= 9
Similar Questions:
Hints:
- Use Hashing to store for each frequency of candies, how many times it occurs in each box.
- We can use dynamic programming.
// OJ: https://leetcode.com/problems/minimum-number-of-operations-to-satisfy-conditions
// Author: github.com/lzl124631x
// Time: O(MN)
// Space: O(N)
class Solution {
public:
int minimumOperations(vector<vector<int>>& A) {
int M = A.size(), N = A[0].size(), dp[1001][10] = {}, cnt[1001][10] = {};
memset(dp, 0x3f, sizeof(dp));
for (int j = 0; j < N; ++j) {
for (int i = 0; i < M; ++i) {
cnt[j][A[i][j]]++;
}
}
for (int i = 0; i < 10; ++i) dp[N - 1][i] = M - cnt[N - 1][i];
for (int j = N - 2; j >= 0; --j) {
for (int k = 0; k <= 9; ++k) {
for (int t = 0; t <= 9; ++t) {
if (k == t) continue;
dp[j][k] = min(dp[j][k], M - cnt[j][k] + dp[j + 1][t]);
}
}
}
int ans = INT_MAX;
for (int i = 0; i < 10; ++i) {
ans = min(ans, dp[0][i]);
}
return ans;
}
};