3044

3044. Most Frequent Prime (Medium)

You are given a m x n 0-indexed 2D matrix mat. From every cell, you can create numbers in the following way:

• There could be at most 8 paths from the cells namely: east, south-east, south, south-west, west, north-west, north, and north-east.
• Select a path from them and append digits in this path to the number being formed by traveling in this direction.
• Note that numbers are generated at every step, for example, if the digits along the path are 1, 9, 1, then there will be three numbers generated along the way: 1, 19, 191.

Return the most frequent prime number greater than 10 out of all the numbers created by traversing the matrix or -1 if no such prime number exists. If there are multiple prime numbers with the highest frequency, then return the largest among them.

Note: It is invalid to change the direction during the move.

 

Example 1:

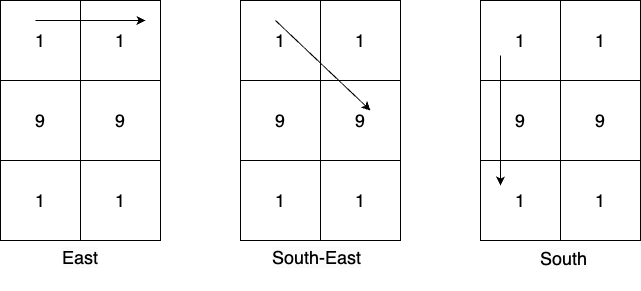
Input: mat = [[1,1],[9,9],[1,1]]
Output: 19
Explanation: 
From cell (0,0) there are 3 possible directions and the numbers greater than 10 which can be created in those directions are:
East: [11], South-East: [19], South: [19,191].
Numbers greater than 10 created from the cell (0,1) in all possible directions are: [19,191,19,11].
Numbers greater than 10 created from the cell (1,0) in all possible directions are: [99,91,91,91,91].
Numbers greater than 10 created from the cell (1,1) in all possible directions are: [91,91,99,91,91].
Numbers greater than 10 created from the cell (2,0) in all possible directions are: [11,19,191,19].
Numbers greater than 10 created from the cell (2,1) in all possible directions are: [11,19,19,191].
The most frequent prime number among all the created numbers is 19.

Example 2:

Input: mat = [[7]]
Output: -1
Explanation: The only number which can be formed is 7. It is a prime number however it is not greater than 10, so return -1.

Example 3:

Input: mat = [[9,7,8],[4,6,5],[2,8,6]]
Output: 97
Explanation: 
Numbers greater than 10 created from the cell (0,0) in all possible directions are: [97,978,96,966,94,942].
Numbers greater than 10 created from the cell (0,1) in all possible directions are: [78,75,76,768,74,79].
Numbers greater than 10 created from the cell (0,2) in all possible directions are: [85,856,86,862,87,879].
Numbers greater than 10 created from the cell (1,0) in all possible directions are: [46,465,48,42,49,47].
Numbers greater than 10 created from the cell (1,1) in all possible directions are: [65,66,68,62,64,69,67,68].
Numbers greater than 10 created from the cell (1,2) in all possible directions are: [56,58,56,564,57,58].
Numbers greater than 10 created from the cell (2,0) in all possible directions are: [28,286,24,249,26,268].
Numbers greater than 10 created from the cell (2,1) in all possible directions are: [86,82,84,86,867,85].
Numbers greater than 10 created from the cell (2,2) in all possible directions are: [68,682,66,669,65,658].
The most frequent prime number among all the created numbers is 97.

 

Constraints:

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 6
• 1 <= mat[i][j] <= 9

Hints:

• Use recursion to find all possible numbers for each cell and then check for prime.

Solution 1.

// OJ: https://leetcode.com/problems/most-frequent-prime
// Author: github.com/lzl124631x
// Time: O(MN * (M + N) * sqrt(9^max(M, N)))
// Space: O(MN)
class Solution {
    bool isPrime(int n) {
        if (n < 2) return false;
        for (int d = 2; d * d <= n; ++d) {
            if (n % d == 0) return false;
        }
        return true;
    }
public:
    int mostFrequentPrime(vector<vector<int>>& A) {
        int M = A.size(), N = A[0].size();
        unordered_map<int, int> freqs;
        for (int i = 0; i < M; ++i) {
            for (int j = 0; j < N; ++j) {
                for (int dx = -1; dx <= 1; ++dx) {
                    for (int dy = -1; dy <= 1; ++dy) {
                        if (dx == 0 && dy == 0) continue;
                        int x = i, y = j, n = 0;
                        while (x >= 0 && x < M && y >= 0 && y < N) {
                            n = n * 10 + A[x][y];
                            if (n > 10 && isPrime(n)) {
                                freqs[n]++;
                            }
                            x += dx;
                            y += dy;
                        }
                    }
                }
            }
        }
        int mxFreq = 0, ans = -1;
        for (auto &[n, f] : freqs) {
            if (f > mxFreq) ans = n, mxFreq = f;
            else if (f == mxFreq && n > ans) ans = n;
        }
        return ans;
    }
};