2876

2876. Count Visited Nodes in a Directed Graph (Hard)

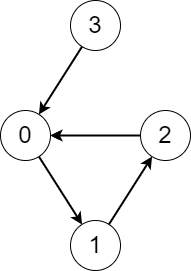
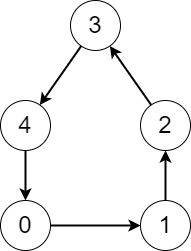
There is a directed graph consisting of n nodes numbered from 0 to n - 1 and n directed edges.

You are given a 0-indexed array edges where edges[i] indicates that there is an edge from node i to node edges[i].

Consider the following process on the graph:

• You start from a node x and keep visiting other nodes through edges until you reach a node that you have already visited before on this same process.

Return an array answer where answer[i] is the number of different nodes that you will visit if you perform the process starting from node i.

 

Example 1:

Input: edges = [1,2,0,0]
Output: [3,3,3,4]
Explanation: We perform the process starting from each node in the following way:
- Starting from node 0, we visit the nodes 0 -> 1 -> 2 -> 0. The number of different nodes we visit is 3.
- Starting from node 1, we visit the nodes 1 -> 2 -> 0 -> 1. The number of different nodes we visit is 3.
- Starting from node 2, we visit the nodes 2 -> 0 -> 1 -> 2. The number of different nodes we visit is 3.
- Starting from node 3, we visit the nodes 3 -> 0 -> 1 -> 2 -> 0. The number of different nodes we visit is 4.

Example 2:

Input: edges = [1,2,3,4,0]
Output: [5,5,5,5,5]
Explanation: Starting from any node we can visit every node in the graph in the process.

 

Constraints:

• n == edges.length
• 2 <= n <= 105
• 0 <= edges[i] <= n - 1
• edges[i] != i

Companies: BNY Mellon

Related Topics:
Dynamic Programming, Graph, Memoization

Hints:

• Consider if the graph was only one cycle, what will be the answer for each node?
• The actual graph will always consist of at least one cycle and some other nodes.
• Calculate the answer for nodes in cycles the same way as in hint 1. How do you calculate the answer for the remaining nodes?

Solution 1. DFS

// OJ: https://leetcode.com/problems/count-visited-nodes-in-a-directed-graph
// Author: github.com/lzl124631x
// Time: O(N)
// Space: O(N)
class Solution {
public:
    vector<int> countVisitedNodes(vector<int>& E) {
        int N = E.size();
        vector<int> dist(N, INT_MIN);
        function<int(int, int)> dfs = [&](int u, int d) {
            if (dist[u] != INT_MIN) { // this node is of state `visiting` or `visited`
                if (dist[u] < 0) { // this node is of state `visiting`, we've found a cycle
                    dist[u] -= d; // calculate the length of the cycle
                    return dist[u]; // we need to update remaining `dist[u]` elements with the length of the cycle
                }
                return 0;
            }
            dist[u] = d; // when visiting nodes, we mark them with negative depth
            int remaining = dfs(E[u], d - 1);
            if (remaining-- > 0) dist[u] = dist[E[u]]; // If remaining > 0, we are still in the cycle, the distances should be the same
            else dist[u] = dist[E[u]] + 1; // otherwise, we are out of cycle, the distance should be 1 plus E[u]'s distance
            return remaining;
        };
        for (int i = 0; i < N; ++i) {
            if (dist[i] != INT_MIN) continue;
            dfs(i, -1);
        }
        return dist;
    }
};