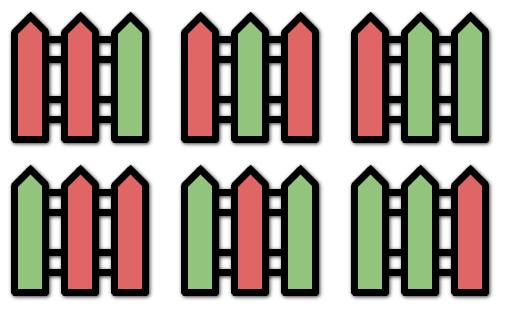
You are painting a fence of n posts with k different colors. You must paint the posts following these rules:
- Every post must be painted exactly one color.
- There cannot be three or more consecutive posts with the same color.
Given the two integers n and k, return the number of ways you can paint the fence.
Example 1:
Input: n = 3, k = 2 Output: 6 Explanation: All the possibilities are shown. Note that painting all the posts red or all the posts green is invalid because there cannot be three posts in a row with the same color.
Example 2:
Input: n = 1, k = 1 Output: 1
Example 3:
Input: n = 7, k = 2 Output: 42
Constraints:
1 <= n <= 501 <= k <= 105- The testcases are generated such that the answer is in the range
[0, 231 - 1]for the givennandk.
Companies:
JPMorgan
Related Topics:
Dynamic Programming
Similar Questions:
Let dp[i][j] be the number of different ways to paint the fence if we are using i fences and the last fence repeated j times. 1 <= i <= n, j = 1 or 2.
If j == 1, we can pick a different color (k - 1 options) as the previous ending color which might repeat once or twice. So dp[i][1] = (k-1) * (dp[i-1][1] + dp[i-1][2]).
If j == 2, the count must be the same as dp[i-1][1], i.e. dp[i][2] = dp[i-1][1].
So we have:
dp[i][1] = (k - 1) * (dp[i-1][1] + dp[i-1][2]) // pick another color (k - 1 choices)
dp[i][2] = dp[i-1][1]
Trivial cases:
dp[1][1] = k
dp[1][2] = 0
The answer is dp[n][1] + dp[n][2].
Since dp[i][j] is only dependent on dp[i-1][k], we can reduce the space complexity from n * 2 to 1 * 2.
// OJ: https://leetcode.com/problems/paint-fence/
// Author: github.com/lzl124631x
// Time: O(N)
// Space: O(1)
class Solution {
public:
int numWays(int n, int k) {
if (k == 1 && n >= 3) return 0;
int dp[2] = {k, 0};
for (int i = 1; i < n; ++i) {
int next[2] = {(k - 1) * (dp[0] + dp[1]), dp[0]};
swap(next, dp);
}
return dp[0] + dp[1];
}
};