2718

2718. Sum of Matrix After Queries (Medium)

You are given an integer n and a 0-indexed 2D array queries where queries[i] = [typei, indexi, vali].

Initially, there is a 0-indexed n x n matrix filled with 0's. For each query, you must apply one of the following changes:

• if typei == 0, set the values in the row with indexi to vali, overwriting any previous values.
• if typei == 1, set the values in the column with indexi to vali, overwriting any previous values.

Return the sum of integers in the matrix after all queries are applied.

 

Example 1:

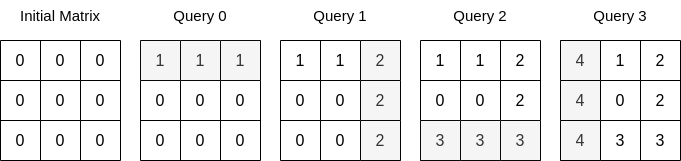
Input: n = 3, queries = [[0,0,1],[1,2,2],[0,2,3],[1,0,4]]
Output: 23
Explanation: The image above describes the matrix after each query. The sum of the matrix after all queries are applied is 23. 

Example 2:

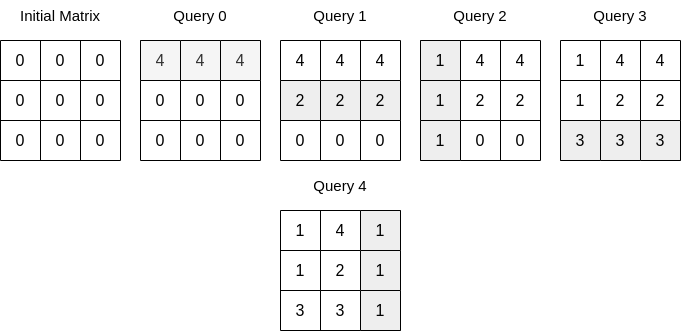
Input: n = 3, queries = [[0,0,4],[0,1,2],[1,0,1],[0,2,3],[1,2,1]]
Output: 17
Explanation: The image above describes the matrix after each query. The sum of the matrix after all queries are applied is 17.

 

Constraints:

• 1 <= n <= 104
• 1 <= queries.length <= 5 * 104
• queries[i].length == 3
• 0 <= typei <= 1
• 0 <= indexi < n
• 0 <= vali <= 105

Related Topics:
Array, Hash Table

Similar Questions:

• Range Sum Query 2D - Mutable (Hard)
• Range Addition II (Easy)

Hints:

• Process queries in reversed order, as the latest queries represent the most recent changes in the matrix.
• Once you encounter an operation on some row/column, no further operations will affect the values in this row/column. Keep track of seen rows and columns with a set.
• When operating on an unseen row/column, the number of affected cells is the number of columns/rows you haven’t previously seen.

Solution 1.

Intuition:

I first considered traversing the queries in order. When I meet queries writing to row/columns that have been written before, I need to overwrite the previous query. Also, assume the current query is writing to a row and there is no other query writing to the same row, to know to how many cells the current query writes, I need to know how many unique column queries after this query. If I also consider that there might be another row query writing to the same row as the current query, the problem becomes more complicated.

Here, I thought about traversing the queries in the reverse order. In this way, I don't need to do overwriting; I just need to check if a row/column has been written, and skip any earlier queries. Also, computing how many column queries are after the current row query is trivial now, we can simply count unique column queries we've seen so far.

Algorithm:

Traverse the queries in reverse order. Using a vector<unordered_set<int>> seen(2) to check if an index has been seen before.

If it has been seen before, skip this query.

Otherwise, seen[type].insert(index), and increase answer by (n - seen[1 - type].size()) * val.

// OJ: https://leetcode.com/problems/sum-of-matrix-after-queries
// Author: github.com/lzl124631x
// Time: O(Q)
// Space: O(min(N, Q))
class Solution {
public:
    long long matrixSumQueries(int n, vector<vector<int>>& Q) {
        long long ans = 0;
        vector<unordered_set<int>> seen(2);
        for (int i = Q.size() - 1; i >= 0; --i) {
            int type = Q[i][0], index = Q[i][1], val = Q[i][2];
            if (seen[type].count(index)) continue;
            seen[type].insert(index);
            ans += (n - seen[1 - type].size()) * val;
        }
        return ans;
    }
};

Using array can save a bit of time.

// OJ: https://leetcode.com/problems/sum-of-matrix-after-queries
// Author: github.com/lzl124631x
// Time: O(Q)
// Space: O(N)
class Solution {
public:
    long long matrixSumQueries(int n, vector<vector<int>>& Q) {
        long long ans = 0;
        bool seen[2][10000] = {};
        int cnt[2] = {};
        for (int i = Q.size() - 1; i >= 0; --i) {
            int type = Q[i][0], index = Q[i][1], val = Q[i][2];
            if (seen[type][index]) continue;
            seen[type][index] = true;
            cnt[type]++;
            ans += (n - cnt[1 - type]) * val;
        }
        return ans;
    }
};