2685

2685. Count the Number of Complete Components (Medium)

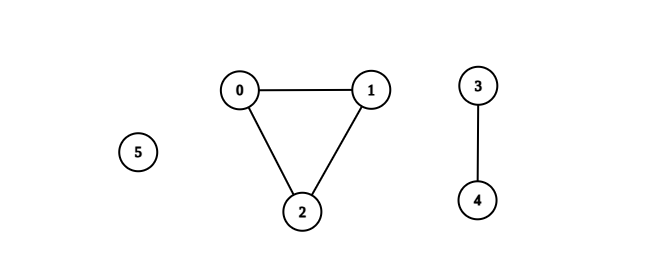
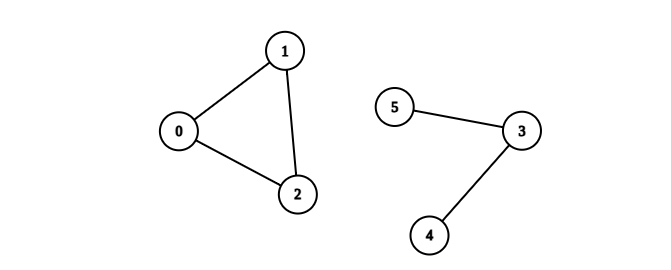
You are given an integer n. There is an undirected graph with n vertices, numbered from 0 to n - 1. You are given a 2D integer array edges where edges[i] = [ai, bi] denotes that there exists an undirected edge connecting vertices ai and bi.

Return the number of complete connected components of the graph.

A connected component is a subgraph of a graph in which there exists a path between any two vertices, and no vertex of the subgraph shares an edge with a vertex outside of the subgraph.

A connected component is said to be complete if there exists an edge between every pair of its vertices.

 

Example 1:

Input: n = 6, edges = [[0,1],[0,2],[1,2],[3,4]]
Output: 3
Explanation: From the picture above, one can see that all of the components of this graph are complete.

Example 2:

Input: n = 6, edges = [[0,1],[0,2],[1,2],[3,4],[3,5]]
Output: 1
Explanation: The component containing vertices 0, 1, and 2 is complete since there is an edge between every pair of two vertices. On the other hand, the component containing vertices 3, 4, and 5 is not complete since there is no edge between vertices 4 and 5. Thus, the number of complete components in this graph is 1.

 

Constraints:

• 1 <= n <= 50
• 0 <= edges.length <= n * (n - 1) / 2
• edges[i].length == 2
• 0 <= ai, bi <= n - 1
• ai != bi
• There are no repeated edges.

Related Topics:
Depth-First Search, Breadth-First Search, Graph

Similar Questions:

• Number of Connected Components in an Undirected Graph (Medium)

Solution 1.

// OJ: https://leetcode.com/problems/count-the-number-of-complete-components
// Author: github.com/lzl124631x
// Time: O(NlogN)
// Space: O(N)
class UnionFind {
    vector<int> id, size;
public:
    UnionFind(int n) : id(n), size(n, 1) {
        iota(begin(id), end(id), 0);
    }
    int find(int a) {
        return id[a] == a ? a : (id[a] = find(id[a]));
    }
    void connect(int a, int b) {
        int x = find(a), y = find(b);
        if (x == y) return;
        id[x] = y;
        size[y] += size[x];
    }
    int getSize(int a) { return size[find(a)]; }
};
class Solution {
public:
    int countCompleteComponents(int n, vector<vector<int>>& E) {
        vector<int> degree(n);
        UnionFind uf(n);
        for (auto &e : E) {
            int u = e[0], v = e[1];
            uf.connect(u, v);
            degree[u]++;
            degree[v]++;
        }
        unordered_map<int, int> cnt;
        for (int i = 0; i < n; ++i) {
            cnt[uf.find(i)] += degree[i];
        }
        int ans = 0;
        for (auto &[r, c] : cnt) {
            int sz = uf.getSize(r);
            ans += sz * (sz - 1) == c;
        }
        return ans;
    }
};