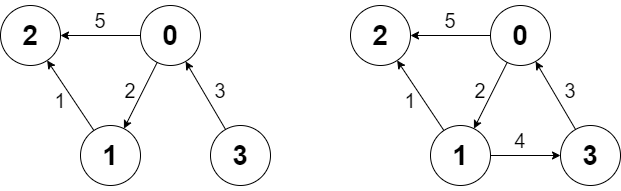
There is a directed weighted graph that consists of n nodes numbered from 0 to n - 1. The edges of the graph are initially represented by the given array edges where edges[i] = [fromi, toi, edgeCosti] meaning that there is an edge from fromi to toi with the cost edgeCosti.
Implement the Graph class:
Graph(int n, int[][] edges)initializes the object withnnodes and the given edges.addEdge(int[] edge)adds an edge to the list of edges whereedge = [from, to, edgeCost]. It is guaranteed that there is no edge between the two nodes before adding this one.int shortestPath(int node1, int node2)returns the minimum cost of a path fromnode1tonode2. If no path exists, return-1. The cost of a path is the sum of the costs of the edges in the path.
Example 1:
Input ["Graph", "shortestPath", "shortestPath", "addEdge", "shortestPath"] [[4, [[0, 2, 5], [0, 1, 2], [1, 2, 1], [3, 0, 3]]], [3, 2], [0, 3], [[1, 3, 4]], [0, 3]] Output [null, 6, -1, null, 6]Explanation Graph g = new Graph(4, [[0, 2, 5], [0, 1, 2], [1, 2, 1], [3, 0, 3]]); g.shortestPath(3, 2); // return 6. The shortest path from 3 to 2 in the first diagram above is 3 -> 0 -> 1 -> 2 with a total cost of 3 + 2 + 1 = 6. g.shortestPath(0, 3); // return -1. There is no path from 0 to 3. g.addEdge([1, 3, 4]); // We add an edge from node 1 to node 3, and we get the second diagram above. g.shortestPath(0, 3); // return 6. The shortest path from 0 to 3 now is 0 -> 1 -> 3 with a total cost of 2 + 4 = 6.
Constraints:
1 <= n <= 1000 <= edges.length <= n * (n - 1)edges[i].length == edge.length == 30 <= fromi, toi, from, to, node1, node2 <= n - 11 <= edgeCosti, edgeCost <= 106- There are no repeated edges and no self-loops in the graph at any point.
- At most
100calls will be made foraddEdge. - At most
100calls will be made forshortestPath.
Companies: Samsung
Related Topics:
Graph, Design, Heap (Priority Queue), Shortest Path
Similar Questions:
// OJ: https://leetcode.com/problems/design-graph-with-shortest-path-calculator
// Author: github.com/lzl124631x
// Time:
// Graph: O(N + E)
// addEdge: O(1)
// shortestPath: O(N + ElogE)
// Space: O(N + E)
class Graph {
vector<vector<pair<int, int>>> G;
int n;
public:
Graph(int n, vector<vector<int>>& E) : n(n), G(n) {
for (auto &e : E) G[e[0]].emplace_back(e[1], e[2]);
}
void addEdge(vector<int> e) {
G[e[0]].emplace_back(e[1], e[2]);
}
int shortestPath(int u, int v) {
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> pq; // cost, node
pq.emplace(0, u);
vector<int> d(n, INT_MAX);
d[u] = 0;
while (pq.size()) {
auto [cost, node] = pq.top();
pq.pop();
if (cost > d[node]) continue;
for (auto &[next, weight] : G[node]) {
if (d[next] > cost + weight) {
d[next] = cost + weight;
pq.emplace(d[next], next);
}
}
}
return d[v] == INT_MAX ? -1 : d[v];
}
};// OJ: https://leetcode.com/problems/design-graph-with-shortest-path-calculator
// Author: github.com/lzl124631x
// Time:
// Graph: O(E + N^3)
// addEdge: O(N^2)
// shortestPath: O(1)
// Space: O(N^2)
class Graph {
vector<vector<int>> dist;
int n;
public:
Graph(int n, vector<vector<int>>& E) : n(n), dist(n, vector<int>(n, 1e9)) {
for (int i = 0; i < n; ++i) dist[i][i] = 0;
for (auto &e : E) dist[e[0]][e[1]] = e[2];
for (int k = 0; k < n; ++k) { // Typical Floyd-Warshall algorithm. Use a middle node `k` to relax the min distance from `i` to `j`
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);
}
}
}
}
void addEdge(vector<int> e) {
if (e[2] >= dist[e[0]][e[1]]) return;
for (int i = 0; i < n; ++i) { // Use this edge to relax the min distance from `i` to `j`.
for (int j = 0; j < n; ++j) {
dist[i][j] = min(dist[i][j], dist[i][e[0]] + e[2] + dist[e[1]][j]);
}
}
}
int shortestPath(int u, int v) {
return dist[u][v] == 1e9 ? -1 : dist[u][v];
}
};