There is an undirected tree with n nodes labeled from 0 to n - 1. You are given the integer n and a 2D integer array edges of length n - 1, where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree. The root of the tree is the node labeled 0.
Each node has an associated value. You are given an array values of length n, where values[i] is the value of the ith node.
Select any two non-overlapping subtrees. Your score is the bitwise XOR of the sum of the values within those subtrees.
Return the maximum possible score you can achieve. If it is impossible to find two nonoverlapping subtrees, return 0.
Note that:
- The subtree of a node is the tree consisting of that node and all of its descendants.
- Two subtrees are non-overlapping if they do not share any common node.
Example 1:
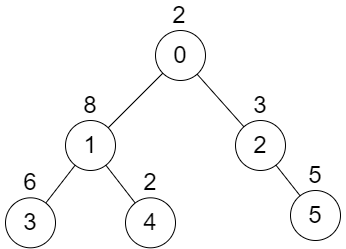
Input: n = 6, edges = [[0,1],[0,2],[1,3],[1,4],[2,5]], values = [2,8,3,6,2,5] Output: 24 Explanation: Node 1's subtree has sum of values 16, while node 2's subtree has sum of values 8, so choosing these nodes will yield a score of 16 XOR 8 = 24. It can be proved that is the maximum possible score we can obtain.
Example 2:
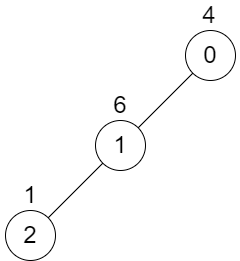
Input: n = 3, edges = [[0,1],[1,2]], values = [4,6,1] Output: 0 Explanation: There is no possible way to select two non-overlapping subtrees, so we just return 0.
Constraints:
2 <= n <= 5 * 104edges.length == n - 10 <= ai, bi < nvalues.length == n1 <= values[i] <= 109- It is guaranteed that
edgesrepresents a valid tree.
Related Topics:
Tree, Depth-First Search, Graph, Trie
Hints:
- Try to build the answer bit by bit from the most significant bit to the least significant.
- Use the Trie Data Structure to decide for each bit if it exists in the final answer.
Given a subtree sum, Trie can help us quickly find the maxXor.
But how do we exclude the nodes that are ancestors or descendent of the current node? I found that we can use a mix of pre-order and post-order traversal:
- First of all, we precompute the subtree sum of a node
uassum[u]. - Then, we do the mixed pre/post-order traversal.
- When visiting a node
u, we use Trie to calcuate the maxXor value corresponding tosum[u]. (This is the pre-order part) - We DFS to node
u's decendents. - Then, we add
sum[u]to the Trie. (This is the post-order part)
- When visiting a node
// OJ: https://leetcode.com/problems/maximum-xor-of-two-non-overlapping-subtrees
// Author: github.com/lzl124631x
// Time: O(N)
// Space: O(N)
struct TrieNode {
TrieNode *next[2] = {};
};
class Solution {
void addNumber(TrieNode *node, long long n) {
for (int i = 63; i >= 0; --i) {
long long b = n >> i & 1;
if (!node->next[b]) node->next[b] = new TrieNode();
node = node->next[b];
}
}
long long getMaxXor(TrieNode *node, long long n) {
long long ans = 0;
for (int i = 63; i >= 0; --i) {
long long b = n >> i & 1, r = 1 - b;
if (node->next[r]) node = node->next[r], ans |= (1LL << i);
else if (node->next[b]) node = node->next[b];
else return 0;
}
return ans;
}
public:
long long maxXor(int n, vector<vector<int>>& E, vector<int>& A) {
vector<vector<int>> G(n);
for (auto &e : E) {
int u = e[0], v = e[1];
G[u].push_back(v);
G[v].push_back(u);
}
TrieNode root;
unordered_map<int, long long> sum;
function<long long(int, int)> getSubTreeSum = [&](int u, int prev) -> long long {
long long ans = A[u];
for (int v : G[u]) {
if (v == prev) continue;
ans += getSubTreeSum(v, u);
}
return sum[u] = ans;
};
getSubTreeSum(0, -1);
long long ans = 0;
function<void(int, int)> dfs = [&](int u, int prev) {
ans = max(ans, getMaxXor(&root, sum[u]));
for (int v : G[u]) {
if (v == prev) continue;
dfs(v, u);
}
addNumber(&root, sum[u]);
};
dfs(0, -1);
return ans;
}
};