2428

2428. Maximum Sum of an Hourglass (Medium)

You are given an m x n integer matrix grid.

We define an hourglass as a part of the matrix with the following form:

Return the maximum sum of the elements of an hourglass.

Note that an hourglass cannot be rotated and must be entirely contained within the matrix.

 

Example 1:

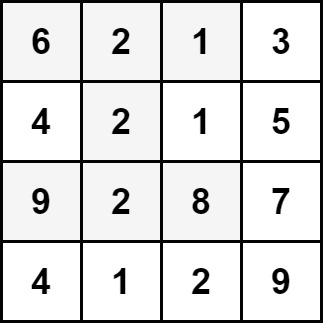
Input: grid = [[6,2,1,3],[4,2,1,5],[9,2,8,7],[4,1,2,9]]
Output: 30
Explanation: The cells shown above represent the hourglass with the maximum sum: 6 + 2 + 1 + 2 + 9 + 2 + 8 = 30.

Example 2:

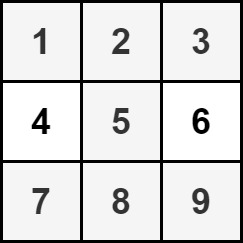
Input: grid = [[1,2,3],[4,5,6],[7,8,9]]
Output: 35
Explanation: There is only one hourglass in the matrix, with the sum: 1 + 2 + 3 + 5 + 7 + 8 + 9 = 35.

 

Constraints:

• m == grid.length
• n == grid[i].length
• 3 <= m, n <= 150
• 0 <= grid[i][j] <= 106

Companies: Nutanix

Related Topics:
Array, Matrix, Prefix Sum

Similar Questions:

• Matrix Block Sum (Medium)

Solution 1. Brute Force

// OJ: https://leetcode.com/problems/maximum-sum-of-an-hourglass
// Author: github.com/lzl124631x
// Time: O(MN)
// Space: O(1)
class Solution {
public:
    int maxSum(vector<vector<int>>& A) {
        int M = A.size(), N = A[0].size(), ans = 0;
        for (int i = 0; i <= M - 3; ++i) {
            for (int j = 0; j <= N - 3; ++j) {
                ans = max(ans, A[i][j] + A[i][j + 1] + A[i][j + 2] + A[i + 1][j + 1] + A[i + 2][j] + A[i + 2][j + 1] + A[i + 2][j + 2]);
            }
        }
        return ans;
    }
};