2360

2360. Longest Cycle in a Graph (Hard)

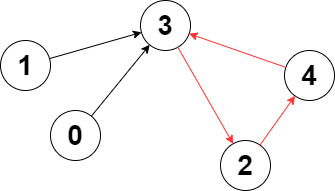
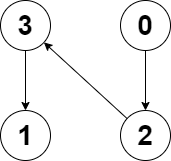
You are given a directed graph of n nodes numbered from 0 to n - 1, where each node has at most one outgoing edge.

The graph is represented with a given 0-indexed array edges of size n, indicating that there is a directed edge from node i to node edges[i]. If there is no outgoing edge from node i, then edges[i] == -1.

Return the length of the longest cycle in the graph. If no cycle exists, return -1.

A cycle is a path that starts and ends at the same node.

 

Example 1:

Input: edges = [3,3,4,2,3]
Output: 3
Explanation: The longest cycle in the graph is the cycle: 2 -> 4 -> 3 -> 2.
The length of this cycle is 3, so 3 is returned.

Example 2:

Input: edges = [2,-1,3,1]
Output: -1
Explanation: There are no cycles in this graph.

 

Constraints:

• n == edges.length
• 2 <= n <= 105
• -1 <= edges[i] < n
• edges[i] != i

Companies: Juspay, Microsoft

Related Topics:
Depth-First Search, Graph, Topological Sort

Similar Questions:

• Strange Printer II (Hard)
• Minimum Number of Operations to Sort a Binary Tree by Level (Medium)
• Shortest Cycle in a Graph (Hard)

Solution 1.

• Similar to topological sort, keep removing nodes with 0 indegrees.
• For the remaining nodes, DFS to get the depth

// OJ: https://leetcode.com/problems/longest-cycle-in-a-graph
// Author: github.com/lzl124631x
// Time: O(N)
// Space: O(N)
class Solution {
public:
    int longestCycle(vector<int>& E) {
        int N = E.size(), ans = -1;
        vector<int> indegree(N), depth(N);
        for (int i = 0; i < N; ++i) {
            if (E[i] == -1) continue;
            indegree[E[i]]++;
        }
        queue<int> q;
        for (int i = 0; i < N; ++i) {
            if (indegree[i] == 0) q.push(i);
        }
        while (q.size()) {
            int u = q.front();
            q.pop();
            depth[u] = -1; // depth[u] == -1 means that this node u is not in a cycle.
            if (E[u] != -1 && --indegree[E[u]] == 0) q.push(E[u]);
        }
        function<int(int, int)> dfs = [&](int i, int d) {
            if (depth[i] == -1) return -1; 
            depth[i] = d;
            if (depth[E[i]]) return depth[i];
            return depth[i] = dfs(E[i], 1 + d);
        };
        for (int i = 0; i < N; ++i) {
            ans = max(ans, dfs(i, 1));
        }
        return ans;
    }
};