2316

2316. Count Unreachable Pairs of Nodes in an Undirected Graph (Medium)

You are given an integer n. There is an undirected graph with n nodes, numbered from 0 to n - 1. You are given a 2D integer array edges where edges[i] = [ai, bi] denotes that there exists an undirected edge connecting nodes ai and bi.

Return the number of pairs of different nodes that are unreachable from each other.

 

Example 1:

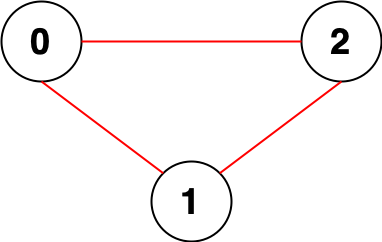
Input: n = 3, edges = [[0,1],[0,2],[1,2]]
Output: 0
Explanation: There are no pairs of nodes that are unreachable from each other. Therefore, we return 0.

Example 2:

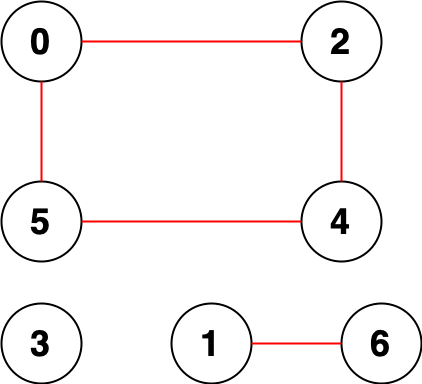
Input: n = 7, edges = [[0,2],[0,5],[2,4],[1,6],[5,4]]
Output: 14
Explanation: There are 14 pairs of nodes that are unreachable from each other:
[[0,1],[0,3],[0,6],[1,2],[1,3],[1,4],[1,5],[2,3],[2,6],[3,4],[3,5],[3,6],[4,6],[5,6]].
Therefore, we return 14.

 

Constraints:

• 1 <= n <= 105
• 0 <= edges.length <= 2 * 105
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• There are no repeated edges.

Companies: Amazon

Related Topics:
Depth-First Search, Breadth-First Search, Union Find, Graph

Similar Questions:

• Number of Islands (Medium)

Solution 1. Union Find

// OJ: https://leetcode.com/problems/count-unreachable-pairs-of-nodes-in-an-undirected-graph
// Author: github.com/lzl124631x
// Time: O(NlogN * K^2) where K is the number of unique graph component sizes
// Space: O(N)
class UnionFind {
    vector<int> id, size;
public:
    UnionFind(int N) : id(N), size(N, 1) {
        iota(begin(id), end(id), 0);
    }
    int find(int a) {
        return id[a] == a ? a : (id[a] = find(id[a]));
    }
    void connect(int a, int b) {
        int p = find(a), q = find(b);
        if (p == q) return;
        id[q] = p;
        size[p] += size[q];
    }
    int getSize(int a) {
        return size[find(a)];
    }
};
class Solution {
public:
    long long countPairs(int n, vector<vector<int>>& E) {
        UnionFind uf(n);
        for (auto &e : E) uf.connect(e[0], e[1]);
        unordered_set<int> seen;
        long long ans = 0;
        unordered_map<int, int> cnt;
        for (int i = 0; i < n; ++i) {
            int r = uf.find(i);
            if (seen.count(r)) continue;
            seen.insert(r);
            cnt[uf.getSize(r)]++;
        }
        for (auto a = cnt.begin(); a != cnt.end(); ++a) {
            long long sa = a->first, ca = a->second;
            ans += sa * sa * ca * (ca - 1) / 2;
            for (auto b = next(a); b != cnt.end(); ++b) {
                long long sb = b->first, cb = b->second;
                ans += sa * sb * ca * cb;
            }
        }
        return ans;
    }
};